Verkettung von drei Geradenspiegelungen SoSe 12: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=== Verkettung von drei Geradenspiegelungen === Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei Ge…“) |
Nelson (Diskussion | Beiträge) (→Satz X.1:) |
||
| (6 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
:Die Verkettung von drei Geradenspiegelungen <math>S_{a}\cir S_{b} \cir S_{c}</math> an zueinander parallelen Geraden ''a'', ''b'' und ''c'' ist eine Geradenspiegelung an einer Geraden ''d'' mit <math>d || a </math> und <math>\left| ab \right| =\left| dc \right| </math>.<br /> | :Die Verkettung von drei Geradenspiegelungen <math>S_{a}\cir S_{b} \cir S_{c}</math> an zueinander parallelen Geraden ''a'', ''b'' und ''c'' ist eine Geradenspiegelung an einer Geraden ''d'' mit <math>d || a </math> und <math>\left| ab \right| =\left| dc \right| </math>.<br /> | ||
Beweis:<br /><br /> | Beweis:<br /><br /> | ||
| + | muss die gerade d nicht noch genauer beschrieben werden? es gibt doch zwei zu c parallele geraden die den gleichen abstand (wie die gerade a und b) haben--[[Benutzer:Studentin|Studentin]] 23:08, 1. Jul. 2012 (CEST)<br /> | ||
| + | mmh, gut mitgedacht - was meinen die Anderen?--[[Benutzer:Schnirch|Schnirch]] 15:29, 2. Jul. 2012 (CEST) | ||
| + | seh ich genauso, das problem ergibt sich unten bei den Winkeln ebenso, oder nicht? [[Benutzer:Nelson|Nelson]] 14:23, 6. Jul. 2012 (CEST) | ||
| + | wobei die Winkel unten gerichtet sind, also doch nicht... [[Benutzer:Nelson|Nelson]] 14:30, 6. Jul. 2012 (CEST) | ||
=====Satz X.2: ===== | =====Satz X.2: ===== | ||
| − | :Die Verkettung von drei Geradenspiegelungen <math>S_{a}\cir S_{b} \cir S_{c}</math>, an drei Geraden ''a'', ''b'' und ''c'' die sich in einem Punkt ''S'' schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse ''d'', die durch den Punkt ''S'' verläuft mit <math>\angle ab = \angle dc </math>.<br /> | + | :Die Verkettung von drei Geradenspiegelungen <math>S_{a}\cir S_{b} \cir S_{c}</math>, an drei Geraden ''a'', ''b'' und ''c'' die sich in einem Punkt ''S'' schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse ''d'', die durch den Punkt ''S'' verläuft mit <math>\left|\angle ab\right| = \left|\angle dc\right| </math>.<br /> |
| + | Beweis:<br /><br /> | ||
| + | |||
| + | =====Definition X.1 (Schub- oder Gleitspiegelung)===== | ||
| + | Eine Schub- oder Gleitspiegelung ist eine Abbildung, die bei der Verkettung dreier Geradenspiegelungen <math>S_{a}\cir S_{b} \cir S_{c}</math> entsteht, wenn die zwei Geraden ''a'' und ''b'' parallel zueinander und die dritte Gerade ''c'' senkrecht dazu steht.<br /><br /> | ||
| + | Experimentieren Sie mit der nachfolgenden GeoGebra-Applikation. Welche Eigenschaften der Schubspiegelung entdecken Sie?<br /><br /> | ||
| + | <ggb_applet width="621" height="538" version="4.0" ggbBase64="UEsDBBQACAAIAHSn3kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAHSn3kAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VlRb9s4En7u/gpCz7UtUhQlFXYX2+wWVyC7LZDe4XBvlETb3MiiTqQdO9gff0NSkuUkTZM2aXtrJKEojmY438x8Qznzn/ebCu1Eq6WqFwGehgESdaFKWa8WwdYsJ2nw8+uf5iuhViJvOVqqdsPNIqBWUpaLgKR5GjOcT7gQ+YQuhZjkueATxrMyTbHgPIwChPZavqrVH3wjdMMLcVGsxYafq4IbZ3htTPNqNru6upr2pqaqXc1Wq3y612WAYJu1XgTdxStQd/LQVeTESRji2b9/P/fqJ7LWhteFCJB1YStf//RifiXrUl2hK1ma9SJgJAvQWsjVGnxiIfg0s0INANKIwsid0PDoaOp8NpsmcGK8tusv/BWqBncCVMqdLEW7CMJphJOMxSGJUppECUsDpFopatPJ4s7mrNc230lx5dXaK2eRBsgoVeXcakR//YVISEL00g7YDwQGxvxS6O+FkR+IH6gfYi9D/ePUi1IvQ70MhYjtpJZ5JRbBklcaEJT1soXoDXNtDpVw++luHL3HL8EnLa9BOLKQesjhfhi+tL+A80vaYz1yEo+smnb7SKO9SUbww02Sr3I06m2Su9wk8SfcZPcY9X4/xE8cj2yCKffjfm9ZjO5z86ZFP/86g4x+Exfns75U5l11IL22sl32GLHRtl6iDMWZTXuMYqgNlkCWxwhnMCQEQTUgHCMawxSniNkxQVECCxRFKEVWDkfIFUecwh+aOGUMxaDM3k2gJhEGQxTFEcKupiiCSkKuLqFGSQQScYxieMiax8SqiBiiDGZRiijs0ZZkgkEwggdhDuYJijCK7MM4QYQhZvVhakudpXbroJIgFiKGrUKoaqhoX80gn6LIesM6uGTdbM0JRMWm7C+NaoZYgDTw0ZH1PD+dkOKLecVzUUGfuLCRRGjHK1sRztBS1Qb1QST+3qrlzVoW+kIYA09p9Cff8XNuxP4tSOvetpMtVK0/tMqcqWq7qTVCharCYc+qwqNrMuwaJtFogY4X4tECG10nd9pVsIK2WoB91epenJflOytxpAZA8n1dHd60gl82Sp66MZ+5ljMX26KSpeT1vyBZrRWLCzp2IHzsQDRK+o2otrw4aMhgtP+PaJUthsz23IOfEUan2fgDFacLbuuNZqcr0OEOn1hKvTWxG4LC9+Lo36qVQ3rY63f6jarKYdl5fMYbs23dcQHosLV+/FKvKuGywhEs9OLiMlf7C58Okdf18dDALPQbyFcOaQRsQOIYBLox96OTsTsbpEInEzqJsM8vWQ7rOCNOwo25H50UJKzfWucp7r3EYW9GasdhYdBVSs9PNt1ta9/W0pz3EyOLy85V7B/4Y7vJxZA0pzrxU+mcz25k1fxStLWouiSGWG7VVvuaHOV3KQq5galf6CDhNlz/hA34u6VYtaLfeOWOYh4wtxqO8/PWbafqbas27+rdR8iFGxuYz/pdznXRysamHMqB+C/FMatKqTn0jXL8nK06cL2w/QHgMRYaqMetWavWnbaARmC0xVaJDZytkHHp5TJ0gPkXd2izeCKV/wlMNjQ7v34MGCzfmWouKXnVrLk92HVOV/wg2hMYnL7fVXkTHMDeeQBl3VgFNrqNED4x/I7hogGFrp5OiAnw1mhvj+hAqOgA1TYNgdev/aHdn1qtt7bKTrjY370RKsgfD9RnIHvzfSFbyr0o/Z2jpTEWMXVYhFNGngSLQm02vC5R7U4q50AWwbFx8tDmEOLY4uKd3pp+gXtVnYJbsFreGVDjX41q+GBM3y+XWhiHVujzht6H+BFcMqU9uBSfNpTIYT2Bd0CchscPvkmxBvr9JbzUaNcHTMf47uIfsiyFO+v5DvTf2j+iPe/JTVPJQpr74/O+BQJYqZpXd0TqjY8UvxWp4hGRKr5LpJLMAT/B+GGhmtwZokMfw2snkTL2rePzwXHJaViKW/E4uz8ep4R09kUBwcQfKtz41Dz+JSxOplmCKaFZGCWEJAT3pQZRijKSYkwyFkf0GUjt3qI580VzO0j5I4om/z701rVF9sCaGfjt7uoB3JMpwxQznNA4JUmWRt+ggO7L/V9/rPPLl+S9RZ11x5coffbjy29/C8QyMpDDsyP29v8fsXDqDzruy+wnp88PqjoAe97gzV89b/4GA7Eg3qRPeEmr4C0Ye7GlFythiBaB+Fz/8wb7CAyqvpSKPh3cEZwn3TOOXHxjfIuc8WPC++kc1GJlZ8eNfCYLH7/RR+bhuFPHZGgT8WmbYF2bSOL+TP3EncHlUGVz/V1tRKuFewO+/V5/KURjv1B5X39sea3tP2lO35oeDn3540APiHfnIs+B1z0b/l2wFj8Q1sT148PQoq/d28MznXieBevZ+Fsi9/Vr95/E1/8DUEsHCIuGp+zwBgAA5hwAAFBLAQIUABQACAAIAHSn3kDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAdKfeQIuGp+zwBgAA5hwAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACHBwAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br /><br /> | ||
| + | |||
| + | =====Satz X.3:===== | ||
| + | Die Verkettung dreier Geradenspiegelungen, deren Achsen nicht alle parallel zueinander oder kopunktal sind, ist stets eine Schubspiegelung.<br /> | ||
Beweis:<br /><br /> | Beweis:<br /><br /> | ||
Aktuelle Version vom 6. Juli 2012, 13:30 Uhr
Inhaltsverzeichnis |
Verkettung von drei Geradenspiegelungen
Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei Geradenspiegelungen? (gerne auch als Bild).
Satz X.1:
- Die Verkettung von drei Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
an zueinander parallelen Geraden a, b und c ist eine Geradenspiegelung an einer Geraden d mitund
.
Beweis:
muss die gerade d nicht noch genauer beschrieben werden? es gibt doch zwei zu c parallele geraden die den gleichen abstand (wie die gerade a und b) haben--Studentin 23:08, 1. Jul. 2012 (CEST)
mmh, gut mitgedacht - was meinen die Anderen?--Schnirch 15:29, 2. Jul. 2012 (CEST)
seh ich genauso, das problem ergibt sich unten bei den Winkeln ebenso, oder nicht? Nelson 14:23, 6. Jul. 2012 (CEST) wobei die Winkel unten gerichtet sind, also doch nicht... Nelson 14:30, 6. Jul. 2012 (CEST)
Satz X.2:
- Die Verkettung von drei Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
, an drei Geraden a, b und c die sich in einem Punkt S schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse d, die durch den Punkt S verläuft mit 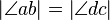 .
.
Beweis:
Definition X.1 (Schub- oder Gleitspiegelung)
Eine Schub- oder Gleitspiegelung ist eine Abbildung, die bei der Verkettung dreier Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
entsteht, wenn die zwei Geraden a und b parallel zueinander und die dritte Gerade c senkrecht dazu steht.
Experimentieren Sie mit der nachfolgenden GeoGebra-Applikation. Welche Eigenschaften der Schubspiegelung entdecken Sie?
Satz X.3:
Die Verkettung dreier Geradenspiegelungen, deren Achsen nicht alle parallel zueinander oder kopunktal sind, ist stets eine Schubspiegelung.
Beweis:

