Verkettung von drei Geradenspiegelungen SoSe 12
Inhaltsverzeichnis |
Verkettung von drei Geradenspiegelungen
Aufgabe: Welche prinzipiellen Möglichkeiten bezüglich der Lage der Achsen gibt es bei der Verkettung von drei Geradenspiegelungen? (gerne auch als Bild).
Satz X.1:
- Die Verkettung von drei Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
an zueinander parallelen Geraden a, b und c ist eine Geradenspiegelung an einer Geraden d mitund
.
Beweis:
muss die gerade d nicht noch genauer beschrieben werden? es gibt doch zwei zu c parallele geraden die den gleichen abstand (wie die gerade a und b) haben--Studentin 23:08, 1. Jul. 2012 (CEST)
mmh, gut mitgedacht - was meinen die Anderen?--Schnirch 15:29, 2. Jul. 2012 (CEST)
seh ich genauso, das problem ergibt sich unten bei den Winkeln ebenso, oder nicht? Nelson 14:23, 6. Jul. 2012 (CEST) wobei die Winkel unten gerichtet sind, also doch nicht... Nelson 14:30, 6. Jul. 2012 (CEST)
Satz X.2:
- Die Verkettung von drei Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
, an drei Geraden a, b und c die sich in einem Punkt S schneiden (kopunktal), ist eine Geradenspiegelung an einer Achse d, die durch den Punkt S verläuft mit 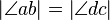 .
.
Beweis:
Definition X.1 (Schub- oder Gleitspiegelung)
Eine Schub- oder Gleitspiegelung ist eine Abbildung, die bei der Verkettung dreier Geradenspiegelungen Fehler beim Parsen(Unbekannte Funktion „\cir“): S_{a}\cir S_{b} \cir S_{c}
entsteht, wenn die zwei Geraden a und b parallel zueinander und die dritte Gerade c senkrecht dazu steht.
Experimentieren Sie mit der nachfolgenden GeoGebra-Applikation. Welche Eigenschaften der Schubspiegelung entdecken Sie?
Satz X.3:
Die Verkettung dreier Geradenspiegelungen, deren Achsen nicht alle parallel zueinander oder kopunktal sind, ist stets eine Schubspiegelung.
Beweis:

