Lösung von Aufgabe 5.3 S (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
 
(11 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 2: Zeile 2:
 
Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math> <br />
 
Wenn <math> C \in \ AB^{+} </math> und <math>\left| AB \right| < \left| AC \right| </math> dann gilt <math>\operatorname Zw (A, B, C) </math> <br />
 
<br />
 
<br />
 +
 +
Hier mal meine Lösung. Habe mein Beweis abfotografiert und hoffe man kann ihn erkennen .....
 +
 +
[[Datei:Beispiel1.jpg]]
 +
  
 
ich habe Schwierigkeiten das Plus beim B zu interpretieren. Ist Zw. (ABC) eine fertige Aussage?--[[Benutzer:KeinKurpfälzer|KeinKurpfälzer]] 17:09, 21. Mai 2012 (CEST)<br /><br />
 
ich habe Schwierigkeiten das Plus beim B zu interpretieren. Ist Zw. (ABC) eine fertige Aussage?--[[Benutzer:KeinKurpfälzer|KeinKurpfälzer]] 17:09, 21. Mai 2012 (CEST)<br /><br />
Zeile 45: Zeile 50:
 
Zw (B,A,C) kann nicht gelten, da nach Voraussetzung <math> C \in \ AB^{+} </math> gelten muss. Bei Zw (B,A,C) liegt C aber auf<math> \ AB^{-} </math>.. Widerspruch zur Voraussetzung.--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 17:12, 19. Jun. 2012 (CEST)
 
Zw (B,A,C) kann nicht gelten, da nach Voraussetzung <math> C \in \ AB^{+} </math> gelten muss. Bei Zw (B,A,C) liegt C aber auf<math> \ AB^{-} </math>.. Widerspruch zur Voraussetzung.--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 17:12, 19. Jun. 2012 (CEST)
  
−
ich habe den beweis, den wir im tutorium geführt haben nicht so recht verstanden! allgemein hab ich ein problem mit dem "einsetzen" bei beweisen!hier der link zu meinem foto, hab es aus versehen irgendwo anders hochgeladen und kann des nicht mehr löschen und es deshalb hier nicht mir reinstellen!
+
 
−
also meine probleme stehen auf dem blatt:
+
 
−
http://wikis.zum.de/geowiki/images/1/16/Zimma_016.jpg
+
 
 +
===Verständnisprobleme beim Beweis von 5.3 im Tutorium, bitte um Hilfe===
 +
[[Bild:Zimma_016.jpg|400px]]
 +
 
 +
ich habe den beweis, den wir im tutorium geführt haben nicht so recht verstanden! allgemein hab ich ein problem mit dem "einsetzen" bei beweisen!
 +
also meine probleme stehen auf dem blatt.
 +
 
 
--[[Benutzer:Gauglera|Gauglera]] 22:22, 7. Jul. 2012 (CEST)
 
--[[Benutzer:Gauglera|Gauglera]] 22:22, 7. Jul. 2012 (CEST)
 +
 +
====Bemerkungen von M.G.====
 +
Ich glaube nicht dass Sie ein Problem mit dem Einsetzen von Termen in Gleichungen bei Beweisen haben. Im Gegenteil, Sie haben ein sicheres Gespür gehabt, dass mit dem Beweis aus dem Tutorium etwas nicht stimmt. Hier der Inhalt meiner Mail an Sie, damit alle davon profitieren.
 +
====Die Mail====
 +
Sehr geehrte Frau ... ,<br />
 +
Sie haben Recht, der Beweis aus dem Tutorium ist  nicht korrekt.
 +
 +
Wir gehen davon aus. dass alle betrachteten Punkte paarweise verschieden
 +
sind.
 +
 +
Unser Punkt <math>C </math>liegt nach Voraussetzung auf der Halbgeraden
 +
<math>AB^+</math>. Damit liegt er (1) entweder auf der offenen Strecke
 +
<math>\overline{AB}</math> oder (2) auf der Verlängerung dieser Strecke über
 +
<math>B</math> hinaus. Wir schreiben (1) und (2) formal als Gleichung:
 +
 +
(1)  <math>|AC|+|CB|=|AB|</math>
 +
 +
(2)  <math>|AB|+|BC|=|AC|</math>.
 +
 +
Wie bereits gesagt, genau eine der beiden Gleichungen muss gelten.
 +
(<math>C</math> gehört ja zu <math>AB^+</math>.)
 +
 +
Wir sollen zeigen, dass der Punkt<math>B</math> zwischen den Punkten
 +
<math>A</math> und <math>C</math> liegt. Das wäre entsprechend der
 +
Definition der Zwischenrelation äquivalent zu der Aussage, dass Gleichung
 +
(2) gilt.
 +
 +
Jetzt kommt unser Widerspruchsbeweis:
 +
 +
Wir nehmen an, dass (1) gilt.  Völlig zurecht haben Sie erkannt, dass dieses
 +
unsere Annahme sein muss und der Zusatz "und nicht
 +
<math>\operatorname{Zw}(A,C,B)</math>" keinen Sinn macht. ( Wir wissen doch
 +
schon lange, dass von drei paarweise verschiedenen Punkten genau einer
 +
zwischen den beiden anderen liegen muss.)
 +
 +
Weiter mit dem Beweis:
 +
 +
Wir nehmen also an, dass die Gleichung (1) gilt. Die Abstände <math> |AC|,
 +
|CB|, |AB|</math> sind positive reelle Zahlen. Für alle positiven reellen
 +
Zahlen gilt: Die Summe zweier derartiger Zahlen ist immer größer als die
 +
einzelnen Summanden.  Übertragen auf unsere Gleichung bedeutet das, dass der
 +
Abstand <math>|AB|</math> größer als der Abstand <math>|AC|</math> ist. Das
 +
ist aber ein Widerspruch zur Voraussetzung <math>|AB|<|AC|</math>.
 +
 +
Im Beweis aus dem Tutorium wird an keiner Stelle die Voraussetzung
 +
<math>|AB|<|AC|</math> benutzt.  Werden beim Beweis eines Satzes nicht alle
 +
Voraussetzungen des Satzes verwendet, dann ist das immer ein Hinweis darauf,
 +
dass etwas nicht stimmt: entweder der Beweis ist falsch oder der Satz nicht
 +
korrekt formuliert. Letzteres ist bei unserer Aufgabe sicherlich nicht der
 +
Fall.
 +
 +
Viele Grüße<br />
 +
Michael Gieding
 +
 +
 +
--[[Benutzer:*m.g.*|*m.g.*]] 08:58, 8. Jul. 2012 (CEST)

Aktuelle Version vom 11. Juli 2012, 19:29 Uhr

Zeigen Sie, dass für drei paarweise verschiedene Punkte \ A, B und \ C gilt:
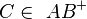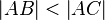Wenn C \in \ AB^{+} und \left| AB \right| < \left| AC \right| dann gilt \operatorname Zw (A, B, C)

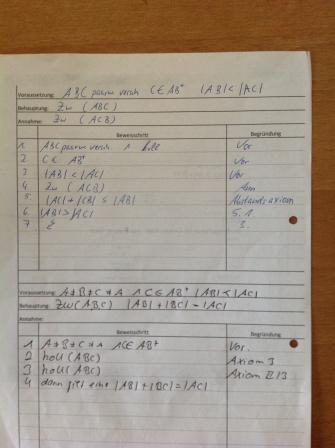
Hier mal meine Lösung. Habe mein Beweis abfotografiert und hoffe man kann ihn erkennen .....

Beispiel1.jpg


ich habe Schwierigkeiten das Plus beim B zu interpretieren. Ist Zw. (ABC) eine fertige Aussage?--KeinKurpfälzer 17:09, 21. Mai 2012 (CEST)

Gut, dass Sie fragen. 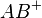AB^{+} ist die Halbgerade, die bei A beginnt und in Richtung B verläuft. Werden wir am Donnerstag behandeln. Und Ihre zweite Frage: Ja, \operatorname Zw (A, B, C) ist eine fertige Aussage. In Worten: B liegt zwischen A und C.--Buchner 10:28, 22. Mai 2012 (CEST)

5.3.JPG

--H2O 18:58, 21. Mai 2012 (CEST)


Was mache ich Warum darf ich das?
C Element ABplus Voraussetzung
koll(A,B,C) (1)
AB| + |BC| = |AC|; |BC| + |CA| = |BA|; |BA| + |AC| = |BC Zwischenrelation, (2)
Zw(A,B,C) v Zw(A,C,B) v Zw(B,A,C) Zwischenrelation, (3)


Nun ist gezeigt, dass eine der Zwischenrelationen gilt (Existenz).
Frage: Habe ich zwei Möglichkeiten?
1.:
Ich zeige, dass Zw(B,A,C) (1. Annahme) und dass Zw(A,C,B) (2. Annahme) nicht gilt.
2.:
Ich zeige, dass zwei Zwischenrelationen nicht gelten.
Ich bin der Meinung, dass die erste Möglichkeit als einzige möglich sein müsste, weil wir ja konkret beweise müssen, dass B zwischen A und C liegt.
Oder muss ich beide Annahmen zum Widerspruch führen?
--RitterSport 15:01, 30. Mai 2012 (CEST)

Inhaltsverzeichnis

Anmerkungen von Buchner

Ich stimme Ihnen absolut zu, RitterSport. Sie müssen zeigen, dass weder Zw(B,A,C) noch Zw(A,C,B) gilt.Gemeinsam mit dem Wissen, dass auf jeden Fall eine der drei Gleichungen, d.h. eine der Zwischenrealtionen, gelten muss, haben Sie dann die Aufgabe gelöst. H2O hat schon durch Widerspruchsbeweis Zw (A,C,B) ausgeschlossen- der Beweis ist richtig. Um Zw (B,A,C) auszuschließen brauchen Sie eigentlich keinen großen Beweis- ein paar erklärende Worte genügen. Viel Erfolg!--Buchner 15:57, 31. Mai 2012 (CEST)

Wieso muss ich zeigen, dass nur eine gilt, und dann, dass Zw(A,B,C) gilt? Ist es nicht ausgeschlossen, dass mehr gelten, wenn Zw(A,C,B) und Zw(B,A,C) nicht gelten?--RitterSport 11:34, 1. Jun. 2012 (CEST)
Also wenn man zeigt, dass Zw(B,A,C) und Zw(B,C,A) nicht gelten und man weiß, dass eine der drei Zwischenrelationen gilt, dann hat man gezeigt, dass Zw(A,B,C) gilt.--Tutor Andreas 12:18, 19. Jun. 2012 (CEST)

Zw (B,A,C) kann nicht gelten, da nach Voraussetzung 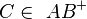C \in \ AB^{+} gelten muss. Bei Zw (B,A,C) liegt C aber auf 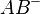\ AB^{-} .. Widerspruch zur Voraussetzung.--Tchu Tcha Tcha 17:12, 19. Jun. 2012 (CEST)



Verständnisprobleme beim Beweis von 5.3 im Tutorium, bitte um Hilfe

Zimma 016.jpg

ich habe den beweis, den wir im tutorium geführt haben nicht so recht verstanden! allgemein hab ich ein problem mit dem "einsetzen" bei beweisen! also meine probleme stehen auf dem blatt.

--Gauglera 22:22, 7. Jul. 2012 (CEST)

Bemerkungen von M.G.

Ich glaube nicht dass Sie ein Problem mit dem Einsetzen von Termen in Gleichungen bei Beweisen haben. Im Gegenteil, Sie haben ein sicheres Gespür gehabt, dass mit dem Beweis aus dem Tutorium etwas nicht stimmt. Hier der Inhalt meiner Mail an Sie, damit alle davon profitieren.

Die Mail

Sehr geehrte Frau ... ,
Sie haben Recht, der Beweis aus dem Tutorium ist nicht korrekt.

Wir gehen davon aus. dass alle betrachteten Punkte paarweise verschieden sind.

Unser Punkt C liegt nach Voraussetzung auf der Halbgeraden AB^+. Damit liegt er (1) entweder auf der offenen Strecke \overline{AB} oder (2) auf der Verlängerung dieser Strecke über B hinaus. Wir schreiben (1) und (2) formal als Gleichung:

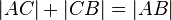
(1) |AC|+|CB|=|AB|

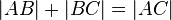(2) |AB|+|BC|=|AC|.

Wie bereits gesagt, genau eine der beiden Gleichungen muss gelten. (C gehört ja zu AB^+.)

Wir sollen zeigen, dass der PunktB zwischen den Punkten A und C liegt. Das wäre entsprechend der Definition der Zwischenrelation äquivalent zu der Aussage, dass Gleichung (2) gilt.

Jetzt kommt unser Widerspruchsbeweis:

Wir nehmen an, dass (1) gilt. Völlig zurecht haben Sie erkannt, dass dieses unsere Annahme sein muss und der Zusatz "und nicht 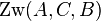\operatorname{Zw}(A,C,B)" keinen Sinn macht. ( Wir wissen doch schon lange, dass von drei paarweise verschiedenen Punkten genau einer zwischen den beiden anderen liegen muss.)

Weiter mit dem Beweis:

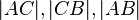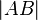Wir nehmen also an, dass die Gleichung (1) gilt. Die Abstände |AC|, |CB|, |AB| sind positive reelle Zahlen. Für alle positiven reellen Zahlen gilt: Die Summe zweier derartiger Zahlen ist immer größer als die einzelnen Summanden. Übertragen auf unsere Gleichung bedeutet das, dass der Abstand |AB| größer als der Abstand 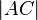|AC| ist. Das ist aber ein Widerspruch zur Voraussetzung |AB|<|AC|.

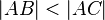Im Beweis aus dem Tutorium wird an keiner Stelle die Voraussetzung 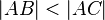|AB|<|AC| benutzt. Werden beim Beweis eines Satzes nicht alle Voraussetzungen des Satzes verwendet, dann ist das immer ein Hinweis darauf, dass etwas nicht stimmt: entweder der Beweis ist falsch oder der Satz nicht korrekt formuliert. Letzteres ist bei unserer Aufgabe sicherlich nicht der Fall.

Viele Grüße
Michael Gieding


--*m.g.* 08:58, 8. Jul. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_5.3_S_(SoSe_12)&oldid=16501“