Lösung von Testaufgabe 2.6 SS12: Unterschied zwischen den Versionen
Mahe84 (Diskussion | Beiträge) |
|||
| (8 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Ein Viereck | + | Ein Viereck dessen Diagonalen senkrecht aufeinander stehen und eine davon halbiert wird, ist ein Drachenviereck. <br /> |
Vor.: Viereck ABCD, AC senkrecht auf BD und DM = MB<br /> | Vor.: Viereck ABCD, AC senkrecht auf BD und DM = MB<br /> | ||
| Zeile 6: | Zeile 6: | ||
1. AC senkrecht auf BD / Vor.<br /> | 1. AC senkrecht auf BD / Vor.<br /> | ||
| − | 2. < DMC | + | 2. < DMC = <BMC, = <AMB = <AMD / def. senkrecht <br /> |
3. DM = MB / Vor.<br /> | 3. DM = MB / Vor.<br /> | ||
4. CM = CM / trivial<br /> | 4. CM = CM / trivial<br /> | ||
| Zeile 16: | Zeile 16: | ||
10. AD + BC = AB + DC / 8. 9.<br /> | 10. AD + BC = AB + DC / 8. 9.<br /> | ||
11. Jeder Drachen ist ein Tangentenviereck q.e.d / 10.<br /> | 11. Jeder Drachen ist ein Tangentenviereck q.e.d / 10.<br /> | ||
| + | --[[Benutzer:Mahe84|Mahe84]] 19:00, 14. Jul. 2012 (CEST) | ||
| + | <br /> | ||
| + | |||
| + | |||
| + | Lösungsversuch Nummero6/Tchu Tcha Tcha:<br /> | ||
| + | |||
| + | '''Ein Viereck mit 2 Paar aneinanderliegenden , gleich langen Seiten nennt man Drachen.'''<br /> | ||
| + | |||
| + | '''Voraussetzung:''' oBdA <math>\left| a \right| =\left| d \right| \wedge b \left| b \right| =\left| c \right|</math><br /> | ||
| + | '''Behauptung:''' <math>\left| a \right| +\left| c \right| = \left| b \right| +\left| d \right|</math><br /> | ||
| + | '''Annahme:''' <math>\left| a \right| +\left| c \right| \neq \left| b \right| +\left| d \right|</math><br /> | ||
| + | [[Datei:Test 2.6.png]] | ||
| + | <br />--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 19:46, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | Es sei ABCD ein Viereck. Wenn jeweils zwei benachbarte Seiten kongruent zueinander sind, dann ist dieses Viereck ein Drachen. | ||
| + | |||
| + | Vor.: a = d und b = c | ||
| + | Beh.: a + c = b + d | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable " | ||
| + | ! Schritt | ||
| + | ! | ||
| + | ! Begründung | ||
| + | |- | ||
| + | | 1 | ||
| + | | a=d und b=c | ||
| + | | Vor., Def. Drachen | ||
| + | |- | ||
| + | | 2 | ||
| + | | AC=AC | ||
| + | | trivial | ||
| + | |- | ||
| + | | 3 | ||
| + | | ABC=CDA | ||
| + | | (1),(2),SSS | ||
| + | |- | ||
| + | | 4 | ||
| + | | a+b=c+d | ||
| + | | (3),Rechnen in R | ||
| + | |- | ||
| + | | 5 | ||
| + | | a+c=b+d | ||
| + | | (4),(1),Rechnen in R (einsetzen)q.e.d. | ||
| + | |} --[[Benutzer:LuLu7410|LuLu7410]] 21:05, 14. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
| + | |||
| + | Definition: Ein Drache ist ein Viereck mit zwei Paaren gleichlanger benachbarter Seiten. | ||
| + | |||
| + | VSS: Drachenviereck, AD = CD, AB = BC (AD, CD, AB, BC sind natürlich Strecken) | ||
| + | |||
| + | Beh: Tangentenviereck AD + AB = CD + BC | ||
| + | |||
| + | Ann: AD + BC "ungleich" CD + AB | ||
| + | |||
| + | (1) AD = CD und BC = AB /Def. Drachenviereck | ||
| + | |||
| + | (2) AD + BC "ungleich" CD + AB / Annahme | ||
| + | |||
| + | (3) CD + BC = CD + BC / (1), (2), Rechnen in R | ||
| + | |||
| + | Widerspruch zur Annahme, Behauptung gilt | ||
| + | --[[Benutzer:Gauglera|Gauglera]] 18:51, 15. Jul. 2012 (CEST) | ||
Aktuelle Version vom 15. Juli 2012, 17:52 Uhr
Ein Viereck dessen Diagonalen senkrecht aufeinander stehen und eine davon halbiert wird, ist ein Drachenviereck.
Vor.: Viereck ABCD, AC senkrecht auf BD und DM = MB
Beh.: AD + BC = AB + DC
1. AC senkrecht auf BD / Vor.
2. < DMC = <BMC, = <AMB = <AMD / def. senkrecht
3. DM = MB / Vor.
4. CM = CM / trivial
5. Dreieck DMC = Dreieck BMC / 2. 3. 4. SWS
6. AM = AM / trivial
7. Dreieck AMD = Dreieck AMB / 2. 3. 6. SWS
8. DM = AB / 7.
9. DC = BC / 5.
10. AD + BC = AB + DC / 8. 9.
11. Jeder Drachen ist ein Tangentenviereck q.e.d / 10.
--Mahe84 19:00, 14. Jul. 2012 (CEST)
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Ein Viereck mit 2 Paar aneinanderliegenden , gleich langen Seiten nennt man Drachen.
Voraussetzung: oBdA 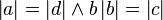
Behauptung: 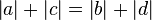
Annahme: 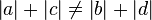
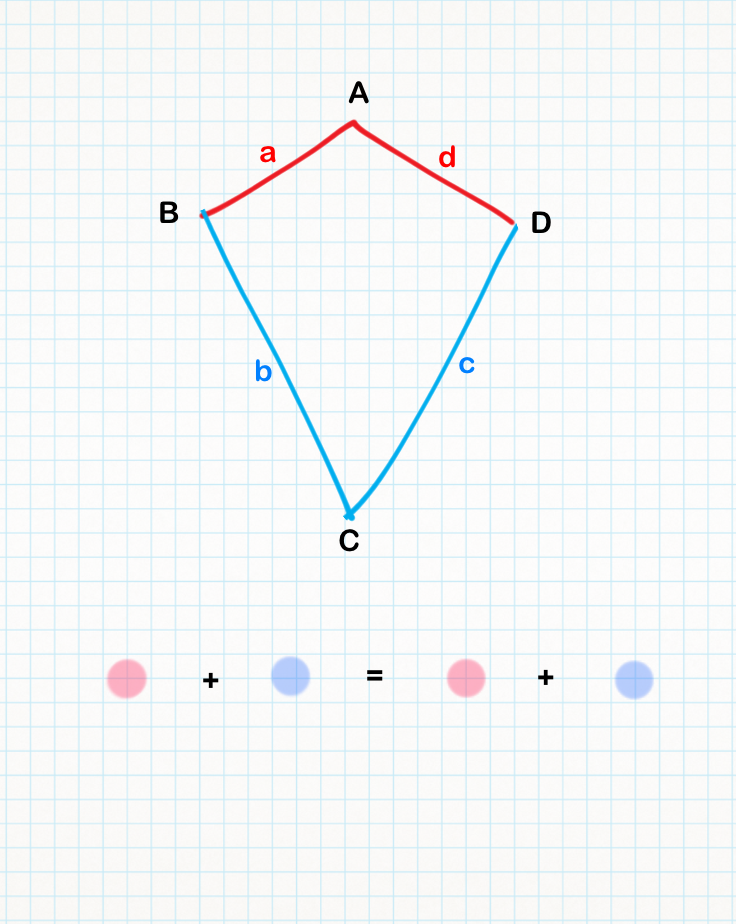
--Tchu Tcha Tcha 19:46, 14. Jul. 2012 (CEST)
Es sei ABCD ein Viereck. Wenn jeweils zwei benachbarte Seiten kongruent zueinander sind, dann ist dieses Viereck ein Drachen.
Vor.: a = d und b = c Beh.: a + c = b + d
| Schritt | Begründung | |
|---|---|---|
| 1 | a=d und b=c | Vor., Def. Drachen |
| 2 | AC=AC | trivial |
| 3 | ABC=CDA | (1),(2),SSS |
| 4 | a+b=c+d | (3),Rechnen in R |
| 5 | a+c=b+d | (4),(1),Rechnen in R (einsetzen)q.e.d. |
Definition: Ein Drache ist ein Viereck mit zwei Paaren gleichlanger benachbarter Seiten.
VSS: Drachenviereck, AD = CD, AB = BC (AD, CD, AB, BC sind natürlich Strecken)
Beh: Tangentenviereck AD + AB = CD + BC
Ann: AD + BC "ungleich" CD + AB
(1) AD = CD und BC = AB /Def. Drachenviereck
(2) AD + BC "ungleich" CD + AB / Annahme
(3) CD + BC = CD + BC / (1), (2), Rechnen in R
Widerspruch zur Annahme, Behauptung gilt --Gauglera 18:51, 15. Jul. 2012 (CEST)

