Sehnenviereck SS 12: Unterschied zwischen den Versionen
Oz44oz (Diskussion | Beiträge) (→Beweis vom Satz 2) |
Oz44oz (Diskussion | Beiträge) (→Funktionale Betrachtung) |
||
| (49 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
| − | === | + | === Kreissehne === |
| + | 1. Es sei <math>\ k</math> ein Kreis. Eine Sehne des Kreises ist jede Strecke, deren Anfangs- und Endpunkte Element des Kreises <math>\ k</math> sind. | ||
| + | 2. .......... | ||
| + | === Durchmesser=== | ||
| − | + | 1. Es sei <math>\ k</math> ein Kreis mit dem Mittelpunkt <math>\ M </math>. Ferner seien <math>\ A</math> und <math>\ B </math> zwei Punkte des Kreises <math>\ k</math>. Ein Durchmesser ist die Strecke <math>\overline {AB}</math>, für die gilt <math> \operatorname{Zw} \left( A, M, B\right)\wedge A,B\in \ k</math>. | |
| + | === Radius === | ||
| + | |||
| + | 1. Es sei <math>\ k</math> ein Kreis mit dem Mittelpunkt <math>\ M </math>. Jede Strecke, die den Anfangspunkt in <math>\ M </math> und den Endpunkt in einem beliebigen Punkt des Kreises <math>\ k</math> hat, nennt man Radius. | ||
| + | |||
| + | === Erarbeitung des Begriffs Sehnenviereck === | ||
| + | |||
| + | [[Datei:Sehnenvierecke.pdf]] | ||
| + | |||
| + | === Sehnenviereck === | ||
| + | |||
| + | Ein Viereck, dessen Seiten Sehnen ein und desselben Kreises <math>k</math> sind, heißt Sehnenviereck. | ||
== Sätze == | == Sätze == | ||
| Zeile 17: | Zeile 31: | ||
===Satzfindung=== | ===Satzfindung=== | ||
| − | === | + | ==== sehr speziell: Quadrate ==== |
| + | Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.<br /><br /> | ||
| + | [[Bild:Quadrat_als_Sehnenviereck.png]] | ||
| + | ==== weniger speziell, aber immer noch ziemlich speziell: Rechtecke ==== | ||
| + | Jedes Rechteck ist ein Sehnenviereck. | ||
| + | <ggb_applet width="419" height="444" version="3.2" ggbBase64="UEsDBBQACAAIAEKv9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VrLcts2FF03X8HhXjQeJEjMSMlIdheZSetMnWbRTYYiIQk1RaokZEv+qyb5jn5TLwBST0s2/Yhjz3ggXoDAxTn3XDyk7rvFNHOuRFnJIu+52EOuI/KkSGU+7rlzNepE7ru3b7pjUYzFsIydUVFOY9VzqUdcbZ/Lt29+6VaT4tqJM9PksxTXPXcUZ5VwnWpWijitJkKoLXs8X8hMxuXyfPi3SFS1rrCdvM9ncxhFlXOwJdP0g6yaxxMz4CyT6kxeyVSUTlYkPZcF4Dp8+ixKJZM467k+shbSc8lOJZiorp0UpbwpcqWbrzsfgcVxKnkj4E2kbd0TM9GumCeZTGWc68kYP6CR41zLVE1gQMyhSyHHE6VH57a3pCjK9GJZKTF1Fn+Jsui5Hcy8wA8JxZwGiIUsCF1naes493yMQ59w5gc0wBhABI/BFco9gpgfhhjmSjAK4J2DVWZocXUhlAIqKydeiDXI41KmWw/vq0GRrU2zQubqNJ6peWnigNamC7XUowFwpZ5kPx9norYRoGkiksthsbgwwGFqu/60nJlXjEPD8WmRFaVTakrA/3FdDm1p2mhPV62QaYNMi7oP3emqHnNiWphyaEvTKpO5da2eOW5mjVEzjKwcbYDOdfiuJp/FQwHh4DrzXKoPzQOEzWU9VWxf+H0+HYJuNgNn1Sd+qj67Jzsh170UZS4yG1g5cDsv5pVzpQPYjmUcSUUip/BoK2pIYk3Xn+CAtaZiXIrGcas6C5ipRZvBu2PunjROaB8q8DVRkD5gPkrPRatbgbJ67tQbe66TxkpbtXwyMRWgLWViwoTUCpvf3FUiKUxOaNRf169Rhupb48NEUpzNJjFYvHoCWbyEDLE5JdPf+WhUCeUsQIug2SWEON2o/a1It2GIc4DTzBFkPNPda8JmQqR1zlR1lDszGNBoZoMNA2KlB2O6LYzWofrDjX3ZtLH60tnEjEtr8i1gd0A3+IL3wduOvA1vngK+ZwOI1wChtvgkxXQa56mTx1MY51SWSSYMKFKvJE6MdIQ5MbZoWSDmqqlKbHd1J3twQ5TLZIVl4m4nGDUBHeeiqkwWVJv57nA434MQ9HA67uUcLFQivwLXirJynAWqmVqiBv7GsgDUOsa0xLXpBm9wA8yXcuH0m/b9plVfL73M41t/DOy0HqLvQ89GFP1A7ykaz/7JrfeVzY4QSIkcyeQ46R+NKLY5T/ao7h+neltZ/QclJUzs0mbKhycm4hspkOhHCI94lDKKCUJRGFEW4sAmqsDDlPtgCaA+IBF7jCw/QFjuENS3olz0Yenc4yo+zpWO8hUV8QNV2TpPPkKWa7hRnedwnef2YW6h4x21yClsjhOpjnPxPlew0wAI9hRjCImh0OptprjByqCNggYPUhDzDeC6GNqitXyIBZji+xHCPcYoi0LOMcGMguiePvzPS9gWjYs8zm4RwqDBfRfuYQsRDF+VCDp4Z7XfJ+G5VXCUkv4hStIWlKSvm5Jb1oUXzkzDw5nptE1mOv2xmal97kFexFAABh+q/RD7+DHJ5w5U08OonrVB9eyl8n2HUAsbDu+H+qEdzy7sAXkM7B+LbAn55fbMMrCgn0JBa5y3kIcjfyaSS1znoS/Yth+aD/BGYj7AHjq1Z5pjJFk3GhpWPT/fUQYH1JAa4L30hNso5fApuBJj/bTeAn55ofk8ehsYepSENAx4RHxKWGC3GTT0WBBxwlFEw9BH/hOlXhNjmT4MrJICHCD2b5EuhZjp67vz/FMZ55W++rVtNm6n7knN8NVR0/E9EkachRTp/yDEW+uijz19dYt8HrIo4E+1Kr4ANcmrowZ7GCNCKCI+IwEOWPBrp8netyupwzygEJ4jjCKCOX69dKWvjq5dIaFgS0kd7nEeIkRCRDkKafBUZ99nIWd7dTffgOys7Wd2te7btXqwt6j/9+/xpdpc0694gtb6ffBnXuPreyEmNIp4hGjkM34X08cuzjHaPzscX5w3NlzY3pwf2G+1kVhcJusNVdQYs6y4/kOMMrEwMO/w1o6U3Q3XHilfW5Hy9aclpT48YP4KSKmVcnpQKd9akfJtlxTsQbIJOZyoWMh9SEHs5Wjh9eHk9q+Zfi5earGcHRTL91a8fL+Tl+jlchirebn9mvBH8nKy+V2q+clB/ZuLt/8DUEsHCFxRBbNRBgAApSEAAFBLAQIUABQACAAIAEKv9TxcUQWzUQYAAKUhAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAiwYAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | ==== noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze ==== | ||
| + | Jedes gleichschenklige Trapez ist ein Sehnenviereck. | ||
| − | ==== | + | <ggb_applet width="419" height="411" version="3.2" ggbBase64="UEsDBBQACAAIAJGx9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s1VrbbtvGFn1uv4LgQ9GiNT1XcohaKWT7JUDcFHVOcNALCoocSVNTpEqOHMkH56OK/sf5prNnhpQlSpYtxU7sPITi3Getvfbs2ebJD/NJ7l3LqlZl0fNxgHxPFmmZqWLU82d6eCT8H159eTKS5UgOqsQbltUk0T2fBsQ35TP16ssvTupx+cFLctvkvZIfev4wyWvpe/W0kklWj6XUa+XJbK5ylVSLt4M/Zarr2wo3yOtiOoNZdDWDsnSSvVF1+3psJ5zmSp+ra5XJysvLtOeHHJYOv97LSqs0yXs+Q66E9HzSqYQiamrHZaVuykKb5reDD6HE82p1I6EnMmUnx3ajJ3KW5ipTSWE2Y9cBjTzvg8r0GCbEMQwp1WiszeyxGy0tyyq7XNRaTrz5L7Iqe/4RDgPOIkJxTDkKo5BHvrdwdXEcMIwjRuKQccoxBhBhxbAUGgcEhSyKMOyVYMShz51Vdmp5fSm1BiprL5nLW5BHlcrWXl7Xp2V+WzQtVaHPkqmeVdYOaFN0qRdmNgCuMpvsF6NcNmUEaBrL9GpQzi8tcJi6od8tpraLXdBgdFbmZeVVhhJY/6h5DtzTtjErXbZCtg2yLZoxzKDLehwT28I+B+5pW+WqcEtrdo7bXWPUTqNqzxTA4MZ8l5vPk4EEc/C9WaH0m/YFzOaq2Sp2HX6cTQagm1XDWY6JH2vMk+OOyZ1cyaqQuTOsAridlbPauzYG7OayC8lkqibw6ipwszpD179gAa40k6NKtgt3qnOA2Vq0aryd4pPjdhFmDTWsNdXgPmA/2uzFqFuDsnr+JBgFvpcl2pQa+eRyIkFb2tqENaklNhf+0pGU1ie06m/qb1GG6q32YS0pyafjBEqCZgN5sgAPsbolO97b4bCW2puDFkGzCzBxulJ7UWbrMCQFwGn3CDKemuENYVMps8Zn6sbKvSlMaDWzwoYFsTaThaYtzHZEzY8b19m2cfoy3sTOSxvyHWD3QHf6B94Eb93yVlbzGPA9GUBxAxDaF5+0nEySIvOKZALznKkqzaUFRZmTxEuQsTAvwQ4tB8RMt1WpG64ZZANusHKVLrFM/XUHo8eg40LWtfWCetXf3W3ODyAEHU7HgxYHB5UsrmFpZVV73hw1TC1QC39bMgfUjmzRAjdFN3iFG2C+UnOv37bvt6365ugNg3jtXwjltJmiz2BkK4o+NzFFu7K/Crf62nlHMKRUDVW6m/SfrCjWOU83qO7vpnpdWf2DnBIm7mizz8MdEyNWCoR9CuHRAPOY4AhHIsaYsZA3OsQQgggSCYEQJSI0Wzlcl2/ALjsM9Z0q5304OzfISnaTZcx8yUVyoCz3dpQfoctbvFHj6HDj6I62Ib2HljuKURMIkFOld9PxutAQbQAKG6qxnCTwMApud7lCzOk+Kjo9SEUhs5ibx8A99pYQcRhT/DBORCAYigQREEELwTl9Cgm8rSA2GpVFkm8Rw2kLfBfvwR5CGLwoIRzhzpG/ycJTy2AnJf27KMn2oCR72ZRsORyempMtTFzsOinkHmzIF8VG96RYRklPiP6lHJny7VI43QB/uBv8uhltidzzD6A34edBKDAPechACBFGYXtsCy5izmLKEBIIi0fixuKbm4BteUhDkLd507+ScmpSLG+Ld1VS1CY959qsZBAOcXuN2IYbXI/2ENroRQntaAvFq06QBUjENKaCUxSSkD25Cu8Kz0Z3cXPmrrYPjcvODs4bHByb7YAfx9Tgj4kQcPojhl34xQKIuwhEAgwTKhiPHRkkIEZtArOQhhHlh4Ri56rWSZHeYfpnW/IEycD0yC7OdsNczCayWskY3HYz48HSZu0Cu7Fl+HA7xxspovm0Auszd8Fm3ndyrmFSD2p6/ld/zUr9/W/ltayMzf7HvXvfel//CGj8evH7N8vfsHX75pr81/vtO69n/lt2ud2Qd7yxew2z+p0lfFaJq/pN8k7+e90vwnp0UmmbNHAAXajM2s+vF995BoHdKbgux+Mutyhg97q2+5OaG4w/YNvLfO/hqYFdoskT3ZWM0YoVzdHX42/crfFi0zt9lUzL+vu9PFTT5fl6KeTyJEeYRgE3hTTixlER/nh+asvx3AJzx0Gg9jik1aMc0vtZ8scHw4IGDI4FuChC8IWpyZUB3JHAAY1iSmgMJDDRKuazpVCUEwPekkI530cI5582hbJLAEHMREw4pjFjEPGyyAmABSSEF4oxJwhTzD4mSfIwVLclpu45mTvu5fmgCn05RhETIeI8xvFToPpTmS8g3u9get6EOw5Tk4GiTZZ8Ddj3CoZNrxo/n1mHD+1T+wN6DOwPBsHO/UGoW0aL8nLkp7sVYpPLA844PvhQRbvDge4dN/vjM+3no12rCDAimMURwRCa0pi0tx+ORRzDrYjgEAz1Od9zd1OTvjhqwA0wjENwDHBJQCxEy6gjIEBWTBA44wiFjDVRRxxgwVkYQVtGEYvDl8vW4MWx1QppWz7hxlS/oIzRbm6SF8fNQ4UErNj0HqZBxCHOgaCSIMIivPF50XNia/24t59nbT/s++1h3z3l//f37rPbfkO0JA5ady69OBAUPI9gMeZg3pyL+8jfdXHAaN9L8Mqfz4lwN4Xtfz7f52aQVOltjCXawjwvP/wsh7mcW6A7zB1Ey9mdtPyzFy3/dGlhQQyeBkyfweU0BnY+Gyu8Edz2z60+JSvHq9+u2U88m29cX/0fUEsHCCkjpU3sBwAAFSsAAFBLAQIUABQACAAIAJGx9TwpI6VN7AcAABUrAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAJggAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> |
| + | ==== allgemeines Sehnenviereck ==== | ||
| + | Ausgangslage: <math>\ \overline{ABCD}</math> ist ein gleichschenkliges Trapez. | ||
| + | Arbeitsauftrag: Bewegen Sie den Punkt <math>\ C</math> auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von <math>\ \gamma</math>? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck? | ||
| + | <ggb_applet width="419" height="411" version="3.2" ggbBase64="UEsDBBQACAAIAJKz9TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vpbb+M2Fn7e/gpBD0WLrRXeSaHxFE7yMsCkU2xmB4ttF4Us0bY2suRKcsaeRX9UL79jf9MekpLje2LnMhNg52FkkxR5+H3nOzw88el3s3Hm3eiySou86+MA+Z7O4yJJ82HXn9aDjvK/e/XF6VAXQ90vI29QlOOo7vo0IL5pn6avvvjLaTUqPnhRZoe8T/WHrj+Iskr7XjUpdZRUI63rlfZoOkuzNCrnb/v/1nFd3Xa4SV7nkymsUpdTaIvHyZu0ar+e2AUnWVpfpDdpoksvK+KuLziYDp/e67JO4yjr+gy5FtL1yVonNFHTOyrK9GOR12b47eQDaPG8Kv2o4U1k2k5P7EZP9TTO0iSNcrMZawcM8rwPaVKPYEEcwpQ6HY5qs3roZouLokyu5lWtx97sn7osun4Hi4AzSSgOKUdCCi59b+76wjBgGEtGQsE45RgDiGAxmELDgCDBpMSwV4IRh3d2dtml9c2VrmugsvKimb4FeVimycqX19VZkd02TYo0r8+jST0trR/QpumqnpvVALjSbLKXDzPdtBGgaaTj634xu7LAYeqmfjef2FesQf3heZEVpVcaSsD+YfPsu6cdYyxdjEJ2DLIjmjnMpIt+HBI7wj777mlHZWnuTGt2jttdY9Quk1aeaYDJjfsuNp9FfQ3u4HvTPK3ftF/Aba6brWL3wvfTcR90s+w4iznxY815erLmcqfXusx15hwrB26nxbTybowDu7WsIYmO0zF8dR24sc7Q9XcwwLUmeljq1nCnOgeY7UXLzrvWfHrSGmFsqMDWuIbwAfupzV6MumtQVtcfB8PA95KoNq1GPpkea9BWbX3CutQCm0t/EUgKGxNa9Tf9tyhD91b/sJ4UZZNRBC1Bs4EsmkOEWN6Sne/tYFDp2puBFkGzc3BxutR7WSSrMEQ5wGn3CDKemOkNYROtkyZm1o2XexNY0GpmiQ0LYmUWE2YsrNah5sNH97Id4/RlooldlzbkO8DugO7sZ7wJ3qrnLVnzGPA9GUBhAxA6FJ+4GI+jPPHyaAzrnKdlnGkLSmpOEi9CxsO8CDu0HBDTuu2K3XTNJBtwg5en8QLL2F8NMPUIdJzrqrJRsF6Od7vd+R6EoOPpuJdxcFDp/AZMK8rK82aoYWqOWvjblhmg1rFNc9w0fcRL3ADzZTrzeu34XjuqZ45eEYQr/wS002aJHoOZrSh63OQUrWW/5M76ykVHcKQ4HaTxftJ/sKJY5TzeoLq3n+pVZfWOCkqYuKPNPo8PTIxYKRD2HMKjAeMhxlQxzgkmglMXqERAQykoxkIyRiRlD5HlG3DLNYJ6TpSzHhydG1xF+7kyXr6gIjpSlQfHyQfI8hZu1MQ53MS5TZgP0PGaWtIxJMdxWu/n4nVeQ6YBEGwoxhISwcOot93iEitnhyjo7CgFCWYBN4++exwsH+IApvh+hChIyJFSAnPGpLJ+/uju/7aEtGhY5FG2RQhnLe7rcPcPEEH/RYmgg9dO+00SnloFeynp7aIkOYCS5GVTsuVceGpOtjBxue+U0AewoV8UG+unxCJBekL0r/TQtG+XwtkG+IP94FfNbAvkPv/ceRN+HiCFpSQUqZBLJhR3bJCAgzIQC1EoKJWPpQyLb2ZytcUZDfnd5iX/WuuJqa68zd+VUV6Zypwbs1Q8OCbsNWIbbHA9PEBowxcltM42ipejIAqAZSBZcQqJgMJPLsNd6dlwFznn7lp737zs/OiawdG52R784cAPQiYYVwohOGfa2wcWPIBvRmJYKhYKZekgPFCEMRTCaKREW/M7LBu7SKs6yuMd3n++pUoQ9c0byeX5fqDz6ViXS/WC29fMfGDatDVwLbnk9/d0vFEfmk1KcD9zEWyWfadnNazpQU/X//KXaVF/+1Nxo0vjtP9x372/el99D2D8ePmvrxefYef2mxvyq/fTN17X/Ld45XY/3snG5mtY1V8z4ZOKPK3eRO/0P1YjI9hTR2VtKwYOoMs0se7z4+U3nkFgf/1tneLROrUQL+4MbndXNDcYv8e2F8Xe4+sC+zSTRfW6YoxUrGY6X42+dtfGy83w9GU0KapvDwpRzSufb5hi0oUpRgIqBUeYc0oIx/LxotSW87nFZcdBkB5wSqePckof5sgPz4YpDgjkWxIJLAFt3sCNeUCZlBR4oUIS9alLKKnTAt5SQrk4RAcXz1tC2ef/AfhySCg4NQ0RVYCxO6YDAW7OJKcUERIic3wfXyaxf1Zcg/TCQdpzkG5eQ/77235E7d++FojB6LV4zcwfXSH3g50xGkKed9cdZJ/PY3Ro+F6q+mJXecJ7q773cuqojG8xl21jlhUf/qYHmZ5ZnNduFQ+trt+RGq0F+Gevrh9WPr938RzDuphIRUMMDgTngFjoghAmFVeESMZBMA/RxQ9FNoc7266buVUG5GQRbeLLCjHvU5g2vm5O6sge2TC+bz/AG7H9wLp+cvc9wpnRsrSY+elu9vY+AOBzfHRahPYndOt1iujnT7Sf/xcr7uSm/+K46bBASkhUCFccC4VD0ZT1mMQqhK4wJIIogi1VHAUEIRFSrhiVYYjEy+UqfnFcmVCuQDYhR5IpSCSRdLWgjgoQxUogJhnCTDR/C+pgGhAsGJMESQUp0KNVyD8BXcmLowuUxYUAniApxWGbkRplgcwQHMYQ85QiLgh2zG8RRBjCFQGa+WeurHtnxec7s+I/DsqK/1jPiuGeJUIWCqmEYiFnrWs/V1r8OeS923Bvcq6LNufawP3Pg3D/cwvuEstQELiLIIThHH8I7tt+3sWfGnf1hLif7cT994Nw/33bLRDufgrOZKbCUB15C2x/2trEOfN4PuCPcPiT5V9x2h87N7/2fvU/UEsHCEhVilJbCAAAHy4AAFBLAQIUABQACAAIAJKz9TxIVYpSWwgAAB8uAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAlQgAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | ===Der Satz über die gegenüberliegenden Winkel im Sehnenviereck === | ||
| + | |||
| + | |||
| + | |||
| + | |||
| + | ====Satz 1 ==== | ||
| + | |||
| + | '''In jedem Sehnenviereck sind die gegenüberliegenden Winkel supplementär.''' | ||
| + | <ggb_applet width="1008" height="411" version="4.0" ggbBase64="UEsDBBQACAAIAA6k8kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACAAOpPJAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1d+3Lbxrn/O30KjI6n/ySE935J5XZkOYkVW3ZiO0mnkxkPREIUIgpkSEiWfXr+ONN22j5A3+PEzqX3zpwHcF/pfIsFKIIASC5vongS2wEJLAHs9/vuu9/u7i8uzzreRdgfRN34zg720Y4Xxs1uK4rbd3bOk+OG2vnFz3+y2w677fCoH3jH3f5ZkNzZYaZl1LqzIwlFnAdHDa0pbjCmdSNoBs3GEUWM6+NQ8lDueN7lIHo/7j4KzsJBL2iGT5sn4VnwsNsMkvTBJ0nSe//27RcvXvj5o/xuv3273T7yLwetHQ9eMx7c2ck+vA+3K/zoBU2bE4Tw7V8ePrS3b0TxIAniZrjjmS6cRz//yTu7L6K41X3hvYhayQl0GBG2452EUfsEOsUFdOq2adUDivTCZhJdhAP47cjXtNPJWW8nbRbE5vo79pPXGfZnx2tFF1Er7N/ZQT6mWFGuqeQ7XrcfhXGStcLZ027n99m9iMIX9obmU/oseL+k2+0cBeZe3q9/7RFEkPeeOWB7IHAQwl5C9hyi9kDsgdkDt22Y/TmzTZltw2wbRne8i2gQHXXCOzvHQWcAxIvi4z4AN/w+SF52wvR9shNX/cbvQZ8G0StoTBEQ01Lb0Bm9Z/4J+MdQRuWRTuKRpyb9c8eH5o+EJ6jZn0kW6ikdPpTy8jMJr+mnmPBQ2/GZOspHaAuPSv+m/0pPpJO6Of5E+32xBwq2li7u3s5lZTcTD29wYtpm7JOEZwMjMFR7XBu+xx4H4RAS2Jx7WMNBEg/EwcPcYxy+YuUJc5QelXCBedRTnmmHqZdKB1fwPybTmwmPw83MWQlC6WF4EPM49XAqVMwDUfJSwQQhJRRacO5x+JF5PCbmFlR4TMA3qjwG72hkUmJoSOGH8B0eTzyKPWp+jKVHhCfM/TAzsi6UeXW4JfEE8gQ2NwSxBpG24gztlUdNb0RGrijunScFEjXPWvnHpNvLP0Jj0EdX+s7qp4I6fGe3ExyFHTARTw2QnncRdIxApM857saJl2Oo7Ll2P+idRM3B0zBJ4FcD76vgIngYJOHlh9B6kLNB2rbZjQef9LvJfrdzfhYPPK/Z7aDhK3c7eOQzGTIQfKEjF9joBT5yQYx8lpXP7cIV73wQwvO7/UHePGi1DkyLK80AhHwcd17e7YfBaa8bFbuxezu1NrvhebMTtaIg/hx41TzF0MW7Mj5GXeXGhyqav0m333r6cgAc7F3+Kux3oSXWPuNISKmxZJprEOqX9lJDCuQLLOAvVpIho5eagZE9TJAvtSaacZAaLjHY4ZeV1wTS9tHhxRCi4DK86m27Hw15xXw+GNztdlrDy2n/94Nect5P/QZ4h77p1F7c7oQpj6TaFoxy8/Soe/k005v2Xs9e9uAbsi9w1E7p7oFqIBz0ajs7Htlj2sa82bAVStugtAXKuS1qDa9jQ6p2djyyx7QVsK99taynOO8lRvljokGq0NBOJja5sjLMb0z8eRwlD/MvSdQ8zbqK7Q8enZ8dhUMWKt4TL+ueu7fHeGz3NOzHYSdjacDyvHs+sBI6wu2tsBmdwVd7ISNJYOD6DF7Anm2F7X6Yv3gn9ckswdKraJRZS6fTW33Y754dxBfPgBfGXmD3dv6Wu4NmP+oZlvOOwAqchldc1YoGARiR1ujvjAxC15vGWAB5EkMakM7z5KTbT70uUCpwNKLXCc/A0/KSlL1SDh2S+TB13gw9ve7RV6DXhpbPXr8CDC5XslrKlEGndxIYBy/rdCd4GfYLZEjv9/j4eBAm3iXIquH5l+DSsZHLh91WWNCgQQzQpB0EFdBLHUgAvxeGlm9sh+BDD56XiltBiwEcA/Ms7PP0WQ1lPPVX1re3vq2hhZHBwlPt2TK+INXmVdJztw5vZTxniVsic3x+Fvaj5pCQ/ZTQ8Nvz7K7Yz7peIH5RCEa6U0d+NEJ8PJH4V9TN2g06xi33ziJwNhpAorMAiGXAPBqAxUkgMgGmj68iE8sYVxrbUPPSeLfmw0vjmpgPx9HlCOcCM0avQPiCAi9daZwEjOEpePyDVC0mmQJMP9yPWq0wHr7tTLyAqnhhFKRm9+wsiFtenPpg+1G/2Ql3rpyCABmR8AJsALN0P0/yC6f2ZtktSoiDQI7gfTqzYMHvWpHtmLGkWePu7LDPKnPGHTViwNQkmavEhk3GBux2GF/Ae4OfAAEuysLnl8i+nvcqP3MJhG1YfsHZqVd4RCAB4X506e3l7ffyVnvEvL9PNHyk2V33mNEjRrj3wLFR+T3Cr2P7/gNrL4y7Fh0DNBVSfDpFig0xhpAFZUgXEtfJuF0BgxYVgFFlmAsrznTh1WvMIZPjpA4ve52oGSUORD3aLKLOQ1KckRStgqTRWTVJi4rsk9SoF/XYaUmB3Z2swIqewd2FPYN5dBQmKSlJNWh5YGVMjD0zqkZzPIgvKccES02kUESiofkXXGMmOBWKIc7J0pyBuyU1UoTnoeH4Ijp3rZUJSiC1JoNUEJ7W9QpPvVYpk3rNAnEQJxAcAEVKQpGSvVWWjefYXtpzEhL41RQIquXE2OK2PRzZw+IgrJ7v63V6kSx716I7GtQ6OHSi8hhlWiKYkoogSSiWlOBV64m9KXpiNjW+78Kh+wtAgdH8MQaaUVVTYXhWayE540pYBISvtEJECIAFEW3EY0kI7E9B4GnYNuerlfVeCYpwMhSD7G45scNN09cN4jOgMKNccWB3bjJvhtQNgn2qEUEYK6U4pkiuRoOn1OwY52qosQGscpbmNAx7Jj32OH7WD+KBGXsrclU9pGnqrRrQfTiQKlzfvnlOJ0ObpnWGuKXtxwJ87hNgYSQVkkghraaH+9WyyHGKvjmU0i10IgNcqUaL9tLjvqDfvBJDnrvUnU73xZPwuBNepqQvYRmewdub9O+TYWa01KYotV+2A0BhEdHdL0F87Ca6x1P06LokFwJeKTDGWiMQS8mV1FaSgRkkFgi+C4SN5WIi05oc2grCMMVcMYJX5IutQZKrEd6rQ7jthnB7U5RzHcTEBy0iKJNKc0IUz6wiuCtUKQCcE62IyvXMtuF7WML3xA3fk43BF407mCQLnsio/y6ksgAjXwktNMNMMiS0xFsG8N06gCM3gKNNB7gxhnAaob1KIw6lCQEHGNorTqm4QQhPCj7uPSfXNb6UxYJ8gTwSyseN5BLHje5NDQE7L9vduFoHGnqmHuvdkqx8HsEdm6dZEiNIsxnQ8Cj9QO/stJ7jaWGjfXCOzPCG83KiuyBiTkdd3bnDznr2HFcZwfT8jfu7LmL4K/UGGjcMOmVHE7txRrjCUmqFOb5Jln8yLkcbhUsNLKRam2PmKywInIWoj4Mnd3O1+TgsrY2C5f9TEqPac7L2oDL4abr5Ts1NCW9B1SOsJfhAimiJKBc0c47VeKbQyBqFmIhzKYXAjEKUO38uY7MBLqeovnID+KsNAbhGlzZqbFzDycjdRIgz167s0XXcAO5sCMC5Vq5Ryk46+SbiORTZcjx75obo2abEs3hsdFf4fAJoN9GQHtaZ0dgNsnhTIINQYtyOZqFElRlVPhcYCYbMgCghbNtSxId1OrbnBm9vU+CdLYOYRyQ3Ob3kAG/ZR/raDd6vNxze8fxhniFubFGKuGq09nAs+1VW02/fTEtvlcZr8fh4LdCQIVCCQFgEOlIhMXcei6gRjki/ZTyBHRKYFnJaPWg7CWDqMGgrZh20LWYxDf2mJDKrgByJV1Mgyy7S29eOA++vywPvACQ3wsMIwQypYTXROoG8QmqSLV0BUnNJ1n5dVvntt8+JExzfZhn/IhySCII0BOiMgofB54Ujr4Ma17RbAsZ+7qXUy4YbGK83EYwrFcdyq0Y3UsUB9eZQcYcFECtmFr12tFSvqywVgxAaAmgiwOoTTdncpqpuot/sKBJpC7k2wk7NNQtsr1bgfnBC6odpOLEFK77cYbohmu+wAMS956QMxTeOuu+bKt2nqZlWShW40AzjPMxdzOEniG0bHOOjzRWS8cYRjjeVcBBhpl0rQhTWVCylHtIFjhFvW2RD/bkm3TBb9KbCFk2aePHBWqddzFNVNbVqF4JdirFQnHFJKTjxWGYRkU+0VoQLzaXE2tifFZczfDhfjcdGkVMO0/Lzz2VxLKT9wKqRD0vaYzBZdRQLaQfXm5SZK4WylnLYhmI+F0RpjZWZZkDlWG1slQCZStmyAFUmfkbrZt1KVgYlxD+ajHhR3D6aT9wwsQFJepx/4hjLijlXr98ASUEYoxLeGAuqRZ7kU5wwgqSUmjDJ+QrkdTbU7rugdn/emSELwLYSYJQPEqMxQ4QJjrhQqzQ7s6S3P7J69H4Jn2QyPuPp7WQJmnTUvZpWflLydkdHFJnJVDONpWISy2z4QvsCKQr0NaUMJmRKacyJTymTgpnMBabDSLNKM6ONTm4/6SZBMm4mM3gbaciS+tsflPXnT4Ned/AzJy2a/WQeR3CpMjmi8rivNGdEIsGlIpRT63VzH84RyjgDG8Xo/NV+rpTPSJTR/4cp1J8bgw1EAvug3cAtkBysj9IE2xIT4XMOFgeiZMSVEnQVSm4SFEVAXuezmKdAsiAwdfCs2umYgA/1qRIClCFSimiudCYnFM5JCgCBESLrlpNqiGp11oELIAcbRX7lUyMd4D2DG6DxMFHtm2QFpmCbKDjdmOl1IXCQ0/vbCfR2F4ODDWR94TNTjw/8rTSSOqtu1D6jSFMhAQ1pcFkb5cf5nU6h/9wozIbFOrzownRcRaWm2sxEwJoymg/Z+JgJBF4ZNQluqpazpsTseBRReVNvKA4WMxRVP98kaWmAqiISMKKSQSwpdRatYOQTwjAhCC5x0Fb0WgAah6lWeX3sAsrH15og4NYasOpRywpXazzOp5VxPltFnF8TUI7CUsaiOW2EslQ8MHdZyNJnTilfmvDCDPJoJojIBid9DiLCTHk8YyqdTmWmIoO3m7YGtYZAxaFtmxeXJWBL4UtxCRNXtMPNQRvcAsUlVZxpQQXi2QqHcEfBNMcSIYKYRlrhbJ4c8SU22R3Qh+BU022bxlzrqJeF/NgV9uPNgV35QgB8GhS4JBpnQt5gvtCKGqkXoGYZyUBnPga/UWmJFBEITOKWgZ5J+UEJ4rYrxO3NgRiso5bg5hNONFUIZ+sCah+AZ2aJbwX+jpY2BCbaJwoEnisuJIB9c2e/ViN8MFmUT1xxPtkgnIXZEwT+Q5oLkOisbL8hQVGbtBRWZuUalVnsBqU+T/cQMUkQwtW2FXTmsjzRYkeueEebgzcYbGamH0LoyJhgnGcGm5kAhmuCOAYPTcm8kppJxZApp8aUEjop878tcNeA/pUr6F9tDujChwCHgIvGMFdY56v8SR+BhucYLLgG+Rcic9IYuG+aS1AIkkK0RLZNnWeof1zC+NQV49PNwbgxNqSnSJ64kxxJrsBXw2b0NNPjgLEZ6SGCcAo2/ubq8ar5c2P2Ok15lN2zt99PBntsBt33c03lnqUEuG4mN/Ilm8gOI5OAbdqpZib3JI8bX/tsx4MCTjUDS0Xk/uyE3J+vA7lZV4bEdtFbqW8gchPC3TKWZRT/4oTiX6bOwhdVdUaz1+CnS6SMwSjEjDBSm1Tk+KbDWAVgGbq/OkH316kT8+cVwAnI6RmRy6Zl3kDcajP9ucmbLH7/cMLwH9PKNXHVsmOzYFhf5DcVxRuJVBVGZXT+6YTOP+eqwVwYncna8UaiU4FROVB4+y8ndP5VXpqacokwQYQpLQXTC6m/qpmBQs2o/rK1bW+k5/jxTMbq3//tAha0LoPFKFVEE65BoORiXkYVWHJWrGyinWyesZo0WvxgC6o3eL7UHV1S+cYkgj3cAoLpZRNsPLFzFjWral4eWJXwsKQFetNyO2nVSy/oj6w2c93Znc2tfeHppuvFneDSCidb34I2IjVUnf2r5ZCOa/avM+/mQytYrwZl8ywyYSOr2gJtDbAdRq1eRXlMLW6PJqNW1K2PFpLoJRSAlysCV6QiKyeHPShN7X5UoucD91l6+U+u126NmmtCOWdm6yLEOM2yow2QCq5oOvxFiJRqfTO4H4yGFSOztmupPzcGG4aE8LmSSCoslDRLMg9nciMznxhRRAkzs4rVmpGomb86BY8FUdkwbJSPARdtJuYhxRnjw1n2SjAKDzHDhUyvYmpxVTRXkJFHFo8H5WjuN07R3G+WkDV226LNYdEDmeulFWdNzEsuP/qukKQctbpI/LdO2P126rhN1YoVM0C3+NJJjVxYVp3wXwN09QDWwfg7Jxh/NzVzPKcELmOZv2z4rcHZpuM43ZrVTPYv27THLhbs8QbZK621YpRKpShDmOdenZbMzC7F4ElgJMm6DNbjepmpk5w/OUnOn6Yt2SOnjrnMAM5cC/bwfGuezROb8LLXhyeZ/FVGhGfhZaJ3PLhwZ+enX593k5/d+jIl9S3vXc+eSG9SBCOBX+0UbzGZ1o6ho7MkRIOHwbPwl8U4+p3d4y688iDsR8f5+5i9HeGJYieP4HM2SYJ+ki494dkoCZw/LYwLCNEQyUuXmC+Mxy41kphqIguu+aw5zE+2IIcp1pn0/XQLCKZWnfStyud9YrXwpyVle+aazzuryudd8x4OKFvwf1I6T21YOq9aAZNqBTy7+p22ld0sw26LSMiy1a/y00IKwilmJhgdVtEoLOEPN/sBmG1Fa9VvJZlpgczeiKFzIDWdj9T10+GumdTCp0BmMGpm8rtgeEhqSREAIJXQ3NRYu5GaLe5SsMUInR43i9TSJxgzZMbJOYUwnQ252iwhRJVKN5/RjqTmBVLf8W5Rgf73f27NTmh+rZp9fiKjSiI3kJnsTbjSWGqMzDpZMk/eaayYMhWZ2ACBHdUHRuOUxsqN0nCHm0nqOi2NiNCISSbAI1ZqmMDG3KQPtcKCKymKy5HN6vQ9WcaKYMv0+sxGnws4ythfThH9JJo9vd4x+eUEFnx99PpiCwILuU4G+9VWEGyNHLa3jHkQ106yESW2+mh/f0tIxtdHsntbQTK5Ti77YEtItmQum57Zf2pzSk9sZn/vOS4ll96+fs4mZ5dK24iw8Ww+6GaJpBbU7LbKlBZVu4gskmFeznYIU2aLFacOZ4U8Sx2t/MKi8dSisV+FxndOWHy3MiRWu0OSCxJ04sDJfHW1v7JAfLGTbRNSAcTfnID428qAWPXOYauFYuJmCFuh1NWyPfrp3PthOskLWzYm1jqW+PfvTvz79xWr9DJYN517n20B7zaIP5x6sPro6rMto9jq3d7Pt4pi64jgP9oKm2KZa11cdn87aIbXKZkH20KzNfLZx9tBM7ROPnuwHTQb0WertwEPt4NmeJ2+2eG20GyNfPZoO2iG1slnj7eDZkN9tg6f9pPtoBleZxzw6bbQbI189mQ7aIaWzWczrDuWJ+Q+swm5zzMajdRL/N7edcZ6id//mI6bK69/Pwfio7wO9nFFbvTff3AC4w8/5vbnXb40h+N+DscnVXD80QmOP/445jUXGB/nYBzkYHxaNW7wzbRig7GRg28yq7Hdw8GrAORRDshhDshBFSDfOgLy7Y+AzAnIYQ7IwxyQ+5VD9I6AfLdCQLZbZT3MAXmQA/JRFSDfOwLy/QoB2XaT/iCH5JkF5LMyHD84wvHDyhXWzXR3a+oaCmUN7zqUM1xrNcNo2UIWU85Yt9AgPkFcUsQwZTrdbDjPVxGzrTpmDGmuhCaOFSJiXkqKm0pJ7EuEpEBm33lGBVLVhHQsaZLz0lHeXDoSTCgzG14riYGgckhIzKkiRAoJ/3htKc10PbtvtezdbOJmWcu+dtKxr8salgqiqJZCS2o2vJqmYK9SP81u3IpslgZaP84an8/uLSJ/1j0FGrZIqXppmvwnC0/1nEkzQ7+DXtrr9PStt69vzaiwx+uFuxdh37z0f+7d3b/3X7e8aJB4YRR7T8OTOIwvorAfNk99B8XuUE9cjV13ZUI2QxFbQfbQlHpB5nMkBMUUc4RULnfCl0IRjLgAK4CVFG4KTI0B1AmPky8BpMT7Mu23533Zj9on2bl3vVteoU07ABEstrnjpcWG0PKn/4FR8ZZHYTLtjq2wM95m5I4zM4ZalC9qZXrdxY1oikYGtiBMUcaBCzDn+YI6snBaIDy/Pt6z+vhevhbRfkWg7hamlzWyFIJQ8HoZvDHHcjM1MrYjEhP3LF6TSq4f2DjqdjthEA9J1R0n9gjrL7Lk0OwScEVBllXe5hUG1SQsGJvPu/3gfAC/f3Uet7333bnXsi22bEyMW1HO+7ll/cYJynzFKRbgQWoiNJbr5V48K/da0k9UTStm3lGlW3Qovik5FA7A7tcC+8YJ2DcVaomY5Tuo4FgxjByWuFsjsFlIWL323TU7im+m4Fq9GtBhjus4oLHrakCxy2pA1Zi9WJkjUBjsxghDNELBl9MSUS6yLT2B+TgmWgvJwZRb5075XGCzsAwRoFAJ27a9mA/z+G8c/q9d4f/6ZsCPfMG12egH4GeI82yBZWwWwMYES02Mjy8Rz+BXmhBgB2gNhoeK7YTfqPdxBui7MkD/ZjDA6GQXO7G2YcqytxLXcj5n4Irq4GagWiPWjTG5FtnijBBegLrXQjNs9oAVOl8Y9EZwQE0CqJiyP4ySJOz0zuPT5D3vSdCKwtg7B7Z5FkadVj+MwuZp6B2FST9oniRh7JII2mCOqM34NKYv7okI5kSAkWdmo3aUBffKN86A2QFBKySZrA3ua1Apri93NxhEgxdRfBp2vCj2wKuLmieD5kkYn3bMRjTevQwaJ0Aclp+rBuRiQwEB+cRYCgx/sn3XGsYkc6WYElwhLCasQTcxVL+YK1RfH2dfxRxC2Z6DZ1pP6Nk7/mKDchSc2qEhwiZ0bSzQuReFWW7S+yCKQYElJlmRnSnlLCbT4nyDaME0yjYWnJ0Wd8OT4LyXVGZrwMLHA3jV1OCY7+2w2w6P+sHP/w9QSwcICLPUAiAaAAA56AAAUEsBAhQAFAAIAAgADqTyQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAAOpPJACLPUAiAaAAA56AAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAALgaAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" />--[[Benutzer:Oz44oz|Oz44oz]] 20:32, 18. Jul. 2012 (CEST) | ||
====Satz 2 : Die Umkehrung vom Satz 1==== | ====Satz 2 : Die Umkehrung vom Satz 1==== | ||
| + | |||
| + | Wenn in einem Viereck die gegenüberliegenden Winkel supplementär sind, dann ist das Viereck ein Sehnenviereck. | ||
===Kriterium === | ===Kriterium === | ||
| + | |||
| + | Ein Viereck ist ......... | ||
==Beweise== | ==Beweise== | ||
| + | ===wir wissen=== | ||
| + | |||
| + | |||
| + | <ggb_applet width="1008" height="421" version="4.0" ggbBase64="UEsDBBQACAAIAMiN8kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADIjfJAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1d2ZLbxrm+dp4CxVLlxibU++KMnJoZWdJIM5IsyXbKlSoXhsRwoOFmEiONXLk5laSSPEDeI96zOElVzr3ySudvNMAhCIAkwGVIHpcWkEATjf6/f+/+G3u/vOq0nVf+YBj0undq2EU1x+82es2g27pTuwzP6qr2yw9+ttfyey3/dOA5Z71Bxwvv1JhpGTTv1CShiHPvtK41xXXGtK57Da9RP6WIcX3mS+7LmuNcDYP3u73HXscf9r2G/7xx7ne8417DC6OOz8Ow//7t269fv3aTrtzeoHW71Tp1r4bNmgOP2R3eqcUf3ofbpX70mkbNCUL49q9Oju3t60F3GHrdhl9zzBAugw9+9s7e66Db7L12XgfN8BwGjAirOed+0DqHQXEBg7ptWvWBIn2/EQav/CH8duxrNOiw069Fzbyuuf6O/eS0R+OpOc3gVdD0B3dqyMUUK8o1lbzm9AaB3w3jVjju7XZyn71Xgf/a3tB8ivqC5wt7vfapZ+7l/OY3DkEEOe+ZA7YHAgch7CVkzyFqD8QemD1w24bZnzPblNk2zLZhtOa8CobBadu/Uzvz2kMgXtA9GwBwo+/D8E3bj54nPnE9bvwejGkYfAmNKQJiWmobOqP3zD8B/xiKqTw2SDzWazi4LNlp0iX0oObvkyw0UjrqlPJsn4QXjFNM6dQOfK6B8jHaQlfR3+hfpkc6bZiTPdrvi3Uo2FqGuHc7kZW9WDyc4blpG7NP6HeGRmCodrg2fI8dDsIhJLA5d7CGgyQOiIODucM4fMXKEeYoHSrhAnOooxzTDlMnkg6u4D8mo5sJh8PNzFkJQulg6Ig5nDo4EirmgCg5kWCCkBIKLTh3OPzIdI+JuQUVDhPwjSqHwTMamZQYGlL4IXyH7olDsUPNj7F0iHCEuR9mRtaFMo8OtySOQI7A5oYg1iDSVpyhvXKoGY2IyRV0+5dhikSNTjP5GPb6yUdoDProWt9Z/ZRSh+/stb1Tvw0m4rkB0nFeeW0jEFE/Z71u6CQYMnuuNfD650Fj+NwPQ/jV0HnpvfKOvdC/ugethwkbRG0bve7w6aAXHvbal53u0HEavTYaPXKvjcc+kxEDwRc6doGNX+BjF8TYZ5nbbw+uOJdDH/rvDYZJc6/ZPDItrjUDEPJJt/3mYOB7F/1ekB7G3u3I2uz5l4120Ay87ifAq6YXQxfn2vgYdZUYH6pp8iS9QfP5myFwsHP1mT/owTWsXcaRkFJjyTTXYFLf2Et1TV2BBfzFSjKwCQD4sOEZ4cMEuVJrohkHseESQ29vCq5p27f/aoSRd+VfD7c1CEbMYj4fDQ967ebockSAQ68fXg4ixwGU48CMar/bavsRk0TqFqxy4+K0d/U8Vpz2Xi/e9OEbsg9w2ooI74BuIBwUays+ntpj1MY82agVitqgqAVK2C1ojq5jTaIW0fHUHqNWwL/20eKR4mSUGCXdBMNIo6FaLDeJtjLcb2z8ZTcIj5MvYdC4iIeK7Q8eX3ZO/REPpe+Jl3XPvdsTTLZ34Q+6fjvmacDysnc5tCI6xu5NvxF04Ku9EJPEM3B9DA9gzzb91sBPHrwdOWWWYNFVNM6tmdPRre4Nep2j7qsXwAsTD7B3O3nKvWFjEPQNyzmnYAYu/GuuagZDD6xIc/x3Rghh6A1jLYA8oSENiOdleN4bRG4XaBU4Gtlr+x1wtZwwYq+IQ0dkPom8N0NPp3f6EhTbyPTZ69eAweVcVouY0mv3zz3j4cWDbntv/EGKDNH9npydDf3QuQJhNTz/Bnw6Nnb5pNf0UyrU6wI00QBBB/QjDxLA7/u+5Rs7IPjQh/4icUupMYBjaPoixkOHvurEhUf90jr31rk1tDAymOrVns3iC1JtHiU6d+vkVsxzlrgZMncvO/4gaIwIOYgIDb+9jO+K3XjoKeKnhWBsOEXkR2PEx1OJf03duN2wbfxypxOAt1EHynQ8IJYB83QIJieE0ASYvnsdmljGuFbZhqxXxr2N6cujD2fB1RjnAjMGX4LweSleutY4IVjDC3D5h5FaDGMFGH14EDSbfnf0tHPxAsrjhXGQGr1Ox+s2nW7khB0Gg0bbr117BR4yIuF42ABm6X4ZJhcu7M3iW2QQB4Ecw/tiYcFCFcSKk5jT84GnU8jPppMfbLPffQXjAF8AglgUh8hvkH0858vkzBXQrm5ZAsenvsRjMgcgDoIrZz9pv5+02gcnRrlEwyca33SfRVJrPnEjx7HZ87/o2scfWotgPLLgDIifI6cXM+TU0GIEipcFbSGBnA7bNS5oURYfV3eJOFrSjz9GBambJLV/1W8HjSAsQdTTzSJqFZLimKRoFSQNOvkkTauqp5HZTmuqi4yKOpiuotK2/+CGbD+2Smq6jpoDtpmGn7oEKUk0okIyiYiwytGcFlQhrZVWlEiTGFiSV3CQ0TZpFI+NYKRBPLDmxstg2ZyOZUrGmjcrY8XKJ4fWaxaco24IYQKQJCM8Ed2bWRn6HNtL+6WECX41A4N8eTJZopY9nNrD4iisnvGLdX+aLPuVdExlmowFGJRFg6ZTtcw440qNiURaUMKJllSuXFnsz1AW86n8wzJcerhWlb8SpU5cwQmmVFGNBOaEx0BhlwiMBSZMaE2Z8SOXhNPhDJye+y1zPl+v72cA86cDNozvlkDib5pqB4ecYcm4QpIyzRC3ElGXruSYaAwCJDRCVK1G00e0bBsGGWl2gCqb17nw/b5JqD3pvhh43aGZrrNtxvJFBYBGybp8OA/hQPJQffvNdFijNNAIM2g9kQ7gLmGYcCUFkA4TzGcmB/JlleMId3PISCudCv217rQ4q2mSXCWE9AaNawHkiXvebvdeP/PP2v5VRPYMjn4Hnt5ki5+N8qiZNml5/XXLAwwWEdrDDLxn5YT2bIaeXZfMglbUDNSlBtE0BoyxOEGAXM4F13BWCmUS3zgSYuYybvwFRTmSmlO2tTKcj+9+Eb6tcvi2NkUpFwGMXSWQEkRJ0NMAsNXR0uWIK1AvkgqExWgeYdfwPcnge14O3/NNkV9wSzPuZwTvhINPE/GlYJjhLzRmGK8o2LoxeA+K4A3KwRtsOLz1SXy5sj4WdgUCtxdxDd4vRlhtkwBPC0zu3tQ8VBzn8VzAkpl8M6WRHldedhDQWd780t2ZwWH7TavXzdd/d62XepCRk08CuF/jIk5weFGmAxqeRh/onVrzczwrnLTdJriMbliVC8vbUMzpuItbZQJsRgpjUl14s3M75Z91EZOfqzTQpE0glhuJi7BmELBxhiEqgwB5a3XGJDCnGwVMAS4km4yLdIRAQkLExwWmkojtVeSToDQ3CpT/P1mLfJfpblHE0yjnMjU2x2UiVCkKgQ1FSEC0qlXsEmfzgpH2k1giCpEu5lopUT19scnwZvNRL8vB+3JD4C3QofUi41YvZd22EeHYpcv6cu1yCLc3BOFEIefr4zLqeBvRvFsUwXbKodnZEDTxxHwvcrfJkZkHsZMiA9oth1h3QxAzuYWUAcVx9JBrPpmLkUKYgG4VQmg+zX5uMbpZ7dovh25/Q9CdM18Y55O2Op1UAt6se/RFOXi/2Gx4M/nCOB9c352EcN6c7Ekq25XV0G+/mZXOmpyVjUPXsXlZ5GqitAAnhWNGGNA8J281Dy9gosa4IfoW8wMuka2MF6Xkz83iKejSEnOzYt652XTK0pBvRtYyD8VRhBqhmPWM3n79OS2FommfRZERIcG3RIIgpLhaO4rXME0TwhXAVEmmDosyyG+/LYXFt1kkJPj2RoUhqTQosopAJDVRk8p1R2A4TPySYqEgJYWCzIJCrRuLa8WWLEvAdCMVGxCvgmI7SWGYs2To65Lm6es888SJUkJLqQUDD56TihhaVwWj6hgSO5PGNsI2VVrctV8obT+UwumHmSitGaQtUXonKRjuZmH4qhQMX+X5cogY629CXIrzCvDKuvUEsV2DIT2JnCMN35S0Pd/k2R4wOtFyXa0p4kisGYoxn1pwa3uY2ATFleNUZ23PtJUUH97QEu/5y61mLvFmrmBKQLjFEdWIIZEEuYxx8OAJxZgJuC5WXr5wr1pNx0ZRU44S7mgp9JqjhPZDq0HuZVTHcLreSJfQDm92kWWlJMlaqmSFS7Ti3NgxJTUxSaB0yWyOAJkC2hwByk3tjNfTlitPGWYQvz8d8bS43a8mbpjY+CM6Vl8KxuIiz1ULpPEGCSOKcWayc1wnU5yKUoQVwVgphaVUKxDX+UB7UAa0B1VXeyyA2kpwUa4y24ZhDsRXmnG8UrMzT/r6vtWjDzIAhdMBmkxfh0vQpOPe1axSkoyjO878pkQL/HCsCVeMCrt6wxT+y3hpOmdK29lg4XJoyZlASAqpk2RRrmZGG52+ftYLvXDSTMbw1iFSiVztD7Pa8+devzf8RSkdGv+kihe4VJFMlexRoZnmVIDBYoKOrYsTmnMJgGNUfe1sWbLHFIqJ/8MM4leGYPOAYK7k4DdQhBgWYHtwDIQkoO04CB4GgJQR9LUikcbj62RV8gxEFsSlCJ1VOxxT4BGuYkwrqaTEVGqsY3jM9miESyRN3Q4V6xaUfJBIEUhHZSA52igAlCuUNKuShKZSEiUTz4yBW6CVMue5yVasTUKOEoJ/W0ju8nJwtIG8Dw6AAr7X3KxCYLFmqlOXKSIQoxoCGsSIXB/hJ/mdzgCgMgzzgbEOJ/oaDe5iCiJgagi1BNfLosFdDvEmSIYyFYeCyTWDkYbkm2I7cbSYncj7+SbJCnaFWYkAd0OYaJY4VBD2UxAews3SSYko5muzFHkUG8FUaCkelgHl4Y3mBuKN1Vj+/GTOOp1UiC+wzI3xhVhFjF8QS47DksWiMWsuMlMQULnMY+mroqgrONgGLZUSlMtog1Ob8MRAYiYxowjkhIq4iJK5SJrtXsHSm82/p2X4N3tRVD7ScfY1E76kdyEpi7e/OXiDosMSIWJSoBSZbYDjJawYCS3MwlYpwXzF2k+7nGoGbKAUZaA4t6n8rYRgZ3VvVsjPyoJ+tjmgU5eDoTNvD1AgtSTJzkF0pAWFuIiYlY8cxwsfAXUBfiNRFNxKLfCugR7L+FEG4lZZiFubA3Ed7CDYSwzBLwMLyYXdwgvUNYXQCxwapZUAs2nlGrlCR6uXtAB+MOK+WxAfTZfl87JAn28Q0GCaqUSaYcEppQon61pdAZG2WSCDQWGjOBHFXIIgCIHwm4AdB4W/Y0AnsjzVXgdl4Q42B24w1wy8Yck5Q5KiUb06gzBFMGomMiURlMWqW4GmB5+NKC6BPaTa3kXr8+NdgPrLsqi/3BzUiasAbMxB0kFPSzRK6SDgBR05cALpxCeXriQSg7lmmEuJdq3OKMb8YQbhi7IIX2wOwvWJyTwmVZKIwERgkF/NNTflJxZk6mIsIeKCaM1kKDTfXq8sb93chMGOkh5ZB+3t99Pxnlg79/3MBfRVVzEWrdqGDthUjhhb8huX3udnRabpbXzjqxyPUjgVzCylkftrKeT+ehPIzbvFI7baOHnbzVYhNyXgzWKZRfFvpVD828y13FULwuLF3GbPkwkUhZgTRWr9Zo63HcU8/LLI/b0Ucn+fidxii45zkdNzIhcvydxC3ApT/YnFmy59/yyF4T9nlWPSqvUuxYV8M1HcSqTyMMqi869S6PzrBsosZ2rHrUQnB6NsqPD236XQ+Xd2i2kqBRIQeklw2pFCi5Uh5S0LFGpO/Sf19nqOD+eyVv/9nzJoQessWoJoKczecMIkT5YOlpwXKzt5STbPWk2bL360A6UbPNm8ji6pdmMawY53gGB62QSbzO10gkZewcsjqxKOM1qgPyu9E5W89L3B2FYyN53g2dzCFx69bD1d6yKT18PR5BYbmQAs5JB22QRgu+qbhlawGw1KJuissJFVvRdtDbCdBM1+TnFMIW6Pp6OW1q2PF5LoJRR8Z8sBV6Qic5eHPcqs7X6coeej8uv0kp/crN0aN9dmRybGCISlWHHKkwIiDd62YkRJLAQER6soIMqne8Gi7ULqV8Zgw5AQrllIjxFG8L8ibFRBjCRgwM0ib86Zrv6OqGpAFCxgnQHHgqBsGDTKJRgpLBQiSGqKRjuYMThrJgUZMYv2VoBMXiyXkpDHFo5H2Vjut6Viud8unjOeBscim7TUkym6grdvLi2aMw+5/NA7R44S0IrC8N+Vgu53MydtaDXoFt8jqc5ie7LqdP8aoCsGsAjG35eC8fcz88Z5r5+YqzBv8V384rm3+mj6e2NxnG3LCtb6Zy3akzL268kGWSuttSKIISmI5iJ5v7qrJcXGtxCgEjRahUeXJ0RPikWmSHD+XEpw/jxrox4+c5O4ObCptFEPj9Wf3Dyp8a/6A+jJ5K5iIrzwr0LwLuHCndrPv7jshb+49euI1Lecdx17IrpJGowQflVL32I6rUuGjaUFIRgeey/8X6Vj6Hf2znrwyEN/EJwlz2Ne0Ag9ghzE0XuiX0NvEEabTjg2QhKaaoHhfyIl0aP1QkKCeZWG1agm6Z0v5s1fPt2B/KVYZ8L3ox0gmFp1wjcvl/fUauGPMsq2UzaX18nL5d3waxlQvPXGtFSe2rBUXr4CJvkKeH71SxYHZyEJWbb6VS6D2BoTs/chERCPJuoXIm/4YwrbkRKKFarfXDLTFJmdMUNXgtS0GqmLl8LdMKmFS4kpTlOKCSIYHpHarIkmXCqhOdWcliM1W9ylYIsROjpuFqmlSzBmiDNJOaWIsRFXUwbBu4Kw3axQLklqniL1HecWFeg/f7k1P6H5jWr26kRGuUQ2m2AwSbjSWGps1nAjOUpvY8WU4kxjAwQuqT4wmqQ0VuUoDXfYTlIXaWlkKviZZEKaiYNRhhRzDUEoRJ0mgy2IrOIlP1vGVmDL9PrMWzsXcJQXeefqvDR7frPz8csJLPj66PXpDgQWcp0M9tlOEGyNHLa/jDUQN06yMSW2+mj/cEdIxtdHsrs7QTK5Ti77cEdItmQum53Zf25zSs9sZn//c5xJLr39enpuafJlIZOZfNDLEklt3qwpNVNaLFj+sqK3UMxYJZZeMhwvil7qROWnFonnFonDPCS+K4XEdytDYrUvQSqDBJ06aVKtnvYzC8SnFoi7eUD8oxQQ/1gZEKt+LdhqoZj6BoSdUOhq2d78bO69F63uwpaNibWMGf79sRT//rhilZ4Fa9u598UO8G6dJN4IWUNk9fGOUWz1Lu8nO0WxdUTv93fCpljmWheXPdgNmuF1SubRrtBsjXz2cDdohtbJZ492g2Zj+mz1NuB4N2iG1+mbnewKzdbIZ493g2ZonXz2ZDdoNtJn6/Bpn+4GzfA644CPdoVma+SzZ7tBM7RsPptjw7EkIfexTch9EtNorFbiD/auc9ZK/OGndFylvP6DBIj7SQHsk5zc6H//WAqMP/6U26+6bWkCx4MEjqd5cPypFBx/+mnOqxIYDxMwjhIwPsqbN/hqVqHBxMzBV7HV2O3p4FUA8jgB5CQB5CgPkG9LAvLtT4BUBOQkAeQ4AeRB7hR9SUC+WyEgu62yjhNAHiWA3M8D5PuSgHy/QkB23aQ/SiB5YQH5OAvHDyXh+GHlCms73d2CmoZUScO7JUoZbrSSYbxkIY4p56xZqBOXYIaQEkhyirSMt6Y25xWGk4poRIFfGClXHSKqUlJsKyWxK83rzhGX5sV1AqkCQhaXf+QSUlYlpNxeQpp9G4TSlClKCWe8gJLlCKlShCTOQdu7dN51iHMctL3ow7NeGB3vD/73x+78hFabSWg0W/SZIJQzRpRQAjMtRptkYNAGwMimbgkzyUsWhqW16IH/2m/5Xed54Du3DhznlnMJRvDWYZlCsZtVryULxWYRnpk36SjKuHmdKOd4pCj45Ol8qoPp7w6hw6gA23xv+b2WfzrwPvg/UEsHCNAORgQMFwAADdEAAFBLAQIUABQACAAIAMiN8kBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAyI3yQNAORgQMFwAADdEAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAACkFwAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | --[[Benutzer:Oz44oz|Oz44oz]] 22:55, 17. Jul. 2012 (CEST) | ||
| + | |||
| + | ===zu zeigen:=== | ||
| + | |||
| + | <ggb_applet width="1008" height="421" version="4.0" ggbBase64="UEsDBBQACAAIAIak8kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACACGpPJAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1dW3Pb1rV+Tn8FhuPpS0N43y+plI4sJ7ZsyXZsJ+lkOpOBSIiCxVtIyJYyfTnTdtr+gP6Pk3svaTtzzrv7l87a2ABFEABJgBeRPMlEBkls3L5vrbXXWnuvjb1fXXXazmt/MAx63f0adlHN8buNXjPotvZrl+FZXdV+9f7P9lp+r+WfDjznrDfoeOF+jZmWQXO/JglFnHunda0prjOmdd1reI36KUWM6zNfcl/WHOdqGLzX7T3xOv6w7zX8F41zv+Md9xpeGF34PAz77929++bNGze5lNsbtO62Wqfu1bBZc+A2u8P9WvzhPThd6qA3NGpOEMJ3f31ybE9fD7rD0Os2/JpjHuEyeP9n7+y9CbrN3hvnTdAMz+GBEWE159wPWufwUFzAQ901rfqASN9vhMFrfwjHjn2NHjrs9GtRM69r9r9jPznt0fPUnGbwOmj6g/0acjHFinJNJa85vUHgd8O4FY6vdjc5z97rwH9jT2g+RdeC+wt7vfapZ87l/Pa3DkEEOe+aDbYbAhsh7C5kf0PUbojdMLvhtg2zhzPblNk2zLZhtOa8DobBadvfr5157SGAF3TPBkDc6PswvG770f3EP9w8N34XnmkYfAmNKQIwLdoGZ/Su+RPwx1CM8thD4rGrhoPLkhdNLglXUPNfkyz0pHR0Ucqz1yS84DnFlIvaB5/rQfkYtnCp6P/oL3NFOu0xJ69ovy92QcHW8oh7dxNd2YvVwxmem7ax+IR+Z2gUhmqHayP32OGgHEKCmHMHa9hI4oA6OJg7jMNXrBxhttKhEnYwhzrKMe0wdSLt4Ar+YTI6mXA4nMz8KkEpHQwXYg6nDo6UijmgSk6kmKCkhEILzh0OB5nLY2JOQYXDBHyjymFwj0YnJYaGFA6E73B54lDsUHMwlg4RjjDnw8zoulDm1uGUxBHIEdicENQaVNqqM7RXDjVPI2K4gm7/MkxB1Og0k49hr598hMZgj27snbVPKXP4zl7bO/Xb0EW8MEQ6zmuvbRQius5Zrxs6CYfM/tYaeP3zoDF84YchHDV0XnmvvWMv9K8+hNbDRAyito1ed/hs0AsPe+3LTnfoOI1eG41uudfGY5/JSIDgCx3bwcZ38LEdYuyzzL1uD/Y4l0Mfrt8bDJPmXrN5ZFrcWAYA8mm3fX1v4HsX/V6Qfoy9u1Fvs+dfNtpBM/C6n4CsmqsYXJybzseYq6TzoZomd9IbNF9cD0GCnavP/EFvv1bXyOVMU0KQAtPCEFif62QXcwUW8D9WkkGfAIQPG55RPkyQK7UmmnFQGy4JKNd1wT7O7cX91yOSvCv/5nlbg2AkLebz0fBer90c7Y4QOPT64eUg8hzg/gbmsQ66rbYfSUlkb6Fbblyc9q5exJbTnuvldR++IXsDp60IeQeMA4Gbclrx9tRuozbmzkatUNQGRS1QIm9Bc7QfaxK1iLandhu1AgG2txY/KU6eEqPkMsEwMmmoFitOYq6M+JtO/rIbhMfJlzBoXMSPiu0BTy47p/5IiNLnxMs6597dCSnbu/AHXb8dCzVwedm7HFodHZP3pt8IOvDV7ogh8QxdH8MN2F+bfmvgJzfejrwyC1i0F42La+bn6FQfDnqdo+7rlyALEzewdze5y71hYxD0jcg5p9APXPg3UtUMhh50I83x44wWwqM3THcB8IQGGtDPy/C8N4j8LjArsDXK1/Y74Gs5YSRekYSOYD6J3DeDp9M7fQWWbdT32f03hMHuXFGLhNJr98894+LFD932rv1BCobofE/PzoZ+6FyBthqZvwanjo3tPuk1/ZQN9bpATfSAYAT6kQsJ5Pd938qNfSD40IfrReqWsmNAx9Bci7o8uladmA9fWu/eercGC6ODqavaX7P8glabW4l+u3NyJ5Y5C24G5u5lxx8EjRGQgwhoOPYyPit240dPgZ9WgrHHKYIfjYGPp4J/g27cbtg2jrnTCcDdqAMyHQ/AMmSeDqHPCSE2AaHv3sQmVjBubLaJfAy80Ydr45yYD2fB1ZjkgjAGX4LyeSlZurE4IXSHF+DzDyOzGMYGMPrwMGg2/e7obueSBZQnC+MkNXqdjtdtOt3ICzsMBo22X7txCzxkVMLxsCHM4n4ZJjsu7MniU2QYB4Uc4/tiYcVCFdSKk1jS84mnU+Bn0+GHztnvvobnAGcAolgUx8jXyN6e82XyyxVgV7cigeOfvsRjOgckDoIr5yBpf5C0OiAmLIDuHT7S+KwH4MDUI/09AO/F6K+9mS+69v6HtkswPllwBujnKOrFDEU1YIxY8bKsLaSR03m7IQYtKuPj9i7RR4v9+G1UULtJqP2rfjtoBGEJUE83C9QqkOIYUrQKSINOPqRpW/Us6rfTpuoiY6PuTbdR6c7/3i11/thaqelGag7aZvb8zFVIcQUBgeKIEEoTP0BrKZCUjFGhuEDLcwvuZaxNmsVjoxhpEu/Z/sbLcNmczmVKx5q3q2PFxicH6zUrzlE3hDgBIMkoT4R7M6tDn2O766CUMsFRMzjI1yeTJ2rZzandLM7C6gW/2PanYTmoZGMqYzIWYVAWPTSdamVuICMu1phhhQlmWkohxMqNxcEMYzGfyT8sI6WHazX5KzLqhAlEKGESY6yVpbmOXYo5JZJSxblUhC6NpsMZNL3wW+b3fLN+kOHLn87XMD5bwoi/aZYdNEJgiQWVXCLEmDDqCVDXpasYJxRRJoiUdFWWPgKzbQRkZNmBq2xi58L3+yaj9rT7cuB1h2bAzrYZSxgVMBpl6/L5PIQNyaP17TfTeY3yQCPSoPVEPoC7CAAVEqwMI5olybnS3QnHEfFmk9FWOpX7G9tpiVbLjiG9QeNGA3ninrfbvTfP/bO2fxXBnuHR78Ddm3zx81EiNdMmrbC/aXnAwSJae5ih96yc1p7NsLPrUlowi0IRohBD4A4gGY29XkcROhcgHEpQTDUiTIlIiYXLEGgu0YIqwuCArdXhfH4PivhtleO3tSlWuYhg4iIO3STHhAvMCJYy4lcbG80UQogozcA73E1+TzL8npfj93xT9Be5LON+RuEVTTv4tg+GTgTDDqwQ5ozzUXZ9V+i9V0RvUI7eYMPprWf4tS4WdsE0KyK5RlqAAd8qH2taXHL/tsahqLRjF6uOWog7YnZ5AeT9mQFk+7rV6+bbyPvWk72X0aVPAjhf4yJOgnhRNgQankYf6H6t+TmeFXLayybkjU5YVVTL97MQCo67wVVGyWakOSZNijc7/1P+XhdxC3INC8rvNyCmRkJpcBMURCCS4601K5O0nG4ULQWskHxrj1yiMGaCM4qFAl+Ob1N/Pp2X5kbx8v8ot5HvWN0viosa5RyrxuY4VlgxIYmA6MeEP0Kr2HGW6eyh1TXqIoWAeE4YkZRhlZkbVWKofIMJzuatXpUj+NWGEFxgSesFHVy9TA+3jfzGTl3Wm2uX47e9IfwmFrnAIJexx9tI5/2iQLdTjs7OhtCJJ4aF63hVMyhujbKToi60W46y7oZQBhSlu1AZRxC5HahwEbiqmDBKTH5CbVMEUYLdrH3tl2O3vyHszptXjHMVW5x2KsFu1jv6ohy7X2w2u9m0Yuwd7U7eOG/o9iSV8Moa6LffzMpoTQ7exsHr2PAtcpUGvKmWjGumdE7iah5JwESNyUL0LZYGXCKnacmm+QO40ywzLTGAK+YdwE3nLA14M9KWeRyOAtSIw6xf9Pbrz2kpDk37DIcaHEoimTIjn0olhUhrZPGGpmkB6ApoqqRRh0Up5LffluLi2xxtUkwisEWRj0F0VX1KSqcmbeuO8HCYeCXFWkFKagWZwUVVnajKxI1dY3FxA6YbadcAugp27STFYM60oq9L9k1f5/VNVFAqIWIWEEIrcN7zSo/md1Qwqk4isVEE24i+qdIMsINCZfuhFFE/zKSJVNW1qjRtidU7SRFxP0vEV6WI+CpbmocQBLxYc07AhdZyIRri4WnEdo2G9Dhyjj58U7Lz+Sav89FKgToYd8wkAJPK57VxMeZWiziIYmITbFeOX53tf6ZNufjglqaCz1+WNXNSRTTpG0OAy7iklCqKZRz6uOAyKsKF5lJiTeTK6xw+rFb8sVFwylHOHS0FrzmKbT+wNuTDjPEYTrcc6WLb4e3OxqyUJllLPW1dMTPPV2mNFZcCm9lOqeLaPAUypbZZBcpN7owX3parYxlmGH8wnfG0uj2opm6Y2CAk2lafNMbiatDV2zdgUhDGqIQ7xoJqkeTxlBmpRlJKTZhZtGT5+jofaw/LsPaw6pSPBWhbCTHKBY3RmCHCBEdcqFV2O/MksB9YO/oww084nZ/JBHa4BEs67l7NqjnJuLqpEX4mGWIaQ0gksbTRP9auQIoCvqATQmhB7MRn4lLKpGCSCILpKLzMs8xooxPYz3uhF052kzG9dYhVImf7g6z1/LnX7w1/WcqGxodUcQOXqpFjBo+71Ng10CopaLQmoZmc60rEsMSIaoW54GQFapUPe4xQDP4PM8CvTMEGEgE9jMAKjBulXHHB4nnSZn0OwpAiGnQNIynWTEWakK+TuckzKFmQmCJ6Vu1xTJ1PISShRHAB/2mOEIvpQZoTKczyaFogrW+FnkmSSBFJR2UoOdooAswEJKk15xhLAWoikunVjFKzIinCSEiExdoU5CjB+9tCtMurwdEGir50KQg2lSDejGqdZGWUi6TS4ANQxagCt2FtwE+KO51BQGUa5iNjHT70+EwDIhH01lQpBB4x0UomozQuIppryQQjHKKUVcQo0whJ0/JNcVdxtFhXkXf4JumLmbuuCBYIM6EE0VQlk0GQK5gCN1ohKuUqYpXZ9EySVNhVPCpDyaNbzQ7Ei7Cx/GHKHFdrMsinuUE+XWM0OU5LlovGrCHJTFVA5WKPpc+M0i5CpteQlHMluQ3cmYsM9NosFK4FM6vRmqWLuIs4RiAF1EwaV9NWPtjsSVH5LMe510zwkl6tpCzX/uZwXTfV7maWG7gLDNPESTZrH3CEpYYYE1hXmMRTkpkrCWcYK60VbMSO8V3oo2c1/Kws62ebw7p2qQa1xRoxJBQiN+s4KQZqjiB8haCWknh5Mgbuu1awz8yUJMlY786QHiv5UYbiVlmKW5tDcZ2C50Ix4xqBEQenRlmStYu5Bs610NiQPLLjpnBEgXdKCQHF3jGKj6br8nlZos83iGgwyRK4BF0mQggcrdweBXsCPFpCkRAmEayta1Sn0BwrY8KFmbmhd4zoRJendthBWbqDzaFbQwespcRSKKYkxUnJJleEMqIYpxr8MxznVCRY9GixN0xMAobvWlFCHt0FpL8qS/qrzSFdupSBzgqMFEIcxeM8deFyiZiEmFVzos1KVNZJIy7YAgY9OcccgQDsaIf9KMPxRVmOLzaH4/rEYJ62HIO+A+Gg3RzccMLFyIojyUDhwTunhJvOfVspzps2N9FdR/mOrHv29vvpZE9Mnft+1qxtlLeUyiLztk0d4JwZERLb8fyEyLQ5jvjWJzkepXgqGFVKM/fXUsz9dc3z7YG3eZeBxNbbGvlR28TblGA3y2SWw7+V4vBvs6ZyLziR26x4MkGiEHOSGK/9PFrwYGtJzKMvS9zfSxH399lz8JfPnJ6TuXgy5hbyVpjiT7q76cr3z1Ic/nNWKSYSFTksLuObyeJWMpXHUZadf5Vi518ziyzVKtiZbh23kp0cjrJBwtt/l2Ln39lVqM2b8BQmBFxGzVlVr7F4PqBQc5o/qbfXa3w0V2f1n/8qQxa0zpIllZaUcqwRQXr5ZMl5ubKD/mTzOqtpw8SPd6Bmgycr19ElFW1MA+x4BwDTywZsMqnTCRp5lS6PrUk4zliB/qy8TlTr0vcGY4vI3HZmZ3MrXnj0Qvb0C+SiuiZb1YI2Ii2Un/krlJB22cxfu+q7iFawEA1KZlhYZSNbvO7XSdDs5xTFFPL2ZDpradv6ZCGNXkKtd7YOcEUmMndW2OPMnO4nGTwfl5+clxxyu/3WeHeNKeLgs2EzK5Kq5H2dLlEaUyw1lVxjrdYGe8Fc7ULwK1OwYUQIlwousZZMK0640smcO4xMBYrAykyql2xttSaPs1He2KzVGXwsyMqGcWOmcnOtzdrXRAopxt7wxTCEOQRRzgiu/oavcsFcSkeeWD4eZ4O535UK5n43M/Ooq6atqvYIY1NYpZr6HuGlBXTmJpcffeeoUkJbUST++1Lk/X7maFvVtPHiqyTVWTy9e9UZ/zVwV8xgEY9/KMXjH2amjqsuN7KMdfzi4bf6aNX/jSVydodWMM8/2609LdOJPd2gLktDh4XAdxCKKq31aNKpxCBO3JSLE07wKsrB8tToabHSFKnOX0qpzl9mrtSz2JhnNhs5v+Lw2ALKzdMb/6o/gCuZFFaMwkv/KgRpgR37tZ9/cdkLf3nnNxHWd5xfOPaH6CRpNkI4qpY+xVJ9hdKqEAyPvZf+r9Oh9Dt7Zz245aE/CM6S+zFvcoQrgiLEQXyStQ69QRitOeHYQEloaub6aUqkJPHbG+rMFRIkTIKVxlQTmQqU5k1jPtuBNKZYZ973ox0ATK0675uX0ntmzfBHGWvbKZvS6+Sl9G75zQwoWfl9ikVVG5bRyzfAJN8Az29+yeLkLKQhyza/ymXYzLfnEHITIbRMzK/C4NBgjkyVnFCs0PzmwkxTMDtjHV0JqGk1qIvnw90y1MKlALNxm5ggguER1JKaqkSphObgQdJyULPFXQq2GNDRdrOgli7BmEGYLimnFDE2kmqzdhBVygyjY10Sap6Cet+5QwX6n/++Mz/Q/FYte3WQUS7I5p2mTJqUKjalO2aBrGRJAFdjxZTiTGNDBC5pPjCaRBqrckjDGbYT6iIrjYjQUZUEeMQqGU3AURmcWYoMC66kSK9DNq/T93wZS4Et0+szr+5cwFFe5MWr82L24naH5ZcTWCzhRbXz4vXpDgQWcp0C9tlOALZGCTtYxlSIW4dszIitPto/3BHI+Pogu78TkMl1StkHOwLZkqVsdmr/hc0pPbep/YPPcSa59Pbr6bmlyTeGZN9/wCWSWlACbiVTWqx7JHq+ZP2MyWLpmcPxQN5Sxyo/tUy8sEwc5jHxXSkmvlsZE6t9D1IZJujUQZNqJbWfWSI+tUTczyPiH6WI+MfKiFj1q8FWS8XUNyDshEFXy/bmZ0vvh9EkL2zFmNieMSO/P5aS3x9XbNKzZG279L7cAdmtk8QbIWuIrD7eMcRW7/J+slOIrSN6f7ATfYoVrnVJ2cPdwAyvUzOPdgWzNcrZo93ADK1Tzh7vBmZj9mz1fcDxbmCG1+mbnewKZmuUsye7gRlap5w93Q3MRvZsHT7ts93ADK8zDvhoVzBbo5w93w3M0LLlbI5lx5KE3Mc2IfdJjNFYscQf7VnnLJb440/puEp5/YcJEQ+SOtinObnR//ypFBl/+im3X3Xl0oSOhwkdz/Lo+HMpOv7805hXJTIeJWQcJWR8lDdu8NWsQoOJkYOv4l5jt4eDV0HIk4SQk4SQozxCvi1JyLc/EVKRkJOEkOOEkIe5Q/QlCfluhYTstsk6Tgh5nBDyII+Q70sS8v0KCdn1Lv1xQslLS8jHWTp+KEnHDys3WNvp7hbUNKRKGn5RopThVisZxksW4phyzpoFs9YR4pIihinThAlJR2sgmXepY8aQ5kpoUrI6RFRFUmwrktiVCEmBzMvmGRVI5QNZspxJVsVRbi+OBBPKJJh3ZV4+k9QrAZDYrNFlFiGCP15cRpMLpKoKpNpMINEchYxIIc2YwEJxPcrbMEDXrKjCtCbRz6WKvqpbyA01kbNxVIxQyoVE3IBZgCMrXvsgH0hSGcglVDffBpDmzULQ0XCOhDav5WZLAjJdxvxg8L8/dp1fOM97Ifx7HLQ92Nxre5clAK5Y03zbAAuXEAx2E2NpXgJ9A7DiprxTUo0oZais4cTp4uV7/hu/5XedF4Hv3Ln3rnP47v0yJZ8Vy5iXhG3Jks/ZiHMilGQSUcYUQM6TRS3gdxBxQjTDYDSKIQc3vjuES0aLKZjvLb/X8k8H3vv/B1BLBwj3kJcObRcAAATVAABQSwECFAAUAAgACACGpPJARczeXRoAAAAYAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAIak8kD3kJcObRcAAATVAAAMAAAAAAAAAAAAAAAAAF4AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAABRgAAAAA" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | --[[Benutzer:Oz44oz|Oz44oz]] 23:03, 17. Jul. 2012 (CEST) | ||
===Beweis vom Satz 1=== | ===Beweis vom Satz 1=== | ||
| + | |||
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
!Beweis 1!!Beweis 2!!Beweis 3 | !Beweis 1!!Beweis 2!!Beweis 3 | ||
| Zeile 42: | Zeile 92: | ||
| [[Datei:Sehnenviereck_Beweis_1.png| 300px]] || [[Datei:Sehnenviereck_Beweis_2.png| 300px]] || [[Datei:Sehnenviereck_Beweis_3.png| 300px]] | | [[Datei:Sehnenviereck_Beweis_1.png| 300px]] || [[Datei:Sehnenviereck_Beweis_2.png| 300px]] || [[Datei:Sehnenviereck_Beweis_3.png| 300px]] | ||
|- | |- | ||
| − | | | + | | Beweisen Sie <math>|\beta|</math> + <math>|\delta|</math> = 180°|| Beweisen Sie <math>|\beta|</math> + <math>|\delta|</math> = 180° || Beweisen Sie <math>|\beta|</math> + <math>|\delta|</math> = 180° |
|} | |} | ||
| + | --[[Benutzer:Oz44oz|Oz44oz]] 19:19, 16. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
| + | '''Voraussetzung:''' | ||
| + | |||
| + | |||
| + | '''Behauptung:''' | ||
| + | |||
| + | '''Beweis 1:''' | ||
===Beweis vom Satz 2=== | ===Beweis vom Satz 2=== | ||
| Zeile 52: | Zeile 111: | ||
!Beweis 1!!Beweis 2 | !Beweis 1!!Beweis 2 | ||
|- | |- | ||
| − | | [[Datei:Sehnenviereck_Beweis_Umkehrung_1.png| 300px]] || [[Datei:Sehnenviereck_Beweis_Umkehrung_2.png| 300px | + | | [[Datei:Sehnenviereck_Beweis_Umkehrung_1.png| 300px]] || [[Datei:Sehnenviereck_Beweis_Umkehrung_2.png| 300px]] |
|- | |- | ||
| − | | | + | |Annahme: <math>D</math> liegt .. || Annahme: <math>D</math> liegt .. |
|} | |} | ||
--[[Benutzer:Oz44oz|Oz44oz]] 19:15, 16. Jul. 2012 (CEST) | --[[Benutzer:Oz44oz|Oz44oz]] 19:15, 16. Jul. 2012 (CEST) | ||
| + | |||
| + | '''Voraussetzung:''' | ||
| + | |||
| + | |||
| + | '''Behauptung:''' | ||
| + | |||
| + | |||
| + | '''Annahme:''' | ||
| + | |||
| + | '''Beweis 1:''' | ||
| + | |||
| + | ===Funktionale Betrachtung=== | ||
| + | |||
| + | <ggb_applet width="1008" height="411" version="4.0" ggbBase64="UEsDBBQACAAIAOm18EAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACADptfBAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1dWXPbVpZ+Tv8KFEeVlw7huy+JnJQsx7Zsy3ZsJ+lKpcoFkRAFi1sIypZc/TLV3dXdP6Cf5y9MnK33rpp5d/+lORcXoAhiIcFNFCeJbZDAJZbznf2ec7H7yXmn7bzyB2HQ696sYRfVHL/b6DWDbutm7Wx4XFe1Tz7+xW7L77X8o4HnHPcGHW94s8bMyKB5syYJRZx7R3WtKa4zpnXda3iN+hFFjOtjX3Jf1hznPAw+7PYeeR0/7HsN/1njxO94D3sNbxhd+GQ47H9448br16/d5FJub9C60Woduedhs+bAbXbDm7X4w4dwutSPXtNoOEEI3/jV4UN7+nrQDYdet+HXHPMIZ8HHv3hv93XQbfZeO6+D5vAEHhgRVnNO/KB1Ag/FBTzUDTOqDxTp+41h8MoP4bdjX6OHHnb6tWiY1zXH37OfnPboeWpOM3gVNP3BzRpyMcWKck0lrzm9QeB3h/EoHF/tRnKe3VeB/9qe0HyKrgX3N+z12keeOZfz6187BBHkfGA22G4IbISwh5Ddh6jdELthdsPtGGZ/zuxQZscwO4bRmvMqCIOjtn+zduy1QyBe0D0eAHCj7+Hwou1H9xPvuHxu/AE8Uxi8gcEUATEttQ2d0Qfmr4C/DMVUHntIPHbV4eCs4kWTS8IV1OzXJAs9KR1dlPLsNQkveE5RclH74DM9KB+jLVwq+hP9zVyRlj3m5BXt98UuKNhaHnH3RiIru7F4OOGJGRuzz9DvhEZgqHa4NnyPHQ7CISSwOXewho0kDoiDg7nDOHzFyhFmKx0q4QBzqKMcMw5TJ5IOruAfJqOTCYfDycxeCULpYLgQczh1cCRUzAFRciLBBCElFEZw7nD4kbk8JuYUVDhMwDeqHAb3aGRSYhhI4YfwHS5PHIodan6MpUOEI8z5MDOyLpS5dTglcQRyBDYnBLEGkbbiDOOVQ83TiJhcQbd/NkyRqNFpJh+HvX7yEQaDPrrUd1Y/pdThe7tt78hvg4l4ZoB0nFde2whEdJ3jXnfoJBgqu6818PonQSN85g+H8KvQeem98h56Q//8DowOEzaIxjZ63fDJoDfc77XPOt3QcRq9Nhrdcq+Nxz6TEQPBFzp2gI0f4GMHxNhnmXvdHhxxzkIfrt8bhMlwr9k8MCMuNQMQ8nG3fXFr4Hun/V6QfozdG5G12fXPGu2gGXjdL4BXzVUMXZxL42PUVWJ8qKLJnfQGzWcXIXCwc/6VP+iBqkLSZRwJKTWWTHMNJvXCHqpLyl2BBfzBSjJEQBuFDc8IHybIlVoTzTiIDZcAh3ORf0zz+OL+qxFI3rl/+bytQTDiFvP5ILzVazdHhyMK7Hv94dkg8hxAOw7MY+11W20/4pJI34JZbpwe9c6fxZrTnuv5RR++IXsDR62I8g4oB8LhWVrx9shuozHmzkajUDQGRSNQwm9Bc3QcaxKNiLZHdhuNAga2txY/KU6eEqPkMkEYqTRUiwUnUVeG/Y2RP+sGw4fJl2HQOI0fFdsfPDrrHPkjJkqfEy/rnLs3Jrhs99QfdP12zNSA5VnvLLQyOsbvTb8RdOCrPRCTxDNwfQ43YPc2/dbAT268HXlllmDRUTTOrpnd0anuDHqdg+6r58ALEzeweyO5y92wMQj6huWcI7ADp/4lVzWD0AMz0hz/nZFCePSGMRdAnqEhDcjn2fCkN4j8LlArsDXC1/Y74Gs5w4i9Ig4dkfkwct8MPZ3e0UvQbCPbZ49fAgaHc1ktYkqv3T/xjIsXP3Tbu/AHKTJE53t8fBz6Q+ccpNXw/AU4dWzs8GGv6ad0qNcFaKIHBCXQj1xIAL/v+5Zv7APBhz5cLxK3lB4DOEJzLezy6Fp1ZXz1N9a7t96toYWRwdRV7d4sviDV5laifTuHOzHPWeJmyNw96/iDoDEi5CAiNPz2LD7r6CZSxE8LwdjjFJEfjREflxL/krrxuLBtHHOnE4C7UQcSdTwglgHzKASbM4TYBJi+exmbWMa41NmGmufGvzUfLoxzYj4cB+djnAvMGLwB4fNSvHSpcYZgDk/B5w8jtTiMFWD04V7QbPrd0d3OxAsojxfGQWr0Oh2v23S6kRe2Hwwabb926RZ4yIiE42EDmKX72TA5cGpPFp8igzgI5BjepwsLFppDrIzPaTidqTKxyiU/Kyc/GGe/+wqeA5wBiGJRHCNfIHt7zptkzznQrm5ZAse73uAxdgcQB8G5s5eM30tG7YEXI7hr7PYejc+6x4yqMPK7B96LSs7hf9O19x9ak2B8suAYqJ8jqKdTBNUQY4SKl0VtIYksx+0SGLQoj4/ru0QecazuLm9jDrGbJLV/3m8HjWBYgahHm0XUeUiKY5KiVZA06OSTNK2rnkR2O62qTjM66la5jkob/1tXoqMwiUhJ8kFLoidjReyey7u4xIO4VBFCtOJYS0mpSAw8k0hhpTlTSmC8NGt/K6NE0uA8NPyexuaWNSNeBqJmOUQp0WleregU65QMpdcsDQfdITj/QJCMRERUb2YF4wW2h/YqSQj8agoC+UJiDHHLbo7sZnEMVs30xeo8TZS9K1EbdWp9G1qqN8Y5VmApJcJMIUKEYHjFOmJvio6YTYHvV2HP/TUiUV1FYyykZlpLAeRm0pJfugQTJQUWnCOCsVwa/fen0P+Z3zL789X0XgYIvxyIMD5bQmp/0zQ1uM1SMMa1RBR4XUisI1LXMXM1A3FQEnGqsRZyNco7ombbOFUjZQ1gZRMwp77fN5mvx93nA68bmom1NFcVQxpl1fIB3YcNycP13XflwEb5mhFqMHoibocIBRGBpEKgRpBWbGoUny+FHEfIm00mi0JLwb/UiRbppcd63qBxKYI8caPb7d7rp/5x2z+PyJ7B0e/A3Zu87tNRwjMzJi2xX7c8wGARsd3PwHtcTWyPp2jQdUktSCvhoC2JVJoqqnWUo44iaSI4o0xxRiKTpUUcgUimCFdEaNjFyYo8sDUIcT7Ae0UAt6oB3NoUvVyEMHbBRCLCFAMYYSe1BpGCm8KRMZSUM4T09VXSpfgeZvA9qYbvycbgi9KOJdKExzkDlXLbubXD0phnJCQgj5mEg1sG8K0igINqAAcbD3C9AOG6cCnHMBDEncGvCLtGEJeFHbdfkKuaNoqDQF7m8syQ8JthzgiCRgl2VWDATRElkvAFohokKYgsJxSRpUUvt6dGj+2LVq+br0UNIJG7eysjbV8EcMbGaZz88KIsCAw8ij7Qm7XmCzwt4rQXTqAdnXBeVq4uypjTcV95nimvKQmOSaXjTc/7VL/XRVwHcAIk4xBzUEFR5ANGloUhcB44Bh8BYmnBjEy9MTWJREgusEIEdA++VgFeOS5HG4VLASxmt4mwuUaMEw4H45QpUYoJwrEEFYKy1RfXFpXmRqHy/ykBku96WXOQGz01qjlfjQ0Jj+GnWihEEZZaaoiGJEumIzRDRIP8YS4RViz2rQU4aAq8NIY4/KtKAJ42773RAGfTWy+rAfxyQwAuUKX1IhNXr2LjriPEsWeXdeja1QBubwjAlxOIuUq5kk6+jniORDYbEHeqIdrZlIDYhL1UE6EgQpJCg3pOvFIpCWWSKgiSwNmxOpm4DHBVUhCNFLhGmJcgfB2t7mGRze1Ww7e7KfiC8pVKYmLSF0xLpUgSdojJmT3AV0BkzMHhlZQSAFfr7YQ3q5D71eDtbwq8FfOV1zmZVQHfrEf1TTV8v9l0fAvTlduTkc6bFz6cSJVl9fS776blwibnhuO4d2x2GLlg4pjiICYClCPCYu6kF1FjHBF9i3kCV0iXWsRp/hRxGcC0whSxmHWKOJ3yNPSbkvXMA3Isuo2AzDpU796+oJWANOOzQGpGlZmCM2LCEV8/kJdIleWKVoDUXJK1X5SCfvf9C1IJju/j+YUUHEoSQSDap4hRItj0sosCOJJmqklNuyVg7CduSrFsVAPj7QxgkHWDcaniGImTfXQjVRxQbw4Vd5gCMaeG6W1FS/U2z1IxjQg2Xr3QEJRRPbepsq4LRvOjSGx1YEHbyppBnKvebK9Q4H6qhNRPG4jTNVF9hykkbr8gWSy+rYTFt1kspEZIKcaRBN0n0dyKLzUVjti2QTE5L50jFt9VtEPf5dkhiFI4k1gjKSDMkQtKRnU4xlxtEUdXTGyCDsvxtbOGqKzG49O1VnjM07Q1tYbDTJtjLBSPklJUURzXoFOXaK0IB56RwDxk/hr0Wal5Z74uko0ip4wz+GSBLuqKrbifWjVyJ6M9wnLVkW7FDa82IzNX/mQt3bZ1xVwuiDK1qNxUmsqJ1ts8ATKNuFkBys36jLflVuuLCTOI3y1HPC1ud+cTN0xsNBJt569RY3Gv6Or1GyApCGNUwh1jQZNJU+yaKRmCpJSaMBlPmS5XXmdD7V4V1O7NW0SyAGwrAUa5IDEaM0SY4IgLtUqzM0tu+67Vo/cy+AzL8ZnMbQ+XoEnH3atpnS4Zb3e8YIAxaWoDsFTgAUqbBsDaFUhRoC/IRBQvRTTmxKUU3ENm0haYsrJ6ELTRme2nvaE3nDSTMbx1CFgib/vTrPZ83+v3wo8q6dD4J/O4gUuVyDGFJ13MuKKaSqakBoBt1sA1tXaEcBME6KSgYKlilU/2mEIx8X+aQvy5IdhAIIgLIicZpkgoIZmMp/6Fy7gpBFBSKEpIPPO/PijSgLxNip2nQLIgMEXwrNrjKO0URwxzCnaGYK1BOmzRvKuFcfUAM3D1EGjBq0BnEiNShNFBFUQONor+0tWMgT8tBMIqaX02NYyIUnAHuOYKXIHldOrPQP+DhNrfl1C7uhQcbCDnS5dQTsHx5RohEk222aZ/gjGiHGNQWYix+fs2qpJ+kt3pFADmhmE2MNbhQqcriCRGnBKKhTTVIyqZrQFLTrhSkmrNpFqf0T7I00LfFVuKg8UsRd7PN0le6tolRGMkmYaNUjE+2gWPmgqKianyWmCRhkXQmcSoUHfdr4LI/SvNDXAbp7D82cqczp/JEJ/mhvgUrcKYFwST47hkwWhMm5rM9BjM3T2y9JIpY7e56auXRFKwFSr2mxSN3CksIa6HQNLmUwjEmhCBQjgJqg08qtIug82ul8oHOs6+ZsKX9DIpVeH2NwduUHMS3DEkwE8W4DEnSwRhlyGBOFdMA9yCKhE3DkkXBFEgxDElim9fDWSho54V8+OquB9vDu5g84SWBkqqkdKSJ/k5cB0J4YgY2JkcWT1NwThqiKUkMo7MloEei/lBBuJWVYhbmwOxAVMj8DipwmAdSVy6DshzYUIvUOVk1L9NBGAsKeh9bYrXpd621oSDclk+qQr0yQYBzVxA09SiYVDIimOWRHycSSQoAaeJ8njRnDqNcoVm7SaQaEKw3lZhLrXZQVW8g83BW7uKEVDcEMSDDCuN49wKZwZs0N5CwL9o1FUmNBMIfGezWoPm2ybYeXAXgP6yKugvNwd0bgpOOZXMCC24XTRZjMO8BQLQpuCr8SShWcfKZWCnNZKUghuPtlTG72cgPq0K8enmQFyfmNCLpu4uYh8dgaSDCGMzeTpS5KYEjxEBfAEscX27zfLK5ybsdZT2yPpn734sR3uigO7HuWrqZ2kWLqriNmvUzZgYiRO1BVXcZbWO+MqLHQ9SOBVMLaWR+3Ml5P48FTm5fORmXYMSWwss9TVEriTezWKZRfEvlVD8y7TKbkbzeoxm79aPFlOZgFGIGWGk1qaOmv6uLYx5AGah+2sl6P46Fbp5VWcJcnpG5OKqzGuIW2G2PzF55eL3j0oY/mNqqyadE8PiBr+pKF5LpPIwyqLzz0ro/HNa/2XyioHlolOuHa8lOjkYZSOFd/+qhM6/sotgMw1BuMJYMIxQ0l+80DIz6cLA0WzKNPUHjse19Rzvz2Ss/v2fVcCC0TlgUbN+FheMCpCmpYMlZ8XKVsKQzTNWZTPGD7ageYMni+LRJXVvlBHs4RYQTC+bYJOZnU7QyGt5eWBVwsOMFuhPS+5ETS99bzC21MxVp3c2t/WFR+9tT79nLmpwsu0taCNSQ/npv0IOaVdN/7XnfbvRCtaqQXEpdyxsZFUvWFsDbIdBs5/THVOI26Ny1NK69dFCEr2E3u9sQ+CKVGRugdiDTHH3oww9H1Qv00t+crV2a9xcE8q5WdlUIMYpsT5uHaSCK2oSf2Z1cqnWVkH8YDyqGKvaLiT+3BBsGBDC5UoioLRQkphSu6RCCDFqyrkRJeBTy3h+eX1IFNSvTsFjQVQ2DBvlRqv7KjNzwQW6xIZLyZFWgkoEoiJX0YWSF82lhOSRBeRBNpr7TaVo7jeLpx7LAFlk0Za6jKuFC17lubR4ztzk8oPvHElKQCsKxH9bCbrfLj7hlg/d4qsm1eOWoPqq8/1rgK4YwCIYf1cJxt9NTRznrQIzU3Pe4iv8xbNvdc42Hcfp1qyg3j9r0x5XsWCPN8heafhPgB/BCCKUjpw6rRQHN4NTDh4GYavwJfKk6HGxzBRJzp8qSc6fpi3Yo6ZOucwAzlzL9fBY/8nNExv/vD+AK5n0VUyE5/75EJgFDtysvf/NWW/40c7XEal3nF86dkd0kjQYQ/hVLX2KclpXjBwrS0IQPvSe+79Kh9Hv7R734JZDfxAcJ/djXiIJVwQ5iAP4ZO5n6A2G0cITjg2ShFkNDcO/EAwRHXsjzBXGY5fAY5hqIlOdMbOmMJ9sQQpTrDPn+9kWEEytOuebl857YrXwZxll26mazuvkpfOu9GUPyVJRojSbpzYsm5evgEm+Ap5d/U57Z94ss26LSMiy1S+E31gITDjFzMSiMlG/Ckv4nyPBkBKKFarfXDLTFJmdMUNXgdR0PlIXV8NdMamFS4HMYNTM+8MEwyNSS2pq26UCZ4pqTquRmi3uUrDFCB1tN4vU5v30mCFwUimnpstgxNVmASGqlEYEYV2R1DxF6pvODhXof/57Z3ZC8yvV7PMTGeUS2bzWiUli2jekxsiskiWT5J3GikE8xDQ2QOCK6gOjSUpjVY3ScIbrSeoiLY2I0IhJJsAjVipZLtvF3GQPtcKCm5fyyHm85KfLWA9smV6feSHoAo4ydpezVF4ZzZ5d7ZT8cgILvj56fbkFgYVcJ4N9tRUEWyOH7S2jDOLKSTamxFYf7e9vCcn4+kh2eytIJtfJZZ9uCcmWzGXTM/vPbE7pqc3s773AmeTSu7cvWHl2KfMGETaZzTcT7UhqQYl5G6DSIm/5/UUyzMt5GcKUYrF05XDcgbXU2covLRrPLBr7eWj8UAmLH1aGxGpfjlQFCVo6cTJfW+1XFogva/ELQnKA+FslIP62MiBW/dKw1UJR+iqErVDqatke/XTuvRMVeWHLxsRaxwz//r0S//59xSo9C9Z1597nW8C7dZJ4JGQN0dXnW0ax1bu9X2wVxdYRwd/dCptimWtdXHZvO2iG1ymZB9tCszXy2f3toBlaJ5892A6ajemz1duAh9tBM7xO3+xwW2i2Rj57tB00Q+vks8fbQbORPluHT/tkO2iG1xkHfLYtNFsjnz3dDpqhZfPZDMuOJQm5z21C7ouYRmP9Er+3Z52xX+L3P6fj5srr30uAuJv0wT7OyY3++w+VwPjDz7n9eVcvTeC4l8DxJA+OP1aC448/z3nNBcb9BIyDBIzP8uYNvp3WbDAxc/BtbDW2ezp4FYA8SgA5TAA5yAPk+4qAfP8zIHMCcpgA8jAB5F7uFH1FQH5YISDbrbIeJoA8SAC5mwfIjxUB+XGFgGy7SX+QQPLcAvJ5Fo6fKsLx08oV1vV0dwv6GlJtDb+s0M5wpd0M420LcUw5Y99CnbgEcUkRw5RpwoSkSb6KmJeqY8aQ5kpES/JU6RAR81JSXFdKYlciJAUyb51nVCTv4JwkZMWWJjkvHeX1pSPBhDIJ6l1JDASVI0JiThUh0qztIHhhK810PbtvteytuHAzq2XfVtKxb7MalgqiqJZCS6o5n7pub7W1g0z7TSU0Fi/YLNWv46kirx+lmKL9O+/e7syod9Ntv7f8137L7zrPAt/ZcW7D39d+ANCc/e9/+YMTr33kNP3QeTDwgxC27/8HRh+dAeBBt5s97FZQ4kvoHV5tT1pKlNCU9j/qIsIUZVwRjDlP2lllejevqNhVCqkvvdDpezDIHwydDmC083XTbw+9HccAsvP1kW8+O5/MDoLadAzG+wLRFGUGEGCpQIKB4qY5cASBZBy0mdKMMc24mF+V7VlVdjtZxmc/J8atFuFmlZmUZgE+Yl6dIQXTU1+fcb21WZ63CMTrhnAgWvfAfG/5vZZ/NPA+/j9QSwcIxyL1ciIYAADS1AAAUEsBAhQAFAAIAAgA6bXwQEXM3l0aAAAAGAAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACADptfBAxyL1ciIYAADS1AAADAAAAAAAAAAAAAAAAABeAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAALoYAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | --[[Benutzer:Oz44oz|Oz44oz]] 22:47, 16. Jul. 2012 (CEST) | ||
| + | |||
| + | |||
| + | <ggb_applet width="1008" height="411" version="4.0" ggbBase64="UEsDBBQACAAIAEu38kAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiu5QIAUEsHCEXM3l0aAAAAGAAAAFBLAwQUAAgACABLt/JAAAAAAAAAAAAAAAAADAAAAGdlb2dlYnJhLnhtbO1dW3Pb1rV+Tn8FRkfTl4Twvl9SuR1ZTmLFlp3ETtrpZMYDkhCFiLeQkCx7+nKm7bT9AX0+f+HEufXemdN39y+dtbEBiiAAkps3UWySKCCBTVzWt9a3LvuCg59dddreZTgYRr3u3T3soz0v7DZ6zajburt3EZ/W1N7Pfvqjg1bYa4X1QeCd9gadIL67x0zLqHl3TxKKOA/qNa0prjGmdS1oBI1anSLG9WkoeSj3PO9qGL3b7T0OOuGwHzTCp42zsBM86jWCOLnwWRz3371z58WLF352Kb83aN1pter+1bC558Ftdod399IP78Lpcj96QZPmBCF85xcnj+zpa1F3GAfdRrjnmUe4iH76o7cOXkTdZu+F9yJqxmfwwIiwPe8sjFpn8FBcwEPdMa36IJF+2Iijy3AIvx37mjx03OnvJc2Crjn+lv3ktUfPs+c1o8uoGQ7u7iEfU6wo11TyPa83iMJunLbC6dXuZOc5uIzCF/aE5lNyLbi/uNdr1wNzLu9Xv/IIIsh7x2yw3RDYCGEPIbsPUbshdsPshts2zP6c2abMtmG2DaN73mU0jOrt8O7eadAegvCi7ukAgBt9H8Yv22FyP+mO6+fG78AzDaNX0JgiEKaVtpEzesf8CfhjKJXy2EPisavGgwvHi2aXhCuo+a9JlnpSOroo5cVrEl7xnGLKRe2Dz/WgfEy2cKnkv+SvcEU67TEnr2i/L3dBwTbyiAd3Mls5SM3DG56Ztqn6xGFnaAyGao9ro/fY42AcQoKacw9r2EjigTl4mHuMw1esPGG20qMSDjCPesoz7TD1EuvgCv7HZHIy4XE4mdkrwSg9DBdiHqceToyKeWBKXmKYYKSEQgvOPQ4/MpfHxJyCCo8J+EaVx+AejU1KDA0p/BC+w+WJR7FHzY+x9IjwhDkfZsbWhTK3DqcknkCewOaEYNZg0tacob3yqHkakYor6vYv4pyIGp1m9jHu9bOP0Bj46JrvLD/l6PCtg3ZQD9vgIp4aID3vMmgbg0iuc9rrxl6GobL7WoOgfxY1hk/DOIZfDb0vgsvgURCHV+9D62GmBknbRq87/GjQi4967YtOd+h5jV4bjW6518Zjn8lIgeALHTvAxg/wsQNi7LMsvW4PjngXwxCu3xsMs+ZBs3lsWlwzAwjySbf98t4gDM77vSj/GAd3Em9zEF402lEzCrqfga6aqxi5eNfOx9BV5nyootmd9AbNpy+HoMHe1S/DQQ+crPYpZkQSQZQUWoOVvLRHagppXwuOFadIcKrA+oaNoJ0QE/LB7xDCGFJCEwKq8LL8mJDSXju8HGEUXIXXj9saRCNlMZ+Ph/d67ebocCKAo6AfXwySwAHIcWCe6rDbaoeJkiR0C165cV7vXT1NidOe69nLPnxD9gbqrUTwHnAD4UCsrXRbt9ukjbmzUSuUtEFJC5SpW9QcHceaJC2Sbd1uk1agv/bW0ifF2VNilF0mGiaMhvZSu8nYymi/8fEX3Sh+lH2Jo8Z5+qjY/uDxRacejnQof068qnMe3JlQsoPzcNAN26lOA5YXvYuhNdExdW+GjagDX+2BVCSBgetTuAG7txm2BmF24+0kKLMCS46icW0t7E5O9f6g1znuXj4DXZi4gYM72V0eDBuDqG9UzquDGzgPr7WqGQ0D8CLN8d8ZI4RHbxhvAeKJjWjAPC/is94gCbuAVWBrbK8ddiDU8uJEvRINHYn5JInejDy9Xv0LILaR67PHrwGDw6Wqlihl0O6fBSbCSx+6HbwMBzkxJOd7cno6DGPvCqzV6PxLiOnY2OGTXjPMUWjQBWiSBwQO6CcRJIDfD0OrN/aB4EMfrpeYW47GAI6huRb2eXKtmjKh+isb3Nvg1sjC2GDuqnZvEV+wanMryb79k/1U56xwC2LuXnTCQdQYCXKQCBp+e5GedXQTOeHnjWDscarEj8aEj6cK/1q6abth28TlXieCaKMGIuoEICwDZn0ILieG1ASUvnudmljFuKZsI80rE96aDy9NbGI+nEZXY5oLyhi9AuMLcrp0zTgxeMNzCPmHCS3GKQEmHx5EzWbYHd3tXLqAynRhHKRGr9MJuk2vmwRhR9Gg0Q73rqOCABmT8AJsALNyv4izA+f2ZOkpCoiDQY7hfb60YaEFzMqEnEbTmZpmVqXiZ9PFD7457F7Cc0AsAEksSlPkl8jenvcq23MFsqtZlcDprld4TN0BxEF05R1m7Q+zVocQxAjuE9DAQ5qe9ZAZqjD2ewjBi8rOEX7Ztfc/tC7BhGTRKUi/xFDPZxiqEcYIlaCI2lIWOR23a2DQsjo+zneZPeKU7q5vYwGzmxR1eNVvR40odhBqfbuEuohIcSpStA6RRp1ykea56qPEb+ep6rzAUfemc1Te+d+7IeePSSJMUg5bhe9fxPMTnypCiFYcaykpFVkcwCRSWGnOlBIYrywouFfgmjyGj4xZ5CG8Z71NUECyOR3JnIU1b9bCqqmnIOkNG81xN4YcAQRSMJxE6s2i/TzH9tChkyHBr2YgUG5Lxl+37KZuN8tjsG6lr2b9vFAOF2KXhSUylltQGwXRqfwyrrQCSykRZgoRIgTDa6aJwxk0MR/VH7lo6NFGqX5NZI4oUZJKJjWVmGJpYZI+5lQhThhWBFAUK8PpaAZOT8OW2V/O6IcFwMLpgA3Ts2WQhNtG6hCIS8EY1xJRsAkhsU5EXcPM1wzMRknEqcZayPXwfCLNtlGREa8DWMWSznkY9k0t7Un32SDoDk1PnW0zViqqgDSp05UDegQbUobrm6+nA5tUgEaoQeuJSgDkPIgIJBUCukFasZl1gXJr5ThB3mwK9kqngn/NnRbplWePwaBxbYI8C8zb7d6LT8LTdniViL2AY9iBuzeF4k9GJdRCm7zFft4KAINlzPaoAO+pm9mezmDaTVktWCtQJMKGKhHXSBNtrRiUgWnKBUYM/jXdnjTNaTCoIBi3ZMIYuFT81ppxOcSHVRC33CBubQszV2GMfYY5RpRrrTFjplMj8YnEVwgJrcBhghdldEcBPikAfOYG8NnWAIzyMSggzNNChMoF+dy6Ymk8NBKSMIUZGPCaEq4bA/heFcCRG8DR1gNcq0C4JnzKMTSkijL4FWG3COJpGcr95+Sm+qKoZU1GSzFbYQoDLtaMLyIYY0qkUEKnYAsfchpCKAd+JphoubIc5v7MXLP9stXrlhOpwSQJeu8VDO6zCM7YOE+rJUFSNoGG9eQDvbvXfI5n5af2whm6oxMuqs3u1gxucDxiXqQrbUZFZJJ3gtmFIvd7XSZ8gNCAaxMNKAEug5CMe5iWkGwjKoSGj9LWPmoUQkTwL5JhoSW04LeXfCaRqW8VMhXAEJ8ICNKlBB/PNPxnaYL7WBAphVAUfAa6TU5/OijNrQLlP6kOUh5+WX9QmkI13AKwxpZkyZAMC8QVFgIrxAFJliZQGhNGsQACRJoxNkqgtImsBZOEMgREuHhJZLsBLla5vnAD+IstAbiCSSs8nJODu40Ap4FdMZ5ru8Hb3hJ4rzscSynZiZFvI54jgy2mxB03RDvbkhJjnyCwWUBNa4h1EE0BplJzLhVkyUC+2NYstU+IgByZSc0wZFZ6xxzuSZW77bqB290WcE1ZgwlwsxKcrgTk0u5p5PNC594r0zUCu4mClBhJLjjZUXyLdNx3w7e/Lfg61itvczHLAd9iNPWlG75fbju+leXK3alIl3UNn0zUyYpE/ebrWYWwye7hNOcd6yBOyJHCPwxhTSGamd1DXJUWEzWmEcm3VCewQ7nUIk7Le4mnAUwdeonFvL3E+Xqnkd+MkmcZkGOZbQJkMZx68/o5dQLStJ8AEvtYG74TmirOMc464DYJ5DVShek/60VqIcs6qqo/v/nmOXGC45u0fyFnVyayUJwIDvEjUowsCkc2Q2uSaXcEjKMsTKm2DTcwXs8BxqaxuGY4lpbBcXmH0E0zHAhvAYY7yWFYMorptaOjel3mqJhGBEMkIISGvIxqsSiKNnLBaHEUiR0fWDEVZsMgLjTi7LDS3r53Qur7LcTpljDfSQ6J+89JEYuvnLD4qhgTUKGkFBorirEWaOGYINcTjtiuQTHZJ11iFl87uqGvy9wQF1QjiNK0gqyUSrVpOMYibZEmV0xsA4eVhNpFRzRtiMd7NzQIff6JYDNHcCQj7rBQnHFIckFBslHo1CdaK8KF5lJiTRYfwTGvNN9fbMrJVolTpuV7ssTMbMfpve9ZGnm/wB7D6dSRn947vNmCzELlk43M4K0pBgxKlAZ/xqXAVE5M5y0zIDO5t2hApUWf8am+bjNohgXEP5iOeN7cPljM3DCx2UiyXXyIGkvnn66f3wBJQRijEu4YCxMZpmMeIDVjBEkpNWHSPMXK7XU+1B64oPZg0fEjS8C2FmCUDxajMUOECY64UOt0O/OUtj+wPPqggE88HZ/J0na8AiYdD69mzXUpRLvjPY+MSYaYxlIxiaUtA2DtC6QoyBdsIsmXbNcU8Sll0gwFEQTTUZpZxsxoqwvbn/TiIJ50kym8NUhYkmj7vSJ7/jjo94Y/ceLQ9CeLhIErtchcQKc4wkpIgyzwmrABnQB7o4gzLDDjSlKyBsMqF3wqo1T8388Q/8IgbB8UxAerAwtEWCKgNG77GbgvqKSamixZJEtsbhiJPB6vs5HOMxBZEpcqdNYdckyBByxCgE1IjjTQnlIijdwFEQJiOQ6kSfkyQ9eXgWcSJFIF0rELJMdbBYDywQywYBwrQqlmaT8c9xFRjFOBtRnAmHa8bgCA40zc30wRt7sdHG+h7jMfUSaYBglrpKlKoy8Ils3YUQiVsZm9IdjGlP94UuHpDAQWxmE+NDYRRo85bemDa5ZICARpJGEaj/AwyaVGwFJw1HTobRaPPCpfV/uK4+V8RdnPt8leahjCcCJYMpuJCpGuyAG4ETNDQSKEuNJMLb5WwzL4TKJUyV4fumDy4Y0WCDiZNoetBKCJPF/p0jw/G2i5kYxyHJciGI1Z/ZOFOQYLzx5Z+bApDaEtUVIrblaJF9djHk3uQTEhmkrCsyHLpj+IEEUZJ5LoXRsTlxZgC/lLfq0UV7DD7QG7pnwDJ9YIYjXKIFazpuljriFOMDmOMTgLN/ERMvs1NWbH6M7BXRmmFy381BX00+0Bnfsa/J2iyNRGTXE7c3hgy8a+hVAYSazSmWLKB/2ASD5Zcwpixx0DPbXx4wLELVeIW9sDMfYlUYKAX6QKAhhqPa72JWIKUoOkdiSlNWvKfKLNAHdGMXhSOa06eBsBPp5uyWeuMJ9tD8xA30RhyKg5lmChaRUY0mzIACnlDANRG4tNDJkonyOOOTZrzgusuNgxoDNLnuqtI1e4o+2BW/kIYyWYkFpTyCR5BrdkFLIXbKZ6KpENZ1c+OG9tcn1BCNm19XPKwK6A/AtXyL/YHsipr5WiCmyWKQy0rVJnrUEVmMTGgwO7cyRTG2c+WDgD2zZTlDSRO2rjHxZAPncF+Xx7QK5N9OZpPkJZArTc9DBg878UZfDYCEyeEUE4gE9ur8cuGzw34a+TekcxOnvz3XS4J4bPfTdzDHdaHnCeJ1w1hhv5oyn3M4f/2hptxRjuaQE3vvGhjsc5nCr6lfLI/ckJuT/dBHLzrkGJbTVX6luI3JRst4hlEcU/O6H451njulnZWOL55+kni6hMoCjEnCimVY/RhL9bi2IZfkXk/uKE3F9uAjk9J3LpkMxbiFtllT/zeNOt7+9OGP595jTNsqHj82BYPblvJoq3EqkyjIro/MMJnX/MnHsp14HOdHa8leiUYFTMFN780wmdfxbXwDajF5VZyhYsh7BFTad6VKBQc9Kf1Lc3cPxwLmf17/92AQtaT4DFfLOqMDKrzZlxc2T1YMl5sbI5Hdk+ZzWtp/jhDszc4NlieHRFUzemCezRDghMr1pgk5WdTtQom+/y0FLCowIL9GcVd5IZL/1gMLbMzE2Xd7Z33gtP3gOff3FdMrvJzm1BW1EZKi//VWpI27X81170PUhrWKcGpZ3uKFu5cRkVulnYTqJmv2RqTCVuj6ejlufWx0tZ9AomfhdnA66JIksHhj0sDOx+XJDnQ/cBetlPbtZvjbtrQjlniGgzZJJm7wIBq+CKCoI0IkRKtZq3gs0j9ooB25XCXxiCLQNC+ExJYl7Cgcwqhopnw+6QEIonvYpCILFpICoGrs6AY0lQtgwa6XNqVuEn3KCQvqDaICMh19GMcmxW5ifrGLNalsvlTOSxxeNhMZf7tVMu9+uZhceydXfmnqW/zHotNZmOqq94L+jKsjlzk6tPvUsMKQOtKg3/jRN0v5nZZzOzZlwO3fILJtVYNmpizdX+DUBXDWAVjL91gvG3s8rGejEUV7G0X9rzVhste721MM72ZRWD/Ise7YmL/3qyNd5KQSDBCSIK3FOytmbmriB8AIWSIGMlOJHrGL9fZkRPqk2mynD+6GQ4f5y1VI8qW8TKdYGZhRbq4Sn9ye0zm/CqP4ArmdpVKoRn4VUM4T8cuLv34y8vevFP9j9PRL3vve3ZHclJ8mDE8Ku9/Cmmy9oxbXS2hGj4KHgW/iKfQ791cNqDWx6Gg+g0ux/zAkm4IoRtafaevS8oDgZxsuSEZzMkYdZBM/1DkAkRnQYjzBcSSSU1kphqItW4Oc1bv/xoB+qXYpMF3493QGBq3QXfslreR5aFPy6Qbce1ltcpq+Xd6DseskWixNRSntqyUl45AZNyAp6ffme9LG+eLrdlLGTV9AvhjHkJD+EUM5OKyox+FZbwL0cCMhyhWCX9loqZ5sTsjTk6B1HTxURdPRLuhkUtfApiBqemmCCC4ZGoJUUAgDSvJaSaUzdRs+VDCracoJPtdola+mYGgZmrTjmliLGRVpulg6hSGhGT9bmJmudEfdfbpwL93//uzy9ofqPMvriQUamQzesKmSRcaSw1RmZ9rFEypLFiSnGmsQECO9IHRpOSxspN0nCG2ynqKpZGRGjEpJkug5TKFso2U1uFWYkMC26W6ZGLRMmfrGIlsFVGfeY1oEsEythfzVJF02T29Gb741eTWPDNyevnO5BYyE0q2C93QmAb1LDDVYyBuHGRjZHY+rP9ox0RGd+cyO7vhMjkJrXsvR0R2Yq1bHZl/6mtKX1iK/uHz3GhuPTm9XM2vbpUeHcIK47P5xJJLSiB0JIpLWZW82/kjRQzRorlhw2nHbIr7az8uUXjqUXjqAyNb52w+HZtSKz3rUguSNCpHSeLTan9pQXi53vpq0FKgPirExB/XRsQ635b2HqhmPoShJ0gdbXqiH629r6fDPHCVo2J9Y4F/f2bk/7+bc2UXgTrtmvvsx3Q3RrJIhKygezq0x2T2PrD3s92SmKbyOA/2AmfYpVrU1r2YDdkhjdpmce7IrMN6tmHuyEztEk9e7gbMhvjs/X7gEe7ITO8ydjsZFdktkE9e7wbMkOb1LMnuyGzEZ9tIqb9aDdkhjeZB3y8KzLboJ59shsyQ6vWsznWHMsKcp/agtxnqYzG5kv8zp51zvkSv/uhHLdQXf9BBsQH2SzYJyW10X//3gmM3/9Q21905dIMjgcZHB+VwfEHJzj+8EOf10JgfJiBcZyB8XFZv8FXsyYbTPQcfJV6jd3uDl4HII8zQE4yQI7LAPnGEZBvfgBkQUBOMkAeZYA8KO2idwTk2zUCstuU9SgD5GEGyAdlgHznCMh3awRk1136wwySZxaQT4twfO8Ix/drJ6zbGe5WzGvITWt422E6w43OZhiftpDmlHPOW6gRnyAuKWKYMk2YkDSrVxHzOnWznKXmSsAhtxkiYlFJitsqSexLhKRA5n3zjAqkygXpOKVJLipHeXvlaF6NySTQu5IYBCpHgsScKkKkkPDHK6fSzObZI8uy99KBm0WWfe3Esa+LDEsx5ggQJ8y8c3XmOrBuSweZ6TdOaCw/YHMqv46XioJ+UmJK9u+/eb0/J+/mp/2+iAZNb9+7D3/18EXYit/x6u0wqsfe/uf1MA72vdNwGDuw8womBa93slnORtCMeX3ER5hqbV4TS4BUuH1rZk34RDGJKKOSYbOSt+Ocvvyc4P033+x70dDc4dnAG/aj+BVIvx2exp9fhoPYS4DwPh9ErbN0z9ve+OFm2J44vu95vdPTsFsPBt45wNkF4cFj//i/MPqJ+/xBh8nHjV63GdnKJzR/kra+f5N4j08unAU38zkhnEjw0ELx7PV6ADc3qyMhIEMmuGao2kPnRFnv9dph0L2eMTHJXmOS25DFXC8YIzCa9o6TOVVZ5TX5/r7XjoBFvODiX/8TDs6Cdt27hF/snzsonNp2CnFRKeKLZEVFybQGJ8uFzHRKgiZJrjBmHNRLcEcOyQfQlsKt7KNud1HR45uNrlcue4WRgsAApCuBqzP6lhAoMg37iFBA31I7ip5V0Hd80emfvrNC7m4N/vWdsaMlyNthQYNy8r64LWgb8lYIkJWCao5whjVWilMqMeIcqeTliosGs4c2mL2fLeR2VFLldKtxFsNZpAWhikMoSjEoLNnteHb2aPVJH3qxVT6UWDbHrHy1wnkJhVdyeXBx6sjgt2phjVk2TX1EGJIQaguiBc7WjE7WgKBCKCkYhcyPOBK4mFgoZmV8DbF24yxbosP7mQNsDsWYcp6+vC2YMvC+VBGMiBIaCTGGKSIcAm/NNcFzLnI3SQ+X20QP2Vtdybz0AH6jO4Q7Sxb9Mt9bYa8V1gfBT/8fUEsHCOmNR3xzGQAAHOAAAFBLAQIUABQACAAIAEu38kBFzN5dGgAAABgAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgAS7fyQOmNR3xzGQAAHOAAAAwAAAAAAAAAAAAAAAAAXgAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAAALGgAAAAA=" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | --[[Benutzer:Oz44oz|Oz44oz]] 22:45, 17. Jul. 2012 (CEST) | ||
Aktuelle Version vom 18. Juli 2012, 21:59 Uhr
Inhaltsverzeichnis |
Definitionen
Kreissehne
1. Es sei  ein Kreis. Eine Sehne des Kreises ist jede Strecke, deren Anfangs- und Endpunkte Element des Kreises
ein Kreis. Eine Sehne des Kreises ist jede Strecke, deren Anfangs- und Endpunkte Element des Kreises  sind.
sind.
2. ..........
Durchmesser
1. Es sei  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner seien
. Ferner seien  und
und  zwei Punkte des Kreises
zwei Punkte des Kreises  . Ein Durchmesser ist die Strecke
. Ein Durchmesser ist die Strecke  , für die gilt
, für die gilt 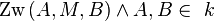 .
.
Radius
1. Es sei  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Jede Strecke, die den Anfangspunkt in
. Jede Strecke, die den Anfangspunkt in  und den Endpunkt in einem beliebigen Punkt des Kreises
und den Endpunkt in einem beliebigen Punkt des Kreises  hat, nennt man Radius.
hat, nennt man Radius.
Erarbeitung des Begriffs Sehnenviereck
Sehnenviereck
Ein Viereck, dessen Seiten Sehnen ein und desselben Kreises  sind, heißt Sehnenviereck.
sind, heißt Sehnenviereck.
Sätze
Satzfindung
sehr speziell: Quadrate
Jedes Quadrat hat einen Umkreis und ist somit ein Sehnenviereck.
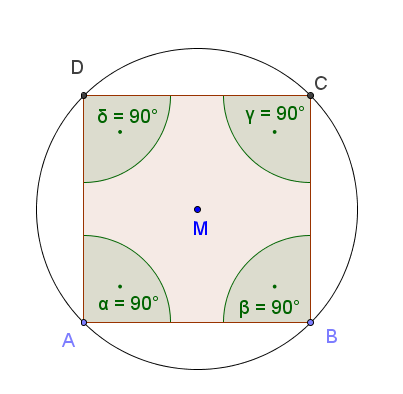
weniger speziell, aber immer noch ziemlich speziell: Rechtecke
Jedes Rechteck ist ein Sehnenviereck.
noch allgemeiner, aber immer noch ziemlich speziell: gleichschenklige Trapeze
Jedes gleichschenklige Trapez ist ein Sehnenviereck.
allgemeines Sehnenviereck
Ausgangslage: 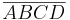 ist ein gleichschenkliges Trapez.
ist ein gleichschenkliges Trapez.
Arbeitsauftrag: Bewegen Sie den Punkt  auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von
auf dem Kreis. Beobachten Sie, wie sich der rote und der blaue Winkel verändern. Was vermuten Sie bezüglich der Größe von 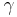 ? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?
? Was vermuten Sie hinsichtlich der Größen der gegenüberliegenden Winkel im Sehnenviereck?
Der Satz über die gegenüberliegenden Winkel im Sehnenviereck
Satz 1
In jedem Sehnenviereck sind die gegenüberliegenden Winkel supplementär.
--Oz44oz 20:32, 18. Jul. 2012 (CEST)Satz 2 : Die Umkehrung vom Satz 1
Wenn in einem Viereck die gegenüberliegenden Winkel supplementär sind, dann ist das Viereck ein Sehnenviereck.
Kriterium
Ein Viereck ist .........
Beweise
wir wissen
--Oz44oz 22:55, 17. Jul. 2012 (CEST)
zu zeigen:
--Oz44oz 23:03, 17. Jul. 2012 (CEST)
Beweis vom Satz 1
| Beweis 1 | Beweis 2 | Beweis 3 |
|---|---|---|
 |
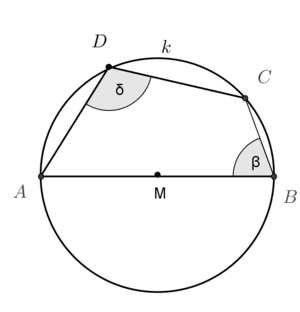 |

|
Beweisen Sie 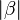 + +  = 180° = 180° |
Beweisen Sie 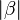 + +  = 180° = 180° |
Beweisen Sie 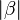 + +  = 180° = 180°
|
--Oz44oz 19:19, 16. Jul. 2012 (CEST)
Voraussetzung:
Behauptung:
Beweis 1:
Beweis vom Satz 2
| Beweis 1 | Beweis 2 |
|---|---|
 |

|
Annahme:  liegt .. liegt .. |
Annahme:  liegt .. liegt ..
|
--Oz44oz 19:15, 16. Jul. 2012 (CEST)
Voraussetzung:
Behauptung:
Annahme:
Beweis 1:
Funktionale Betrachtung
--Oz44oz 22:47, 16. Jul. 2012 (CEST)
--Oz44oz 22:45, 17. Jul. 2012 (CEST)


