Lösung von Aufgabe 4.2 P (WS 12 13): Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definier…“) |
|||
| (7 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert. | + | '''a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert.''' <br /> |
| − | + | ||
| + | Ein gleichseitiges Dreieck ist ein Dreieck, bei dem alle Seiten gleich lang sind.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:45, 22. Nov. 2012 (CET) | ||
| + | Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:45, 22. Nov. 2012 (CET) | ||
| + | Ein gleichschenkliges Dreieck ist ein Dreieck mit einer Symmetrieachse. <br /><br /> | ||
| + | Robzimmi, kannst du bitte das nächste Mal deine Signatur anhängen, danke! Ansonsten eine super Idee, Robzimmi!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:30, 27. Nov. 2012 (CET) | ||
| + | Ein Gleichseitige Dreieck ist ein Dreieck mit drei Symmetrieachsen. --Würmli 16:52, 3. Feb. 2013 (CET)<br /> | ||
| + | *Super! (Ich würde noch 'verschiedene' Symmetrieachsen einfügen)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:08, 4. Feb. 2013 (CET)<br /> | ||
| + | '''b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.'''<br /> | ||
| + | <math>\left( A\Rightarrow B\right) \Leftrightarrow \left(\neg B\Rightarrow \neg A\right) </math> | ||
| + | Wenn ein Dreieck also nicht gleichschenklig ist <math>\left(\neg B\right)</math> , dann ist es auch nicht gleichseitig <math>\left( \neg A \right)</math> . | ||
| + | Da diese Implikation stimmt, stimmt auch die Äquivalenz.--[[Benutzer:Der Bohrer|Der Bohrer]] 11:45, 22. Nov. 2012 (CET)<br /> | ||
| + | Warum stimmt die Kontraposition nicht? Es fehl ein Beweis mit Begründung. (Auch wenn es vielleicht nur ein Schritt ist.)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 19:30, 27. Nov. 2012 (CET) | ||
| + | |||
| + | |||
| + | Die Kontraposition wäre: Jedes nicht gleichschenklige Dreieck ist auch nicht gleichseitig. Nicht gleichschenklig bedeutet also |AB|<math>\neq</math> |BC|<math>\neq</math> |AC| solch ein Dreieck <math> \overline{ABC}</math> ist nicht Gleichseitig. Damit ist Die Kontraposition bewiesen und die Äquivalenz stimmt.<br /> | ||
| + | Ist das so möglich? --Würmli 16:48, 3. Feb. 2013 (CET)<br /> | ||
| + | *Ja!--[[Benutzer:Tutorin Anne|Tutorin Anne]] 13:08, 4. Feb. 2013 (CET) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 4. Februar 2013, 13:08 Uhr
a) Definieren Sie die Begriffe: "gleichseitiges Dreieck" und "gleichschenkliges Dreieck". Die Begriffe "Dreieck" und "Seite eines Dreiecks" seien bereits definiert.
Ein gleichseitiges Dreieck ist ein Dreieck, bei dem alle Seiten gleich lang sind.--Der Bohrer 11:45, 22. Nov. 2012 (CET)
Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten.--Der Bohrer 11:45, 22. Nov. 2012 (CET)
Ein gleichschenkliges Dreieck ist ein Dreieck mit einer Symmetrieachse.
Robzimmi, kannst du bitte das nächste Mal deine Signatur anhängen, danke! Ansonsten eine super Idee, Robzimmi!--Tutorin Anne 19:30, 27. Nov. 2012 (CET)
Ein Gleichseitige Dreieck ist ein Dreieck mit drei Symmetrieachsen. --Würmli 16:52, 3. Feb. 2013 (CET)
- Super! (Ich würde noch 'verschiedene' Symmetrieachsen einfügen)--Tutorin Anne 13:08, 4. Feb. 2013 (CET)
b) Beweisen Sie durch Kontraposition: Jedes gleichseitige Dreieck ist auch ein gleichschenkliges Dreieck.
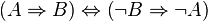Wenn ein Dreieck also nicht gleichschenklig ist 
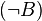, dann ist es auch nicht gleichseitig 
.
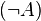Da diese Implikation stimmt, stimmt auch die Äquivalenz.--Der Bohrer 11:45, 22. Nov. 2012 (CET)
Warum stimmt die Kontraposition nicht? Es fehl ein Beweis mit Begründung. (Auch wenn es vielleicht nur ein Schritt ist.)--Tutorin Anne 19:30, 27. Nov. 2012 (CET)
Die Kontraposition wäre: Jedes nicht gleichschenklige Dreieck ist auch nicht gleichseitig. Nicht gleichschenklig bedeutet also |AB|
|BC| |AC| solch ein Dreieck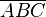 
ist nicht Gleichseitig. Damit ist Die Kontraposition bewiesen und die Äquivalenz stimmt.
Ist das so möglich? --Würmli 16:48, 3. Feb. 2013 (CET)
- Ja!--Tutorin Anne 13:08, 4. Feb. 2013 (CET)
