Lösung von Aufgabe 7.2 WS 12 13: Unterschied zwischen den Versionen
(→Lösung von User Hazel12) |
Yellow (Diskussion | Beiträge) (→Bemerkung m.g.) |
||
| (22 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 20: | Zeile 20: | ||
==Lösung von User Hazel12== | ==Lösung von User Hazel12== | ||
| − | |||
| − | + | === 1. Definition Kugel: === | |
| + | Die Menge aller Punkte P des Raumes, die von einem festen Punkt M den selben Abstand r haben und die Menge der Punkte M und aller Punkte zwischen P und M bilden eine Kugel. | ||
| + | <br /><br />Eine Kugel ist die Menge aller Punkte für die gilt Strecke PM=r. M ist Mittelpunkt und r ist radius. | ||
| − | 2. Definition Kreis: | + | === 2. Definition Kreis: === |
Die Menge aller Punkte P einer Ebene, die von einem festen Punkt M den selben Abstand r haben, bilden einen Kreis. | Die Menge aller Punkte P einer Ebene, die von einem festen Punkt M den selben Abstand r haben, bilden einen Kreis. | ||
| − | 3: | + | |
| + | === 3: === | ||
<u>Sehnen:</u> | <u>Sehnen:</u> | ||
Sehnen sind die Strecken von einem Punkt P e k zu einem anderen Punkt Q e k. | Sehnen sind die Strecken von einem Punkt P e k zu einem anderen Punkt Q e k. | ||
| Zeile 39: | Zeile 41: | ||
Radien sind die Strecken von P e k zum Mittelpunkt von k. | Radien sind die Strecken von P e k zum Mittelpunkt von k. | ||
| − | 4: | + | |
| + | === 4: === | ||
<u>Passante:</u> | <u>Passante:</u> | ||
Eine Passante ist eine Gerade, die in der selben Ebene liegt, wie ein Kreis k und die k in keinem einzigen Punkt schneidet oder berührt. | Eine Passante ist eine Gerade, die in der selben Ebene liegt, wie ein Kreis k und die k in keinem einzigen Punkt schneidet oder berührt. | ||
| Zeile 50: | Zeile 53: | ||
| − | |||
| + | === 5: === | ||
| − | 6: | + | === 6: Definition Großkreis: === |
| − | ==Lösung von User ...== | + | Ein Großkreis ist ein größtmöglicher Kreis auf einer Kugeloberfläche. Sein Mittelpunkt fällt immer mit dem Mittelpunkt der Kugel zusammen. (wikipedia) |
| + | |||
| + | ==Lösung von User Yellow== | ||
| + | 5. Es sei E eine Ebene und s eine Kugel. Wenn E und s einen Punkt gemeinsam haben, dann ist E eine Tangentialebene von s.<br /><br /> | ||
| + | 6. Es sei k ein Kreis und s eine Kugel des selben Raums. Wenn alle Punkte von k mit s inzidieren und der Radius von k identisch ist mit dem Radius von s, dann ist k ein Großkreis von s<br /> ( muss ich ein und deselben Raums mit einbringen oder könnte man das auch weglassen?) | ||
| + | |||
| + | --[[Benutzer:Yellow|Yellow]] 09:09, 10. Dez. 2012 (CET) | ||
| + | ) | ||
| + | |||
| + | ==Bemerkung m.g.== | ||
| + | @ Yellow: | ||
| + | |||
| + | *Eine Tangentialebene wäre nach Ihrer Definition auch im folgenden Fall gegeben:<br /> | ||
| + | [[Datei:Kugel_Ebene.jpg]]<br /> | ||
| + | |||
| + | Es ist die Sache mit dem Bier: <br />Sie: Wo warst du? <br />Er: Ich habe ein Bier getrunken. <br />Sie: Lüg nicht, es waren mehr als eins, wenigstens 10. <br />Er: Ich habe nicht gelogen. Hätte ich gesagt, dass ich genau ein Bier getrunken habe, hätte ich gelogen. Um 10 Bier zu trinken muss man aber erst mal ein Bier trinken.--[[Benutzer:*m.g.*|*m.g.*]] 12:55, 10. Dez. 2012 (CET) | ||
| + | |||
| + | |||
| + | *Großkreis: | ||
| + | Es gibt für uns nur einen Raum. (Irgendwo haben wir definiert: Die Menge aller Punkte heißt Raum.) Alles korrekt also.<br /><br /> | ||
| + | @ Hazel12: | ||
| + | *Großkreis: Größtmöglicher Kreis auf der Kugel. Die Wikipedia belässt es häufig bei informellen Definitionen. Was bedeutet ein Kreis ist größer als ein anderer? | ||
<!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | <!--- Das, was hier drunter steht muss stehen bleiben, also oberhalb dieses Kommentars Änderungen einfügen ---> | ||
| Zeile 63: | Zeile 87: | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
| + | @ hazel Def Kugel Kann man Element des Raumes nicht weglassen. wir gehen doch immer vom Raum aus wenn nichts dabei steht???? | ||
| + | <br /> | ||
| + | |||
| + | Ok 2.Versuch<br /> | ||
| + | 5. Es sei E eine Ebene und s eine Kugel. Wenn E und s genau einen Punkt gemeinsam haben, dann ist E eine Tangentialebene von s. | ||
| + | |||
| + | --[[Benutzer:Yellow|Yellow]] 12:27, 11. Dez. 2012 (CET) | ||
Aktuelle Version vom 11. Dezember 2012, 12:27 Uhr
|
Aufgabe 7.2Definieren Sie:
BemerkungDer Äquator und alle Längenkreise der Erdkugel sind Beispiele für Großkreise.
Lösung von User Hazel121. Definition Kugel:Die Menge aller Punkte P des Raumes, die von einem festen Punkt M den selben Abstand r haben und die Menge der Punkte M und aller Punkte zwischen P und M bilden eine Kugel.
2. Definition Kreis:Die Menge aller Punkte P einer Ebene, die von einem festen Punkt M den selben Abstand r haben, bilden einen Kreis.
3:Sehnen: Sehnen sind die Strecken von einem Punkt P e k zu einem anderen Punkt Q e k. Durchmesser: Durchmesser sind die Strecken von P e k zu Q e k, die durch M, den Mittelpunkt von k gehen. P,M und Q sind kollinear. Radien: Radien sind die Strecken von P e k zum Mittelpunkt von k.
4:Passante: Eine Passante ist eine Gerade, die in der selben Ebene liegt, wie ein Kreis k und die k in keinem einzigen Punkt schneidet oder berührt. Tangente: Eine Tangente ist eine Gerade, die einen Kreis k in genau einem Punkt P berührt. P e k. Sekante: Eine Sekante ist eine Gerade, die einen Kreis k in genau zwei paarweise verschiedenen Punkten P und Q schneidet. P e k und Q e k.
5:6: Definition Großkreis:Ein Großkreis ist ein größtmöglicher Kreis auf einer Kugeloberfläche. Sein Mittelpunkt fällt immer mit dem Mittelpunkt der Kugel zusammen. (wikipedia) Lösung von User Yellow5. Es sei E eine Ebene und s eine Kugel. Wenn E und s einen Punkt gemeinsam haben, dann ist E eine Tangentialebene von s. --Yellow 09:09, 10. Dez. 2012 (CET) ) Bemerkung m.g.@ Yellow:
Es ist die Sache mit dem Bier:
Es gibt für uns nur einen Raum. (Irgendwo haben wir definiert: Die Menge aller Punkte heißt Raum.) Alles korrekt also.
|
@ hazel Def Kugel Kann man Element des Raumes nicht weglassen. wir gehen doch immer vom Raum aus wenn nichts dabei steht????
Ok 2.Versuch
5. Es sei E eine Ebene und s eine Kugel. Wenn E und s genau einen Punkt gemeinsam haben, dann ist E eine Tangentialebene von s.
--Yellow 12:27, 11. Dez. 2012 (CET)
 und dem Radius
und dem Radius 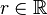 ,
,
 (Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),
(Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),


