Lösung von Aufgabe 7.2 WS 12 13: Unterschied zwischen den Versionen
(→1. Definition Kugel:) |
Yellow (Diskussion | Beiträge) (→Bemerkung m.g.) |
||
| Zeile 88: | Zeile 88: | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
@ hazel Def Kugel Kann man Element des Raumes nicht weglassen. wir gehen doch immer vom Raum aus wenn nichts dabei steht???? | @ hazel Def Kugel Kann man Element des Raumes nicht weglassen. wir gehen doch immer vom Raum aus wenn nichts dabei steht???? | ||
| + | <br /> | ||
| + | |||
| + | Ok 2.Versuch<br /> | ||
| + | 5. Es sei E eine Ebene und s eine Kugel. Wenn E und s genau einen Punkt gemeinsam haben, dann ist E eine Tangentialebene von s. | ||
| + | |||
| + | --[[Benutzer:Yellow|Yellow]] 12:27, 11. Dez. 2012 (CET) | ||
Aktuelle Version vom 11. Dezember 2012, 12:27 Uhr
|
Aufgabe 7.2Definieren Sie:
BemerkungDer Äquator und alle Längenkreise der Erdkugel sind Beispiele für Großkreise.
Lösung von User Hazel121. Definition Kugel:Die Menge aller Punkte P des Raumes, die von einem festen Punkt M den selben Abstand r haben und die Menge der Punkte M und aller Punkte zwischen P und M bilden eine Kugel.
2. Definition Kreis:Die Menge aller Punkte P einer Ebene, die von einem festen Punkt M den selben Abstand r haben, bilden einen Kreis.
3:Sehnen: Sehnen sind die Strecken von einem Punkt P e k zu einem anderen Punkt Q e k. Durchmesser: Durchmesser sind die Strecken von P e k zu Q e k, die durch M, den Mittelpunkt von k gehen. P,M und Q sind kollinear. Radien: Radien sind die Strecken von P e k zum Mittelpunkt von k.
4:Passante: Eine Passante ist eine Gerade, die in der selben Ebene liegt, wie ein Kreis k und die k in keinem einzigen Punkt schneidet oder berührt. Tangente: Eine Tangente ist eine Gerade, die einen Kreis k in genau einem Punkt P berührt. P e k. Sekante: Eine Sekante ist eine Gerade, die einen Kreis k in genau zwei paarweise verschiedenen Punkten P und Q schneidet. P e k und Q e k.
5:6: Definition Großkreis:Ein Großkreis ist ein größtmöglicher Kreis auf einer Kugeloberfläche. Sein Mittelpunkt fällt immer mit dem Mittelpunkt der Kugel zusammen. (wikipedia) Lösung von User Yellow5. Es sei E eine Ebene und s eine Kugel. Wenn E und s einen Punkt gemeinsam haben, dann ist E eine Tangentialebene von s. --Yellow 09:09, 10. Dez. 2012 (CET) ) Bemerkung m.g.@ Yellow:
Es ist die Sache mit dem Bier:
Es gibt für uns nur einen Raum. (Irgendwo haben wir definiert: Die Menge aller Punkte heißt Raum.) Alles korrekt also.
|
@ hazel Def Kugel Kann man Element des Raumes nicht weglassen. wir gehen doch immer vom Raum aus wenn nichts dabei steht????
Ok 2.Versuch
5. Es sei E eine Ebene und s eine Kugel. Wenn E und s genau einen Punkt gemeinsam haben, dann ist E eine Tangentialebene von s.
--Yellow 12:27, 11. Dez. 2012 (CET)
 und dem Radius
und dem Radius 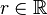 ,
,
 (Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),
(Durchmesser und Radius sind als geometrische Objekte und nicht als Zahlen zu verstehen),


