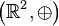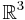Isomorphie von Gruppen 2012 13: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Pfeilklassen des Raumes und \mathbb{R}^3)
 
Zeile 15: Zeile 15:
 
Behauptung: <math>\varphi</math> ist ein Gruppenisomorphismus von <math>\left(\mathbb{P}_2, +\right)</math> auf <math>\left(\mathbb{R}^2, \oplus\right)</math>
 
Behauptung: <math>\varphi</math> ist ein Gruppenisomorphismus von <math>\left(\mathbb{P}_2, +\right)</math> auf <math>\left(\mathbb{R}^2, \oplus\right)</math>
 
==Pfeilklassen des Raumes und <math>\mathbb{R}^3</math>==
 
==Pfeilklassen des Raumes und <math>\mathbb{R}^3</math>==
−
 
+
analog zum zweidimensionalen Fall
 
<!--- hier drunter nichts eintragen --->
 
<!--- hier drunter nichts eintragen --->
 
[[Kategorie:Linalg]]
 
[[Kategorie:Linalg]]

Aktuelle Version vom 12. Dezember 2012, 19:44 Uhr

Inhaltsverzeichnis

Definition

Definition

(Gruppenisomorphismus)
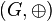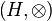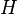Es seien \left(G, \oplus \right) und \left(H, \otimes \right) zwei Gruppen. Wenn eine Bijektion \varphi von G auf H derart existiert, dass
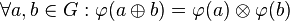\forall a, b \in G: \varphi(a \oplus b) = \varphi(a) \otimes \varphi(b) gilt, dann sind die beiden Gruppen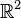 \left(G, \oplus \right) und \left(H, \otimes \right) isomorph zueinander. Die Abbildung \varphi heißt Gruppenisomorphismus.

Beispiele

Vierergruppen

ergänzen Sie selbst ...

Pfeilklassen der Ebene und \mathbb{R}^2

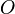Wir legen der Ebene ein kartesisches Koordinatensystem K mit dem Koordinatenursprung O zugrunde. Wir repräsentieren jetzt jede Pfeilklasse durch ihren Repräsentanten mit dem Anfangspunkt 0. Jetzt definiren wir die folgende Abbildung \varphi von der Menge der Pfeilklassen auf \mathbb{R}^2:

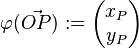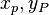  • \varphi (\vec{OP}) := \begin{pmatrix} x_P \\ y_P \end{pmatrix} mit x_p, y_P sind die Kordnaten von P bzgl. K.

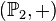Behauptung: \varphi ist ein Gruppenisomorphismus von \left(\mathbb{P}_2, +\right) auf \left(\mathbb{R}^2, \oplus\right)

Pfeilklassen des Raumes und \mathbb{R}^3

analog zum zweidimensionalen Fall

Von „http://geometrie.zum.de/index.php?title=Isomorphie_von_Gruppen_2012_13&oldid=19616“