Der Basiswinkelsatz WS 12 13: Unterschied zwischen den Versionen
RM2208 (Diskussion | Beiträge) (→Definition VIII.1 : (gleichschenkliges Dreieck)) |
(→Satz VIII.1: (Basiswinkelsatz)) |
||
| Zeile 53: | Zeile 53: | ||
|- | |- | ||
|} | |} | ||
| + | |||
| + | |||
| + | Begründungen: | ||
| + | |||
| + | '''zu 1''') Voraussetzung | ||
| + | '''zu 2)''' Konstruktion, 1) und Def. Mittelsenkrechte | ||
| + | '''zu 3)''' Involutorische Abbildung: A und B sind symmetrischliegende Punkte, A wird auf B gespiegelt und B auf A | ||
| + | '''zu 4)''' 3), C wird auf sich selbst gespiegelt | ||
| + | '''zu 5)''' 3),4) M wird auf sich selbst gespiegelt | ||
| + | |||
| + | ''sind C und M nicht auch Fixpunkte? | ||
| + | '' | ||
| + | '''zu 6)''' Def. Winkelkongruenz bei Geradenspiegelung | ||
Aktuelle Version vom 19. Januar 2013, 13:44 Uhr
Inhaltsverzeichnis |
Der Basiswinkelsatz
Gleichschenklige Dreiecke
Definition VIII.1 : (gleichschenkliges Dreieck)
Das können sie selbst. Bringen Sie in der Definition die Begriffe Basis, Basiswinkel und Schenkel eines gleichschenkligen Dreiecks unter.
Übungsaufgabe
Ein gleichschenkliges Dreieck ist ein Dreieck mit zwei gleich langen Seiten. Die beiden gleich langen Seiten heißen Schenkel, die dritte Seite heißt Basis. Die an die Basis anliegenden Winkel heißen Basiswinkel --RM2208 21:10, 11. Jan. 2013 (CET).
Der Basiswinkelsatz
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweis:
Voraussetzung: Das können Sie selbst:
Behauptung: Auch das sollte kein Problem sein:
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 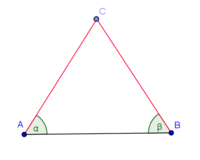
|
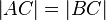
|
Begründung? |
| (2) | 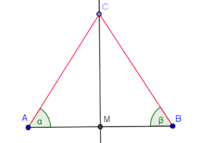
|
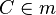 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
Begründung? |
| (3) | |
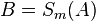
|
Begründung? |
| (4) | |
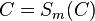
|
Begründung? |
| (5) | |
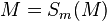
|
Begründung? |
| (6) | |
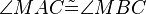
|
Begründung? |
Begründungen:
zu 1) Voraussetzung zu 2) Konstruktion, 1) und Def. Mittelsenkrechte zu 3) Involutorische Abbildung: A und B sind symmetrischliegende Punkte, A wird auf B gespiegelt und B auf A zu 4) 3), C wird auf sich selbst gespiegelt zu 5) 3),4) M wird auf sich selbst gespiegelt
sind C und M nicht auch Fixpunkte? zu 6) Def. Winkelkongruenz bei Geradenspiegelung

