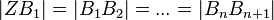Projektionssatz: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Jessy* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „Es seien a und b zwei Geraden, die sich in Z schneiden. Auf a ist eine Folge von Punkten festgelegt mit: <math> |ZA_1| = |A_1A_2| = ... = |A_nA_{n+1}| </math><br …“) |
Jessy* (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <u>'''Def.(Parallelprojektion einer Ebene auf eine Gerade der Ebene):'''</u><br /> | ||
| + | Es seien <math> \varepsilon </math> eine Ebene und b eine Gerdae dieser Ebene. Ferner sei r eine Gerade der Ebene <math> \varepsilon </math>, die nicht parallel zu b ist.<br /> | ||
| + | Unter der Parallelprojektion von <math> \varepsilon </math> auf b mit der Richtung r versteht man eine Abbildung <math> \varphi </math> der Punkte der Ebene <math> \varepsilon </math> auf b mit folgenden Eigenschaften:<br /> | ||
| + | <math> \forall P \in \varepsilon : \varphi (P) = s \cap b </math> mit <math> P \in s \wedge s\parallel r </math><br /><br /> | ||
| + | |||
| + | === Projektionssatz: === | ||
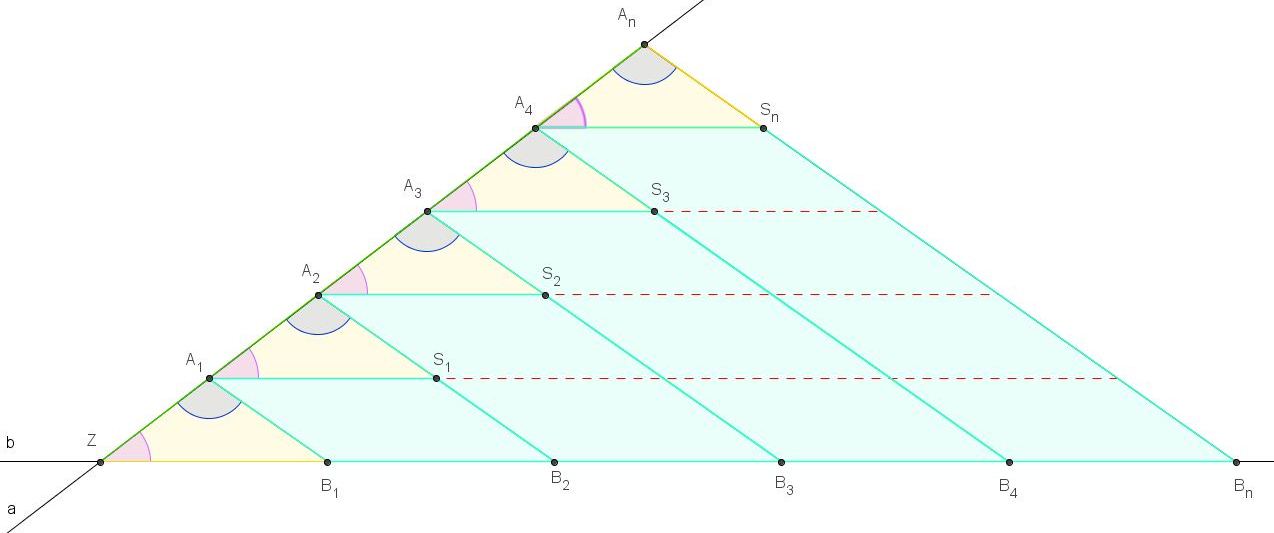
Es seien a und b zwei Geraden, die sich in Z schneiden. Auf a ist eine Folge von Punkten festgelegt mit: <math> |ZA_1| = |A_1A_2| = ... = |A_nA_{n+1}| </math><br /> | Es seien a und b zwei Geraden, die sich in Z schneiden. Auf a ist eine Folge von Punkten festgelegt mit: <math> |ZA_1| = |A_1A_2| = ... = |A_nA_{n+1}| </math><br /> | ||
<math> B1,B_2, ... B_n </math> seien die Bilder von <math> A_1, A_2, ..., A_n </math> bei einer Parallelprojektion.<br /> | <math> B1,B_2, ... B_n </math> seien die Bilder von <math> A_1, A_2, ..., A_n </math> bei einer Parallelprojektion.<br /> | ||
Es gilt: <math> |ZB_1| = |B_1B_2| = ... = |B_nB_{n+1}|</math><br /><br /> | Es gilt: <math> |ZB_1| = |B_1B_2| = ... = |B_nB_{n+1}|</math><br /><br /> | ||
| + | [[Bild:Projektionssatz.JPG]]<br /><br /> | ||
| + | |||
| + | === Beweis des Projektionssatzes === | ||
Aktuelle Version vom 16. Januar 2013, 09:50 Uhr
Def.(Parallelprojektion einer Ebene auf eine Gerade der Ebene):
Es seien 
eine Ebene und b eine Gerdae dieser Ebene. Ferner sei r eine Gerade der Ebene , die nicht parallel zu b ist.
Unter der Parallelprojektion von auf b mit der Richtung r versteht man eine Abbildung 
der Punkte der Ebene auf b mit folgenden Eigenschaften:
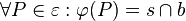mit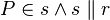 
Projektionssatz:
Es seien a und b zwei Geraden, die sich in Z schneiden. Auf a ist eine Folge von Punkten festgelegt mit: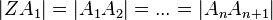 
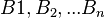seien die Bilder von 
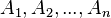bei einer Parallelprojektion.
Es gilt: 
