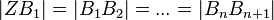Projektionssatz
Aus Geometrie-Wiki
Def.(Parallelprojektion einer Ebene auf eine Gerade der Ebene):
Es seien  eine Ebene und b eine Gerdae dieser Ebene. Ferner sei r eine Gerade der Ebene
eine Ebene und b eine Gerdae dieser Ebene. Ferner sei r eine Gerade der Ebene  , die nicht parallel zu b ist.
, die nicht parallel zu b ist.
Unter der Parallelprojektion von  auf b mit der Richtung r versteht man eine Abbildung
auf b mit der Richtung r versteht man eine Abbildung  der Punkte der Ebene
der Punkte der Ebene  auf b mit folgenden Eigenschaften:
auf b mit folgenden Eigenschaften:
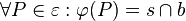 mit
mit 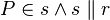
Projektionssatz:
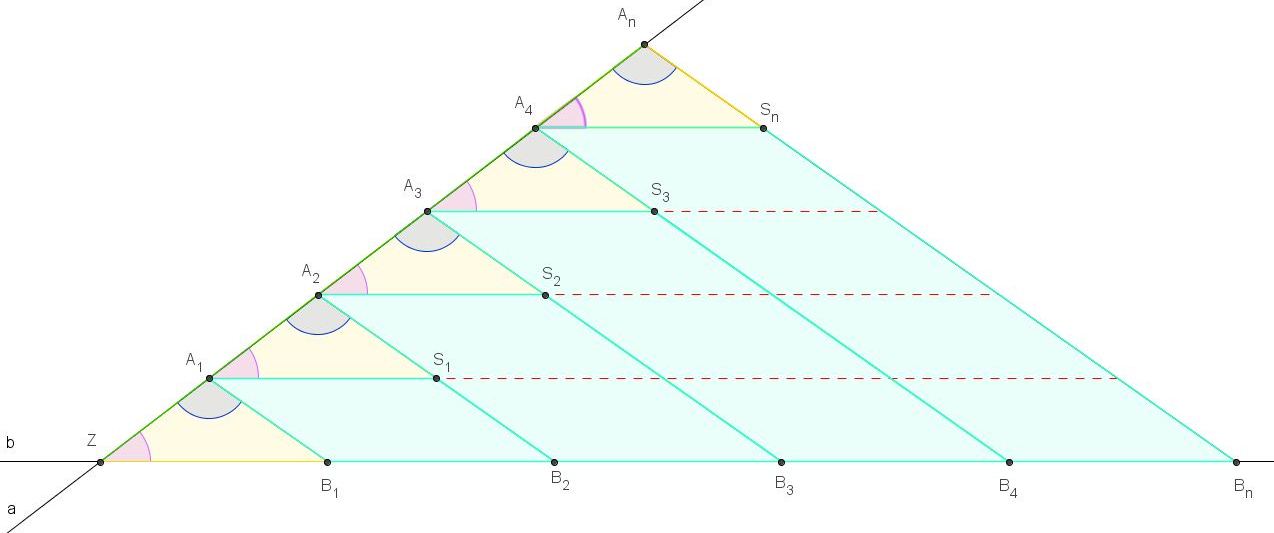
Es seien a und b zwei Geraden, die sich in Z schneiden. Auf a ist eine Folge von Punkten festgelegt mit: 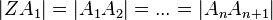
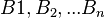 seien die Bilder von
seien die Bilder von 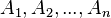 bei einer Parallelprojektion.
bei einer Parallelprojektion.
Es gilt: