Lösung von Zusatzaufgabe 6.1P (WS 12 13): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (4 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 13: | Zeile 13: | ||
!Beweisschritt!!Begründung | !Beweisschritt!!Begründung | ||
|- | |- | ||
| − | | 1 | + | | 1 <math>|AB| + |BC| = |AC|</math> || Voraussetzung, Def. Zwischenrelation |
|- | |- | ||
| − | | 2 <math>B \in | + | | 2 <math>B \in \overline{AC} </math> || 1.) |
|- | |- | ||
| − | | 3 <math>A, B, C \in | + | | 3 <math>A, B, C \in AC </math> || 1,) ; 2,) |
|- | |- | ||
| 4 koll (A,B,C) || 3.); Def. koll | | 4 koll (A,B,C) || 3.); Def. koll | ||
|} | |} | ||
<br /> | <br /> | ||
| − | Ich bin mir aber nicht sicher, ob man das so machen kann, kommt mir irgendwie zu primitiv vor...--[[Benutzer:Unicycle|Unicycle]] 22:13, 17. Jan. 2013 (CET) | + | Ich bin mir aber nicht sicher, ob man das so machen kann, kommt mir irgendwie zu primitiv vor...--[[Benutzer:Unicycle|Unicycle]] 22:13, 17. Jan. 2013 (CET)<br /> |
| + | *Du hast nicht begründet, wie du auf den zweiten Schritt kommst. Wo steht denn das? | ||
| + | * Tipp: Schaut euch mal an, was unter Dreiecksungleichung steht.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:44, 18. Jan. 2013 (CET)<br /><br /> | ||
| + | Hier fehlt noch etwas vor Schritt 2)<br /><br /> | ||
| + | Man muss hier eine Fallunterscheidung machen:<br /> | ||
| + | Fall1: <math>|AB| + |BC| > |AC|\Rightarrow</math> <math>\exists</math> Dreieck ABC -> ist zu verwerfen,da Widerspruch zu 1.)<br /> | ||
| + | Fall2: <math>|AB| + |BC| = |AC|\Rightarrow</math> <math>\neg \exists</math> Dreieck ABC -> ist anzunehmen, daraus folgt dann Punkt 2<br /> | ||
| + | Begründung: Dreiecksungleichung, 1.)<br /> | ||
| + | --[[Benutzer:TobiWan|TobiWan]] 14:15, 19. Jan. 2013 (CET)<br /> | ||
| + | * Die Idee stimmt. Es lässt sich sogar einfacher noch, ohne die Fallunterscheidung zu machen, direkt daraus ableiten, dass die Punkte kollinear sind. (Genau so steht's ja in der Dreiecksungleichung.) Die oben genannte Schritte 2 + 3 brauch man dann gar nicht mehr.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 12:27, 20. Jan. 2013 (CET) | ||
[[Kategorie:Einführung_P]] | [[Kategorie:Einführung_P]] | ||
Aktuelle Version vom 20. Januar 2013, 12:27 Uhr
Beweisen Sie: Aus 
folgt 
.
Zum Verwenden von mathematischen Zeichen, kann man den Formeleditor öffnen (Symbol ganz links, Summenzeichen). Als Hilfestellung schon mal eine Tabelle. --Tutorin Anne 12:38, 10. Dez. 2012 (CET)
| Voraussetzung | Zw (A,B,C) |
| Behauptung | koll (A,B,C) |
| Beweisschritt | Begründung |
|---|---|
1  |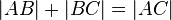
Voraussetzung, Def. Zwischenrelation |
2  |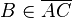
1.) |
3  |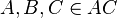
1,) ; 2,) |
| 4 koll (A,B,C) | 3.); Def. koll |
Ich bin mir aber nicht sicher, ob man das so machen kann, kommt mir irgendwie zu primitiv vor...--Unicycle 22:13, 17. Jan. 2013 (CET)
- Du hast nicht begründet, wie du auf den zweiten Schritt kommst. Wo steht denn das?
- Tipp: Schaut euch mal an, was unter Dreiecksungleichung steht.--Tutorin Anne 18:44, 18. Jan. 2013 (CET)
Hier fehlt noch etwas vor Schritt 2)
Man muss hier eine Fallunterscheidung machen:
Fall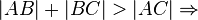1: 
Dreieck ABC -> ist zu verwerfen,da Widerspruch zu 1.)
Fall2: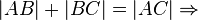 
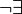Dreieck ABC -> ist anzunehmen, daraus folgt dann Punkt 2
Begründung: Dreiecksungleichung, 1.)
--TobiWan 14:15, 19. Jan. 2013 (CET)
- Die Idee stimmt. Es lässt sich sogar einfacher noch, ohne die Fallunterscheidung zu machen, direkt daraus ableiten, dass die Punkte kollinear sind. (Genau so steht's ja in der Dreiecksungleichung.) Die oben genannte Schritte 2 + 3 brauch man dann gar nicht mehr.--Tutorin Anne 12:27, 20. Jan. 2013 (CET)
