Benutzer:Andreas: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: Bild:Weinberge_und_ihre_Parallelität.JPG)
 
 
(35 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
−
[[Bild:Weinberge_und_ihre_Parallelität.JPG]]
+
<gallery>
 +
 
 +
Bild:Weinberge_und_ihre_Parallelität.JPG
 +
Bild:Geometrie Kugel Andreas.JPG
 +
</gallery><br />
 +
[[Spiegelung_Test]]<br />
 +
[[Prinzip des Cavalieri und Volumen Kugel]]<br />
 +
<br />
 +
== Satz: Jede Drehung <math>D_{Z,\beta}</math> ist eine Bewegung. ==
 +
<ggb_applet width="547" height="470"  version="3.2" ggbBase64="UEsDBBQACAAIAHdxaT0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnLcts2FF03X8HhojvTePE1lZxp001m0vqVZuEdREISaopUSdCW/Ffxh/ibegGQEiVZsuQ6TVWOPRQvwIuLc+4Lw9772SRz7kRZySLvu9hDriPypEhlPuq7tRqeRO77s3e9kShGYlByZ1iUE676LvWIq+W1PHv3Q68aF/cOz8yUL1Lc990hzyrhOtW0FDytxkKoFTmvZzKTvJyfD/4UiaqWA1bJx3xawyqqrEGWTNJPsmofT82C00yqX+WdTEXpZEXSdwMfTIdfX0SpZMKzvsuQlZC+S9YGQUT16Lgo5UORKz19qXwIEsep5IMARIiW9U7NRnuiTjKZSp7rzRg7YJLj3MtUjfuuz0JQKeRoDLayILLakqIo0+t5pcTEmd2IsgBzCPUC4rvOvHkOfE8/VmCaXjOIvFCPrj4bbeLuWigF7FQOn4klbqNSpisPH6tfimwpmhYyVx/4VNWloZY2oms110sAFqW2++d8lIlGRgD5sUhuB8Xs2mJBrerP86l5xRg0GH0osqJ0So0yGD1q7gN7N3O0pYtZyMxBZkajQytdjOOYmBnmPrB3MyuTuTWt2Tlud41Ru4ysHC0A5dojF5vP+EAAw65T51J9ah/AE26brWL7wu/1ZACh0PWFhU78Vjp7p2te1LsVZS4y6ys5cFsXdeXcaZ+0axlDUpHICTzagQYSrun6Awyw0lSMStEabgPJAmZGUdcf18S909YIbUMFtiYKMgLsR+m96IBVECz6V8qVluhoyMREQKgo4w/GnRa43LiLvFCYEG+DuRlfIgzDz/qG8SKeTcccJF5jfMbnEPDd7Rh958NhJZQz67snBHCfw9txZ/i3Il3FgOeApdkghOVU69dsTYVImxyoGhd3prCiCZgOFQbByqyGvNgsZ3882LfNJBtdOj2YhWlDvYXsBfAu/lXwvhk62GN45bJQgYqYdi//7ZC7/L8g57Ooe/kGOuT5IaLdv8OQS4rJhOepk/MJWHHF5wYtqWutw5EOWodj7X4WoVq1A9xqat7f4KAETS3C3F3N1WoMKTEXVWUKiuqWju00dUDZxhN6PUtLnIGfVVfUFVxnD4+ue+6DlhIfmorlxdYL047Nir9yO6ey5UFOoIVJpFpgnWl/+JgrKBbCJN/NGnArxFQX3/P8c8nzSvdidk6nthxK9uUG2YP9yR4cE9mQeNhG+Biy2WqwMcM28qIIBZ3riNg2bdwa3xeWb007eY72p6+7eTe9xoI0mK3fB3vqFm9oaRmOEWUspLHvxy/xvisXY7RJPN6zBaA2hk92dgB7scjLZJlNF81slhX3V2KYiZmBeV9OrsVIy9dYudyWcpPdbFSNthbM5JgiEXtBsBKHYdtEYRp2L9+2BicQonFEURjhKIaDG0Ph8cTiVaGgY36e9pPQ112BDsibDQ+4/JFPi+qn3X6w1v40r3zXJqhbXsMoRBGNsB8FEQ0xMzxDHkYsBkZjhgmNfJ/8ozbmOXwv9sD34nB8L/5b+GKPIp9ANOCQEhTG+sTcxFGE4zjSEoR85kcHtth7Za4GC5u/lliuZrF9MN7IZR2UjyajgYfHDP4pJYwh3PbrQIQfxAgz4ImEkU1n2IvDELEA4yAOGCFRcDzp7HlnuNntBulhDpAeE/UQbSGOEMIQahBwzGekaSvJanA2IUgh42HfD7SzEHxMZ4id1F9uoV4cRr04KurhnLhayZr6FmyUvQfjKEA7eAKcQhiJY+ofEffPnii6FaA9V2xxg6ev+1SC9TNGpxDsOmng73XUIPYEeULCXQ5z+FkjbIWvPGu8fP7blqmfHg9i6HGTGxpHhNAgCiDJQWcfvY6b9lvCody8AfjxNwD/cr8geXxFkDxuC5I1IsKjI0JH5oFMnHa/Xpjvds2Hy7O/AVBLBwhr4XgMiQUAAOocAABQSwECFAAUAAgACAB3cWk9a+F4DIkFAADqHAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAMMFAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" /><br />
 +
 
 +
==Beweis==
 +
Voraussetzung: Drehung D um Punkt Z mit dem Winkel <math>\beta</math><br />
 +
Behauptung: |PQ|=|P'Q'|
 +
 
 +
{| class="wikitable "
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
| 1) <math>\overline {ZP} \tilde = \overline {ZP'}</math>
 +
| folgt unmittelbar aus der Definition: (Drehung)
 +
|-
 +
| 2) <math>\overline {ZQ} \tilde = \overline {ZQ'}</math>
 +
| folgt unmittelbar aus der Definition: (Drehung)
 +
|-
 +
| 3) <math>\angle {PZP'} \tilde = \angle {QZQ'}</math>
 +
| folgt unmittelbar aus der Definition: (Drehung)
 +
|-
 +
| 4) <math>|\alpha'|=|\beta'|+|\alpha - \beta|</math><br />
 +
<math>|\alpha'|= |\alpha|</math><br />
 +
| rechnen in den reellen Zahlen, folgt aus Schritt 3, da <math>\beta = \angle {PZP'} </math> und <math> \beta' = \angle {QZQ'}</math>
 +
|-
 +
| 5) <math>\triangle {ZPQ} \tilde = \triangle {ZP'Q'}</math>
 +
| folgt aus den Schritten 1-4, sws
 +
|-
 +
| 6) <math>\overline {PQ} \tilde = \overline {P'Q'}</math>
 +
| folgt aus Schritt 5
 +
|-
 +
| 7) <math>|PQ|=|P'Q'|</math>
 +
| folgt aus Schritt 6, q.e.d
 +
|-
 +
 
 +
|}
 +
--[[Benutzer:Andreas|Andreas]] 14:22, 9. Nov. 2010 (UTC)
 +
 
 +
==Satz: Wenn eine Bewegung <math>\phi</math> genau einen Fixpunkt Z hat, dann ist <math>\phi</math> eine Drehung um den Fixpunkt Z.==
 +
 
 +
<ggb_applet width="529" height="343"  version="3.2" ggbBase64="UEsDBBQACAAIAMF8az0AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VnNcts2ED43T8HhoTfR+Cc5lZJp00tm0saO0xxy6UAkJLGmSJWEbMlvlTxInqkLgJQpyVLkn8RWfbDEBbgAvm93v6XYf7WY5t6lquqsLAY+DpDvqSIp06wYD/y5HvUi/9XLF/2xKsdqWElvVFZTqQc+DYhv7PPs5Yuf+vWkvPJkbqd8zNTVwB/JvFa+V88qJdN6opRes8v5IsszWS3fDf9Ria5vBpyTN8VsDqvoag62ZJq+zer28sQuOMsz/Xt2maWq8vIyGfiCw9bh20dV6SyR+cBnyFnIwCcbg2CiZnRSVtl1WWgz/cb5CCyeV2fXChAhxtY/sQftq3mSZ2kmC3MYuw+Y5HlXWaonA5+TGFyqbDwxADHsvCVlWaXny1qrqbf4pKoSthMxA/SyuRLcXNWwL1iQIzvUvbJu1OW50hpoqT25UDeAjassXbt4U/9W5jemWZkV+rWc6XllOaWN6VwvzQKwVmU2/GsxzlVjIwD5RCUXw3Jx7kCgzvWH5czeYjc0HL8u87LyKgMvhwnN59B92jlmp6tZyM5BdkbjwzhdjeOY2Bn2c+g+7aw8K9zWmpPj9tQYtctktWcMBkYIxdXhczlUQK3vzYtMv20vIAQumqNid8Of8+kQcqAbBCuf+LF89k82wqd/oapC5S5ICuB2Xs5r79IEo1vLbiRVSTaFSzfQQCINXX/BBpw1VeNKtRt3GeQAs6OoG4gb5v5Juwmzhxr2mmgoBXAebc5iMlVDlphvqdTGYtIgV1MFOaJtPNhwWuFy6q8KQmlzu83iZvwGYRi+NTZsFMl8NpFgacM/l0vI9O5xrL8/ynT9kLIAsOwJIOFmxoGhY6ZU2lQ33cSwNwOXNiM6WFuIam8BxSNgkIUDvwc3Rb537e62k1z6mMS3C9OGW4fJN9D59EPReTca1Uqb4/QIssfB5EeA10NBLFr4KHk8+M6eCD7s0It/BHgkIBHq/hG7NrlzHCbldCqL1CvkFNZ9L5cWvMwoqyeRiUVPYpOwDrC5bgek89Tcv0VJBZ5awKW/XqD1BOpgoeraqoju6sVu1jow7KIN3b8irIUlcVnNAyosmCKIGOvAjTcVZ8+B1L+Fm1O7up9NoSlJMr3CMzcsvyk0qICyVXW7uF8oNTOq+q74UMmiNt2Vm9MRjbsSerZF6PBwQodHRSgN2FqqIEcvtTy7XMFr2cSOh99zNTb2DY7PdiVtsp/juvHWUpQcE880wKIpgtipSQ/jQGDWYX+rV3y+zL4vNbRStxMb2fZfEpPNmxSf/SxnZf3L33g/1RuSubrpSfuyrr4hgbkQIafwDBYLJ289FsSYc8wjEYaCsfhhYncbwqffRvj0PgifPjeETdOFKWaEcoQoFxF3EItAhDSkAsMAR0LQR4e4CeLeAVF8jxh+qt45alpZfCD8LBCxiEKBYkrDMI5d5x1wwqKIgFXwKA7Z94rvveCf3h380ycAf39whzEiKIoRjTH8Z3Gj+XGEQo4IExyFMUEPiu4d4ttA4ST4Bsp1IT4E4i057oB8JKLcIwHjplwLKiIWxYB7o9Ex1BYRAjeMxyjirFFsDg+FIaGEMOjJ4uNS7J299o4gSA/vuNMjI908MK2VsaVtxEFXOiWvyb5eGIDMQISELOIUVP//wPmuxFeHc66OinN4Wkbd0ood5yiI6GYhvrZtBo4g83kcxRFBUCKOh3P7K/jtsvrJSer2w/XXz/t5tz/VrkiD2eZ+2M+8xTuAfjdkVHBOoffl7XuD+2ktRtvM473Md37lahqdvT9zHUSjrJKO1LbGPC+v3qtRrhYW5weR0lXilpodefn18yGKvElTR5CfJVk981LGtqVHQNfZYUR9uQdRX24nCgciwgyKEwgSZYIwej+i2ldbDyCKNETRvc8PdydKfI+8WiNql9J9/XI3ip4vOSx03BD2uNzEd+bmpPv6zb5xbl65v/wPUEsHCKvppQu1BQAApB8AAFBLAQIUABQACAAIAMF8az2r6aULtQUAAKQfAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA7wUAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" allowRescaling = "true" />
 +
 
 +
==Beweis==
 +
Voraussetzung: <math>\phi </math> ist eine Bewegung, <math>\phi </math> hat genau eine Fixpunkt Z<br />
 +
Behauptung: <math>\beta \cong \beta'</math>
 +
{| class="wikitable "
 +
! Beweisschritt
 +
! Begründung
 +
|-
 +
| 1. <math>P \ne P', Q \ne Q'</math>
 +
| folgt unmittelbar aus der Voraussetzung (genau ein Fixpunkt Z)
 +
|-
 +
| 2. <math>\overline {ZP} \cong \overline {ZP'}</math>
 +
| folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend)
 +
|-
 +
| 3. <math>\overline {ZQ} \cong \overline {ZQ'}</math>
 +
| folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend)
 +
|-
 +
| 4. <math>\overline {PQ} \cong \overline {P'Q'}</math>
 +
| folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend)
 +
|-
 +
| 5. <math>\triangle {ZPQ} \cong \triangle {ZP'Q'}</math>
 +
| sss, folgt aus den Schritten 2-4
 +
|-
 +
| 6. <math>\alpha \cong \alpha'</math><br /> <math>|\alpha|= |\alpha'|</math>
 +
| folgt aus Schritt 5
 +
|-
 +
| 7.<math>|\beta'|=|\alpha'|+|\beta|-|\alpha|</math><br /> <math>|\beta'|=|\beta|</math><br /> <math> \beta' \cong \beta</math>
 +
| rechnen in den reellen Zahlen, Schritt 6
 +
|}<br />--[[Benutzer:Andreas|Andreas]] 15:13, 11. Nov. 2010 (UTC)

Aktuelle Version vom 17. Juli 2013, 18:19 Uhr

  • Weinberge und ihre Parallelität.JPG
  • Geometrie Kugel Andreas.JPG

Spiegelung_Test
Prinzip des Cavalieri und Volumen Kugel

Inhaltsverzeichnis

Satz: Jede Drehung 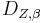D_{Z,\beta} ist eine Bewegung.


Beweis

Voraussetzung: Drehung D um Punkt Z mit dem Winkel \beta
Behauptung: |PQ|=|P'Q'|

Beweisschritt Begründung
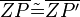
1) \overline {ZP} \tilde = \overline {ZP'} folgt unmittelbar aus der Definition: (Drehung)
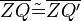
2) \overline {ZQ} \tilde = \overline {ZQ'} folgt unmittelbar aus der Definition: (Drehung)
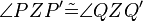
3) \angle {PZP'} \tilde = \angle {QZQ'} folgt unmittelbar aus der Definition: (Drehung)
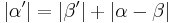
4) |\alpha'|=|\beta'|+|\alpha - \beta|

|\alpha'|= |\alpha|

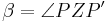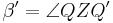
 rechnen in den reellen Zahlen, folgt aus Schritt 3, da \beta = \angle {PZP'} und \beta' = \angle {QZQ'}
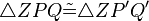
5) \triangle {ZPQ} \tilde = \triangle {ZP'Q'} folgt aus den Schritten 1-4, sws
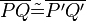
6) \overline {PQ} \tilde = \overline {P'Q'} folgt aus Schritt 5
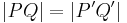
7) |PQ|=|P'Q'| folgt aus Schritt 6, q.e.d

--Andreas 14:22, 9. Nov. 2010 (UTC)

Satz: Wenn eine Bewegung \phi genau einen Fixpunkt Z hat, dann ist \phi eine Drehung um den Fixpunkt Z.

Beweis

Voraussetzung: \phi ist eine Bewegung, \phi hat genau eine Fixpunkt Z
Behauptung: 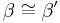\beta \cong \beta'

Beweisschritt Begründung
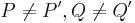
1. P \ne P', Q \ne Q' folgt unmittelbar aus der Voraussetzung (genau ein Fixpunkt Z)
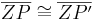
2. \overline {ZP} \cong \overline {ZP'} folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend)
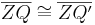
3. \overline {ZQ} \cong \overline {ZQ'} folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend)
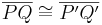
4. \overline {PQ} \cong \overline {P'Q'} folgt unmittelbar aus der Voraussetzung bzw. der Def. Bewegung (Bewegung ist abstandserhaltend)
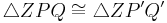
5. \triangle {ZPQ} \cong \triangle {ZP'Q'} sss, folgt aus den Schritten 2-4
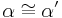6. \alpha \cong \alpha'
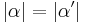
|\alpha|= |\alpha'| 		folgt aus Schritt 5
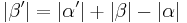7.|\beta'|=|\alpha'|+|\beta|-|\alpha|
|\beta'|=|\beta|
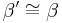
\beta' \cong \beta 		rechnen in den reellen Zahlen, Schritt 6

--Andreas 15:13, 11. Nov. 2010 (UTC)
Von „http://geometrie.zum.de/index.php?title=Benutzer:Andreas&oldid=24814“