Vektorraeume: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=Definition des Begriff des Vektorraums= Eine nicht leere Menge V zusammen mit einer inneren Verknüpfung <math>+: V \times V \to V</math>, <math>(v,v)\map…“) |
(→Definition des Begriff des Vektorraums) |
||
| Zeile 25: | Zeile 25: | ||
S3: Für beliebige <math>u,v \in V</math> und beliebige <math>\lambda \in \mathbb{R} </math> gilt: <math>\lambda \cdot (u+v)=\lambda \cdot u +\lambda \cdot v </math> (1.Distributivgesetz) | S3: Für beliebige <math>u,v \in V</math> und beliebige <math>\lambda \in \mathbb{R} </math> gilt: <math>\lambda \cdot (u+v)=\lambda \cdot u +\lambda \cdot v </math> (1.Distributivgesetz) | ||
| − | S4: Für beliebige <math>v \in V</math> und beliebige <math>\lambda, \mu \in \mathbb{R} </math> gilt: <math>(\lambda + \mu)\cdot u=\lambda \cdot u + \mu \cdot u</math> (2.Distributivgesetz) | + | S4: Für beliebige <math>v \in V</math> und beliebige <math>\lambda, \mu \in \mathbb{R} </math> gilt: <math>(\lambda + \mu)\cdot u=\lambda \cdot u + \mu \cdot u</math> (2.Distributivgesetz)<br /><br /> |
| + | |||
| + | (Weil in der Vorlesung danach gefragt wurden und ich es nicht beantworten konnte: das "S" steht für Skalarmultiplikation ;-) --[[Benutzer:Cplicht|Cplicht]] 18:11, 27. Mai 2013 (CEST) ) | ||
Aktuelle Version vom 27. Mai 2013, 17:11 Uhr
Definition des Begriff des Vektorraums
Eine nicht leere Menge V zusammen mit einer inneren Verknüpfung
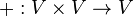 ,
, 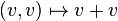
und der äußeren Verknüpfung
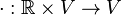 ,
, 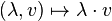
heißt reeler Verktorraum, falls folgende Bedingungen erfüllt sind:
A1: Für beliebige 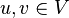 gilt
gilt 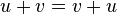 (Kommuntativität der Addition).
(Kommuntativität der Addition).
A2: Für beliebige 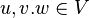 gilt
gilt 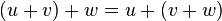 . (Assoziativität der Addition)
. (Assoziativität der Addition)
A3: Es gibt ein neutrales Element 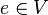 , mit dem für alle Elemente
, mit dem für alle Elemente 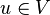 gilt:
gilt: 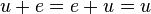 . (Existenz eines neutralen Elements/Nullvektor)
. (Existenz eines neutralen Elements/Nullvektor)
A4: Zu jeden 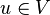 existiert ein Gegenvektor
existiert ein Gegenvektor 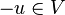 mit
mit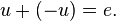
S1: Für beliebige 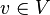 gilt
gilt 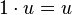 .
.
S2: Für beliebige 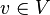 und beliebige
und beliebige 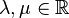 gilt:
gilt: 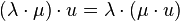 (Assoziativität der Multiplikation von Vektoren mit reelen Zahlen)
(Assoziativität der Multiplikation von Vektoren mit reelen Zahlen)
S3: Für beliebige 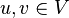 und beliebige
und beliebige 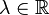 gilt:
gilt: 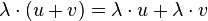 (1.Distributivgesetz)
(1.Distributivgesetz)
S4: Für beliebige 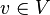 und beliebige
und beliebige 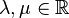 gilt:
gilt: 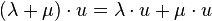 (2.Distributivgesetz)
(2.Distributivgesetz)
(Weil in der Vorlesung danach gefragt wurden und ich es nicht beantworten konnte: das "S" steht für Skalarmultiplikation ;-) --Cplicht 18:11, 27. Mai 2013 (CEST) )

