Vektorraeume

Definition des Begriff des Vektorraums

Eine nicht leere Menge V zusammen mit einer inneren Verknüpfung

$+:V\times V\to V$, $(v,v)\mapsto v+v$

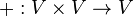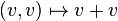
und der äußeren Verknüpfung

$\cdot :\mathbb{ℝ}\times V\to V$, $(\lambda ,v)\mapsto \lambda \cdot v$

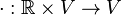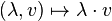
heißt reeler Verktorraum, falls folgende Bedingungen erfüllt sind:

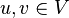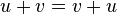A1: Für beliebige $u,v\in V$ gilt $u+v=v+u$ (Kommuntativität der Addition).

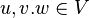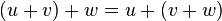A2: Für beliebige $u,v.w\in V$ gilt $(u+v)+w=u+(v+w)$. (Assoziativität der Addition)

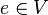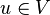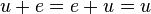A3: Es gibt ein neutrales Element $e\in V$, mit dem für alle Elemente $u\in V$ gilt: $u+e=e+u=u$. (Existenz eines neutralen Elements/Nullvektor)

A4: Zu jeden 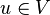$u\in V$ existiert ein Gegenvektor 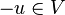$-u\in V$ mit$u+(-u)=e.$

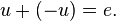
S1: Für beliebige 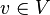$v\in V$ gilt $1\cdot u=u$.

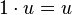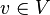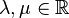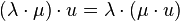S2: Für beliebige $v\in V$ und beliebige $\lambda ,\mu \in \mathbb{ℝ}$ gilt: $(\lambda \cdot \mu )\cdot u=\lambda \cdot (\mu \cdot u)$ (Assoziativität der Multiplikation von Vektoren mit reelen Zahlen)

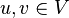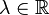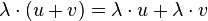S3: Für beliebige $u,v\in V$ und beliebige $\lambda \in \mathbb{ℝ}$ gilt: $\lambda \cdot (u+v)=\lambda \cdot u+\lambda \cdot v$ (1.Distributivgesetz)

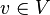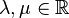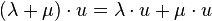S4: Für beliebige $v\in V$ und beliebige $\lambda ,\mu \in \mathbb{ℝ}$ gilt: $(\lambda +\mu )\cdot u=\lambda \cdot u+\mu \cdot u$ (2.Distributivgesetz)

(Weil in der Vorlesung danach gefragt wurden und ich es nicht beantworten konnte: das "S" steht für Skalarmultiplikation ;-) --Cplicht 18:11, 27. Mai 2013 (CEST) )