Lösung von Aufgabe 5.04 S SoSe 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Bemerkung --*m.g.* 23:12, 28. Mai 2013 (CEST)) |
Illu13 (Diskussion | Beiträge) (→Lösung User --Illu13 22:32, 30. Mai 2013 (CEST)) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 45: | Zeile 45: | ||
6. Folgefehler, da 5. nicht korrekt gelöst. | 6. Folgefehler, da 5. nicht korrekt gelöst. | ||
| − | ==Lösung User ...== | + | ==Lösung User --[[Benutzer:Illu13|Illu13]] 22:40, 30. Mai 2013 (CEST)== |
| + | |||
| + | <u>zu 2.</u> | ||
| + | |||
| + | Annahme: Drei Punkte A,B,C sind nicht paarweise verschieden. | ||
| + | |||
| + | <math>\Rightarrow</math> <math>\ A = B \vee A = C \vee B = C </math> | ||
| + | |||
| + | 1. Fall: A = B = C trivial. | ||
| + | |||
| + | 2. Fall: nur zwei der drei Punkte sind identisch (o.B.d.A. A = B <math>\neq</math> C) | ||
| + | |||
| + | <math>\Rightarrow</math> (Axiom I/2) <math>\exists</math>Gerade g: A <math>\in</math> g <math>\wedge</math> C <math>\in</math> g (Gerade {A,C}) und <math>\exists</math>Gerade h: B <math>\in</math> h <math>\wedge</math> C <math>\in</math> h (Gerade {B,C}) | ||
| + | |||
| + | Da wir A = B angenommen haben, folgt daraus g = h. <math>\Rightarrow</math> koll(A,B,C) <math>\Rightarrow</math> Widerspruch zur Voraussetzung. q.e.d. | ||
| + | |||
| + | |||
| + | <u>zu 4.</u> | ||
| + | |||
| + | Annahme: Drei Punkte A,B,C sind paarweise verschieden. | ||
| + | |||
| + | <math>\Rightarrow</math> (Axiom I/3) Die Punkte A,B,C indizieren nicht gemeinsam mit der selben Geraden. | ||
| + | |||
| + | <math>\Rightarrow</math> nkoll(A,B,C), was ein Widerspruch zur Voraussetzung ist. | ||
| + | |||
| + | |||
| + | <u>zu 5.</u> | ||
| + | |||
| + | Wenn drei Punkte paarweise verschieden sind, dann sind sie nicht kollinear. | ||
| + | |||
| + | |||
| + | <u>zu 6.</u> | ||
| + | |||
| + | Stimmt nicht, da alle Punkte auf derselben Geraden liegen könnten. (Dies wäre übrigens ein Sonderfall für den Beweis oben (s.4.).) | ||
| + | |||
| + | --[[Benutzer:Illu13|Illu13]] 22:40, 30. Mai 2013 (CEST) | ||
==Lösung User ...== | ==Lösung User ...== | ||
Aktuelle Version vom 30. Mai 2013, 21:40 Uhr
Aufgabe 5.04Satz I: Je drei nicht kollineare Punkte sind paarweise verschieden.
Lösung User --Userin24 20:37, 28. Mai 2013 (CEST)1. Es seien A, B und C drei Punkte. Wenn A, B und C nicht kollinear sind, dann sind sie paarweise verschieden. 2. Annahme: A, B und C sind nicht paarweise verschieden Annahme impliziert: mind. 2 Punkte sind identisch Widerspruch zur Voraussetzung, dass A, B und C kollinear sind 3. Wenn A, B und C kollinear sind, dann sind sie nicht paarweise verschieden. 4. koll(A, B, C) impliziert: es gibt eine Gerade g, mit der alle drei Punkte inzidieren A, B und C sind deshalb nicht paarweise verschieden. 5. A, B und C sind paarweise verschieden, wenn sie nicht kollinear sind. 6. Ja --Userin24 20:37, 28. Mai 2013 (CEST) Bemerkung --*m.g.* 23:12, 28. Mai 2013 (CEST)1. korrekt Lösung User --Illu13 22:40, 30. Mai 2013 (CEST)zu 2. Annahme: Drei Punkte A,B,C sind nicht paarweise verschieden.
1. Fall: A = B = C trivial. 2. Fall: nur zwei der drei Punkte sind identisch (o.B.d.A. A = B
Da wir A = B angenommen haben, folgt daraus g = h.
Annahme: Drei Punkte A,B,C sind paarweise verschieden.
Wenn drei Punkte paarweise verschieden sind, dann sind sie nicht kollinear.
Stimmt nicht, da alle Punkte auf derselben Geraden liegen könnten. (Dies wäre übrigens ein Sonderfall für den Beweis oben (s.4.).) --Illu13 22:40, 30. Mai 2013 (CEST) Lösung User ...zurück zu Serie 5 SoSe 2013 |
 ,
,  und
und  drei Punkte.“ Ergänzen Sie: „Wenn
drei Punkte.“ Ergänzen Sie: „Wenn 
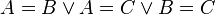
 C)
C)
 Gerade g: A
Gerade g: A  g
g  C
C 
