Lösung von Aufgabe 10.2P (SoSe 13): Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /><br /> | ::In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.<br /><br /> | ||
| − | + | ==Beweisversuch 1== | |
Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:34, 2. Jul. 2013 (CEST):<br /> | Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:34, 2. Jul. 2013 (CEST):<br /> | ||
| Zeile 30: | Zeile 30: | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math>B=S_{m}(A)</math> | | <math>B=S_{m}(A)</math> | ||
| − | | Streckentreue bzw Abstanderhaltung der Geradenspiegelung --[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:48, 2. Jul. 2013 (CEST)<br /> | + | | (2); Streckentreue bzw Abstanderhaltung der Geradenspiegelung --[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:48, 2. Jul. 2013 (CEST)<br /> |
|- | |- | ||
| (4) | | (4) | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math>C=S_{m}(C)</math> | | <math>C=S_{m}(C)</math> | ||
| − | | C∈m mit m:= | + | | (2); C∈m mit m:= Fixpunktgerade⇒ C ist Fixpunkt--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:51, 2. Jul. 2013 (CEST)<br /> |
|- | |- | ||
| (5) | | (5) | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math>M=S_{m}(M)</math> | | <math>M=S_{m}(M)</math> | ||
| − | | M∈m mit m:= | + | | (2); M∈m mit m:= Fixpunktgerade ⇒ M ist Fixpunkt--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:53, 2. Jul. 2013 (CEST)<br /> |
|- | |- | ||
| (6a) | | (6a) | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math> S_{m} (\angle MAC ) = \angle MBC </math> | | <math> S_{m} (\angle MAC ) = \angle MBC </math> | ||
| − | | Winkeltreue der Geradenspiegelung--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:57, 2. Jul. 2013 (CEST)<br /> | + | | (2); (3); (4); (5); Winkeltreue der Geradenspiegelung--[[Benutzer:Nolessonlearned|Nolessonlearned]] 12:57, 2. Jul. 2013 (CEST)<br /> |
|- | |- | ||
|- | |- | ||
| Zeile 51: | Zeile 51: | ||
| <br /><br /><br /> | | <br /><br /><br /> | ||
| <math>\angle MAC \tilde {=} \angle MBC </math> | | <math>\angle MAC \tilde {=} \angle MBC </math> | ||
| − | | .. | + | | (6); Winkelkongruenz der Geradenspiegelung--[[Benutzer:Nolessonlearned|Nolessonlearned]] 17:08, 11. Jul. 2013 (CEST) |
|- | |- | ||
|} | |} | ||
| Zeile 57: | Zeile 57: | ||
Guter Beitrag, Nolessonlearnd! Einige Begründungen sind noch zu ergänzen: | Guter Beitrag, Nolessonlearnd! Einige Begründungen sind noch zu ergänzen: | ||
* Jeder Schritt sollte irgendwo auftauchen, damit er auch ein Recht hat, nicht weggelassen werden zu können. Ergänzt die Nummern! | * Jeder Schritt sollte irgendwo auftauchen, damit er auch ein Recht hat, nicht weggelassen werden zu können. Ergänzt die Nummern! | ||
| − | * Begründung zu Schritt 1 sollte noch ergänzt werden | + | * Begründung zu Schritt 1 sollte noch ergänzt werden - muss nicht, ich würde noch Def. gleichschenkliges Dreieck schreiben --[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:10, 12. Jul. 2013 (CEST) |
* Begründung Schritt 6 ist komplexer. Damit das klarer ist, habe ich deshalb noch ein Zwischenschritt eingefügt. Die Begründungen müssen noch ergänzt werden.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:01, 2. Jul. 2013 (CEST) | * Begründung Schritt 6 ist komplexer. Damit das klarer ist, habe ich deshalb noch ein Zwischenschritt eingefügt. Die Begründungen müssen noch ergänzt werden.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 18:01, 2. Jul. 2013 (CEST) | ||
| + | * Danke Nolessonlearnd für das richtige Ergänzen. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:10, 12. Jul. 2013 (CEST) | ||
| − | + | ==Versuch2== | |
| − | + | ||
| − | + | ||
| − | + | ||
Ich habe den Beweis selbst versucht: <br /> | Ich habe den Beweis selbst versucht: <br /> | ||
[[Datei:IMG 0002.jpg|| 700px]]--[[Benutzer:Regenschirm|Regenschirm]] 18:00, 2. Jul. 2013 (CEST)<br /> | [[Datei:IMG 0002.jpg|| 700px]]--[[Benutzer:Regenschirm|Regenschirm]] 18:00, 2. Jul. 2013 (CEST)<br /> | ||
Der Beweis ist korrekt. Ich würde die Begründungen für Schritt 1 und 6 noch ergänzen.<br /> | Der Beweis ist korrekt. Ich würde die Begründungen für Schritt 1 und 6 noch ergänzen.<br /> | ||
Allerdings hast du nicht die Abbildungsgeometrie genutzt sondern bist über den Kongruenzsatz SSW gegangen. So wie wir hier die Geometrie aufbauen (Abbildungsgeometrisch eben), haben wir diese Kongruenzsätze aber noch nicht bewiesen und genau genommen, hast du die Aufgabe damit nicht erfüllt (da nicht abbildungsgeometrisch bewiesen).--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:37, 3. Jul. 2013 (CEST) | Allerdings hast du nicht die Abbildungsgeometrie genutzt sondern bist über den Kongruenzsatz SSW gegangen. So wie wir hier die Geometrie aufbauen (Abbildungsgeometrisch eben), haben wir diese Kongruenzsätze aber noch nicht bewiesen und genau genommen, hast du die Aufgabe damit nicht erfüllt (da nicht abbildungsgeometrisch bewiesen).--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:37, 3. Jul. 2013 (CEST) | ||
| + | ==Was muss ich mir konkret unter abbildungsgeometrischen Beweismethoden vorstellen?== | ||
| + | --[[Benutzer:Nolessonlearned|Nolessonlearned]] 17:13, 12. Jul. 2013 (CEST)<br /> | ||
| + | Abbildungsgeometrisch heißt, dass zwei Dinge dann kongruent sind, wenn sie aufeinander abgebildet werden können (durch Drehung, Spiegelung etc. ).<br /> | ||
| + | Kongruenzgeometrie besagt, dass zwei Dinge kongruent sind, wenn sie gleiche Eigenschaften haben (z.B. Winkelmaß, Seitenlänge etc.).<br /> | ||
| + | |||
| + | Beispiel: Winkelkongruenz bedeutet, zwei Winkel haben das selbe Maß (Def. in der Kongruenzgeometrie).<br /> | ||
| + | Zwei Winkel sind kongruent, wenn es eine Abbildung gibt, die den einen Winkel auf den anderen abbilden lässt. (Def.in Abbildungsgeometrie)<br /> | ||
| + | |||
| + | Wenn man genau hinschaut, seid ihr in der Vorlesung ähnlich wie in der Schule vorgegangen (Kongruenzgeometrisch) und dann in die Abbildungsgeometrie gewechselt, weil sie viel anschaulicher ist. <br /> | ||
| + | Ich hoffe, dass ich das nun richtig und verständlich erklärt habe.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 17:50, 12. Jul. 2013 (CEST) | ||
| + | **Vielen Dank. Super Erklärung.--[[Benutzer:Nolessonlearned|Nolessonlearned]] 22:23, 12. Jul. 2013 (CEST) | ||
Aktuelle Version vom 12. Juli 2013, 21:23 Uhr
Beweisen Sie mit abbildungsgeometrischen Mitteln den Basiswinkelsatz.
Inhaltsverzeichnis |
Satz VIII.1: (Basiswinkelsatz)
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
- In jedem gleichschenkligen Dreieck sind die Basiswinkel kongruent zueinander.
Beweisversuch 1
Voraussetzung: Das Dreieck ist gleichschenklig: |AC| = |BC|--Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
Behauptung: Die Basiswinkel sind kongruent zueinander: |α| = |β| --Nolessonlearned 12:34, 2. Jul. 2013 (CEST):
- Deine Vorausetzung enthält schon Schritt 1. Das ist nicht optimal. Besser ist es, wirklich nur den ersten Teil zu nennen und den 2.Teil wegzulassen. Bei der Behauptung kannst du dir Teil 2 auch sparen, da dieser ja nicht beim Beweis am Ende rauskommt, sondern direkt die Kongruenz da steht. --Tutorin Anne 18:01, 2. Jul. 2013 (CEST)
| Nr. | Skizze | Beweisschritt | Begründung |
|---|---|---|---|
| (1) | 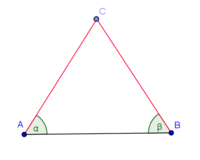
|
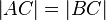
|
Voraussetzung --Nolessonlearned 12:36, 2. Jul. 2013 (CEST) |
| (2) | 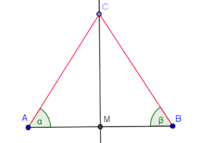
|
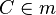 mit mit  ist Mittelsenkrechte von ist Mittelsenkrechte von 
|
(1); Mittelsenkrechtenkriterium --Nolessonlearned 12:37, 2. Jul. 2013 (CEST) |
| (3) | |
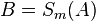
|
(2); Streckentreue bzw Abstanderhaltung der Geradenspiegelung --Nolessonlearned 12:48, 2. Jul. 2013 (CEST) |
| (4) | |
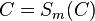
|
(2); C∈m mit m:= Fixpunktgerade⇒ C ist Fixpunkt--Nolessonlearned 12:51, 2. Jul. 2013 (CEST) |
| (5) | |
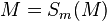
|
(2); M∈m mit m:= Fixpunktgerade ⇒ M ist Fixpunkt--Nolessonlearned 12:53, 2. Jul. 2013 (CEST) |
| (6a) | |
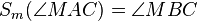
|
(2); (3); (4); (5); Winkeltreue der Geradenspiegelung--Nolessonlearned 12:57, 2. Jul. 2013 (CEST) |
| (6b) | |
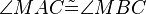
|
(6); Winkelkongruenz der Geradenspiegelung--Nolessonlearned 17:08, 11. Jul. 2013 (CEST) |
Guter Beitrag, Nolessonlearnd! Einige Begründungen sind noch zu ergänzen:
- Jeder Schritt sollte irgendwo auftauchen, damit er auch ein Recht hat, nicht weggelassen werden zu können. Ergänzt die Nummern!
- Begründung zu Schritt 1 sollte noch ergänzt werden - muss nicht, ich würde noch Def. gleichschenkliges Dreieck schreiben --Tutorin Anne 17:10, 12. Jul. 2013 (CEST)
- Begründung Schritt 6 ist komplexer. Damit das klarer ist, habe ich deshalb noch ein Zwischenschritt eingefügt. Die Begründungen müssen noch ergänzt werden.--Tutorin Anne 18:01, 2. Jul. 2013 (CEST)
- Danke Nolessonlearnd für das richtige Ergänzen. --Tutorin Anne 17:10, 12. Jul. 2013 (CEST)
Versuch2
Ich habe den Beweis selbst versucht:
 --Regenschirm 18:00, 2. Jul. 2013 (CEST)
--Regenschirm 18:00, 2. Jul. 2013 (CEST)
Der Beweis ist korrekt. Ich würde die Begründungen für Schritt 1 und 6 noch ergänzen.
Allerdings hast du nicht die Abbildungsgeometrie genutzt sondern bist über den Kongruenzsatz SSW gegangen. So wie wir hier die Geometrie aufbauen (Abbildungsgeometrisch eben), haben wir diese Kongruenzsätze aber noch nicht bewiesen und genau genommen, hast du die Aufgabe damit nicht erfüllt (da nicht abbildungsgeometrisch bewiesen).--Tutorin Anne 10:37, 3. Jul. 2013 (CEST)
Was muss ich mir konkret unter abbildungsgeometrischen Beweismethoden vorstellen?
--Nolessonlearned 17:13, 12. Jul. 2013 (CEST)
Abbildungsgeometrisch heißt, dass zwei Dinge dann kongruent sind, wenn sie aufeinander abgebildet werden können (durch Drehung, Spiegelung etc. ).
Kongruenzgeometrie besagt, dass zwei Dinge kongruent sind, wenn sie gleiche Eigenschaften haben (z.B. Winkelmaß, Seitenlänge etc.).
Beispiel: Winkelkongruenz bedeutet, zwei Winkel haben das selbe Maß (Def. in der Kongruenzgeometrie).
Zwei Winkel sind kongruent, wenn es eine Abbildung gibt, die den einen Winkel auf den anderen abbilden lässt. (Def.in Abbildungsgeometrie)
Wenn man genau hinschaut, seid ihr in der Vorlesung ähnlich wie in der Schule vorgegangen (Kongruenzgeometrisch) und dann in die Abbildungsgeometrie gewechselt, weil sie viel anschaulicher ist.
Ich hoffe, dass ich das nun richtig und verständlich erklärt habe.--Tutorin Anne 17:50, 12. Jul. 2013 (CEST)
- Vielen Dank. Super Erklärung.--Nolessonlearned 22:23, 12. Jul. 2013 (CEST)

