Lösung von Aufgabe 4.3 P (SoSe 13): Unterschied zwischen den Versionen
| Zeile 42: | Zeile 42: | ||
Wenn eine Gerade senkrecht auf einer Strecke steht und die Anfangspunkte der Strecke zu jedem Punkt der Geraden ein und den selben Abstand haben, dann nennt man diese Gerade Mittelsenkrechte der Strecke.<br />--[[Benutzer:Wüstenfuchs|Wüstenfuchs]] 17:38, 5. Jul. 2013 (CEST)<br /> | Wenn eine Gerade senkrecht auf einer Strecke steht und die Anfangspunkte der Strecke zu jedem Punkt der Geraden ein und den selben Abstand haben, dann nennt man diese Gerade Mittelsenkrechte der Strecke.<br />--[[Benutzer:Wüstenfuchs|Wüstenfuchs]] 17:38, 5. Jul. 2013 (CEST)<br /> | ||
Wenn eine Punktmenge genau alle Punkte enthält, die zu den Anfangspunkten einer Strecke ein und den selben Abstand haben, so nennt man diese Punktmenge auch Mittelsenkrechte dieser Strecke.<br /> | Wenn eine Punktmenge genau alle Punkte enthält, die zu den Anfangspunkten einer Strecke ein und den selben Abstand haben, so nennt man diese Punktmenge auch Mittelsenkrechte dieser Strecke.<br /> | ||
| − | --[[Benutzer:Wüstenfuchs|Wüstenfuchs]] 17:55, 5. Jul. 2013 (CEST) | + | --[[Benutzer:Wüstenfuchs|Wüstenfuchs]] 17:55, 5. Jul. 2013 (CEST)<br /> |
| + | OK. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:27, 8. Jul. 2013 (CEST) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
Aktuelle Version vom 8. Juli 2013, 13:27 Uhr
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
- Wenn eine Gerade m eine Strecke
 mit folgender Bedingung schneidet P ∈ m ∧ P:= { P | |AP| ≌ |BP|}, dann ist m die Mittelsenkrechte der Strecke
mit folgender Bedingung schneidet P ∈ m ∧ P:= { P | |AP| ≌ |BP|}, dann ist m die Mittelsenkrechte der Strecke  .--Nolessonlearned 17:07, 14. Mai 2013 (CEST)
.--Nolessonlearned 17:07, 14. Mai 2013 (CEST)
- Gute Idee und fast richtig. Allerdings noch nicht exakt genug. Einmal nutzt du P als Punkt und einmal als Menge, oder? Und zudem gibt es viele Geraden bezüglich einer Strecke, auf denen ein Punkt liegt, der den selben Abstand zu den Endpunkten dieser Strecke hat.--Tutorin Anne 15:00, 15. Mai 2013 (CEST)
- Gute Idee und fast richtig. Allerdings noch nicht exakt genug. Einmal nutzt du P als Punkt und einmal als Menge, oder? Und zudem gibt es viele Geraden bezüglich einer Strecke, auf denen ein Punkt liegt, der den selben Abstand zu den Endpunkten dieser Strecke hat.--Tutorin Anne 15:00, 15. Mai 2013 (CEST)
- Wenn eine Gerade m und die Strecke
 sich innerhalb der selben Ebene befinden und sich mit folgender Bedingung schneiden
sich innerhalb der selben Ebene befinden und sich mit folgender Bedingung schneiden
∃ Q mit Q := { m ∩ A͞B } ∧ m:= { P | |AP| ≌ |BP|}, dann ist m die Mittelsenkrechte der Strecke .--Nolessonlearned 12:32, 16. Mai 2013 (CEST)
.--Nolessonlearned 12:32, 16. Mai 2013 (CEST)
- Die erste Bedingung ∃ Q mit Q := { m ∩ A͞B } brauchst du nicht, da sie in der zweiten enthalten ist. --Tutorin Anne 19:50, 22. Mai 2013 (CEST)
- Wenn die Menge aller Punkte von zwei gegebenen Punkten A und B denselben Abstand haben, dann ist es eine Mittelsenkrechte.
- Hier hast du vergessen die Strecke zu erwähnen, die von den Punkten A und B begrenzt wird. Eine Mittelsenkrechte existiert nur in Relation zu einer Strecke. --Nolessonlearned 11:49, 15. Mai 2013 (CEST)
- Richtig. Zudem kann eine Menge nicht einen Abstand haben. Es muss also noch weiter korrigiert werden. Dies gilt auch für die darauffolgende Definition.--Tutorin Anne 15:00, 15. Mai 2013 (CEST)
- Richtig. Zudem kann eine Menge nicht einen Abstand haben. Es muss also noch weiter korrigiert werden. Dies gilt auch für die darauffolgende Definition.--Tutorin Anne 15:00, 15. Mai 2013 (CEST)
- Hier hast du vergessen die Strecke zu erwähnen, die von den Punkten A und B begrenzt wird. Eine Mittelsenkrechte existiert nur in Relation zu einer Strecke. --Nolessonlearned 11:49, 15. Mai 2013 (CEST)
- Wenn eine Punktmenge zu den Endpunkten der Strecke
 einen identischen Abstand hat, dann ist diese Punktmenge die Mittelsenkrechte der Strecke
einen identischen Abstand hat, dann ist diese Punktmenge die Mittelsenkrechte der Strecke  .--Nolessonlearned 11:40, 15. Mai 2013 (CEST)
.--Nolessonlearned 11:40, 15. Mai 2013 (CEST)
- Wenn eine Gerade m zu den Punkten A und B der Strecke
 einen identischen Abstand hat, dann ist diese Gerade die Mittelsenkrechte der Strecke
einen identischen Abstand hat, dann ist diese Gerade die Mittelsenkrechte der Strecke  .--Nolessonlearned 12:38, 16. Mai 2013 (CEST)
.--Nolessonlearned 12:38, 16. Mai 2013 (CEST)
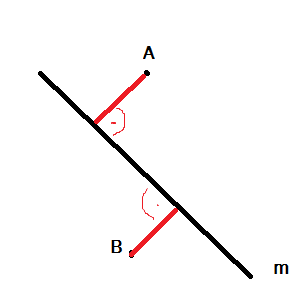
Hier erkennst du, dass die Definition so nicht korrekt ist.--Tutorin Anne 10:35, 23. Mai 2013 (CEST)
- Wenn eine Gerade senkrecht zu einer Strecke verläuft und diese in der hälfte teilt, dann ist es eine Mittelsenkrecht.--Regenschirm 21:28, 14. Mai 2013 (CEST)
- Hierbei müssten wahrscheinlich die Begriffe "senkrecht" und "Hälfte" erst definiert werden.--Nolessonlearned 11:49, 15. Mai 2013 (CEST)
- senkrecht zur Strecke steht - kann man verwenden. Das ist eine mathematische Relation. "Hälfte" müsste man definitiv genauer beschreiben. Besser ist es auf den Begriff "Mittelpunkt" zurückzugreifen.--Tutorin Anne 15:00, 15. Mai 2013 (CEST)
- Hierbei müssten wahrscheinlich die Begriffe "senkrecht" und "Hälfte" erst definiert werden.--Nolessonlearned 11:49, 15. Mai 2013 (CEST)
Ich bin etwas irritiert, was jetzt die RICHTIGE LÖSUNG ist.??;-//
Bei Definitionen gibt es nicht die eine richtige Lösung!--Tutorin Anne 13:11, 29. Mai 2013 (CEST)
Meine Definitionen lauten wie folgt:
- Wenn alle Punkte einer Ebene die zu den Endpunkten A, B einer Strecke AB jeweils ein und denselben Abstand haben gehören sie sie zur Mittelsenkrechten m der Strecke AB.
- Dann könnte es ja auch andere Punkte geben, die zur Mittelsenkrechte gehören, oder? Ich meine, das ist noch nicht korrekt.--Tutorin Anne 13:11, 29. Mai 2013 (CEST)
- Wenn alle Punkte die zu einer Mittelsenkrechten der Strecke AB gehören, haben die Punkte A und B jeweils ein und denselben Abstand. --Blumenkind 16:56, 27. Mai 2013 (CEST)Blumenkind 27. Mai 16:56
- Wenn du die beiden Definitionsversuche zusammen nimmst, dann könnte es eine richtige Definition werden. Diese beiden Definitionen sind so nicht korrekt und nicht prinzipiell verschieden.--Tutorin Anne 13:11, 29. Mai 2013 (CEST)
- Wenn ich beide Sätze zusammen verbinde dann bekomme ich : Es ist aber keine Konventialdefinition sondern eine Realdefinition. Kannst du mir bitte weiterhelfen, ich komm nicht mehr weiter. --Blumenkind 16:19, 3. Jun. 2013 (CEST)Blumenkind 16:19, 3. Juni
- Die Mittelsenkrechte einer Strecke
 ist die Menge genau aller Punkte, die zu A und B jeweils ein und denselben Abstand hat. - so wäre es erstmal korrekt. Wir schauen mal darüber hinweg, dass Mengen eigentlich ja kein Abstand haben können. Diese jetzt in eine Konvenzionaldefinition umzuwandeln, dürfte nicht mehr schwer sein. --Tutorin Anne 20:00, 5. Jun. 2013 (CEST)
ist die Menge genau aller Punkte, die zu A und B jeweils ein und denselben Abstand hat. - so wäre es erstmal korrekt. Wir schauen mal darüber hinweg, dass Mengen eigentlich ja kein Abstand haben können. Diese jetzt in eine Konvenzionaldefinition umzuwandeln, dürfte nicht mehr schwer sein. --Tutorin Anne 20:00, 5. Jun. 2013 (CEST)
- Wenn eine Punktemenge genau alle Punkte enthält, ...
- Wenn eine Punktemenge genau alle Punkte enthält, ...
- Die Mittelsenkrechte einer Strecke
- Wenn ich beide Sätze zusammen verbinde dann bekomme ich : Es ist aber keine Konventialdefinition sondern eine Realdefinition. Kannst du mir bitte weiterhelfen, ich komm nicht mehr weiter. --Blumenkind 16:19, 3. Jun. 2013 (CEST)Blumenkind 16:19, 3. Juni
- Wenn du die beiden Definitionsversuche zusammen nimmst, dann könnte es eine richtige Definition werden. Diese beiden Definitionen sind so nicht korrekt und nicht prinzipiell verschieden.--Tutorin Anne 13:11, 29. Mai 2013 (CEST)
Wenn eine Gerade senkrecht auf einer Strecke steht und die Anfangspunkte der Strecke zu jedem Punkt der Geraden ein und den selben Abstand haben, dann nennt man diese Gerade Mittelsenkrechte der Strecke.
--Wüstenfuchs 17:38, 5. Jul. 2013 (CEST)
Wenn eine Punktmenge genau alle Punkte enthält, die zu den Anfangspunkten einer Strecke ein und den selben Abstand haben, so nennt man diese Punktmenge auch Mittelsenkrechte dieser Strecke.
--Wüstenfuchs 17:55, 5. Jul. 2013 (CEST)
OK. --Tutorin Anne 14:27, 8. Jul. 2013 (CEST)

