Lösung von Aufg. 12.03 SoSe 13: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Lösung) |
*m.g.* (Diskussion | Beiträge) (→Lösung) |
||
| Zeile 9: | Zeile 9: | ||
Annahme: <math>t</math> ist nicht Tangente an <math>k</math>. <br /> | Annahme: <math>t</math> ist nicht Tangente an <math>k</math>. <br /> | ||
| − | Da <math>t</math> nach Voraussetzung den Punkt <math>B</math> mit <math>k</math> gemeinsam hat, bedeutet unsere Annahme, dass <math>t</math> einen weiteren Punkt <math>A</math> mit <math>k</math> gemeinsam hat. Da <math>\overline{MB}</math> und <math>\overline{MB}</math> jetzt Radien von <math>k</math> sind, ist das Dreieck <math>\overline{MAB}</math> gleichschenklig. Die Basiswinkel <math>\angle MAB</math> und <math>\angle MBA</math> wären demzufolge kongruent zueinander. Nach Voraussetzung ist <math>\angle MBA</math> ein Rechter Winkel. Selbiges gilt für den zu ihm kongruenten Basiswinkel <math>\angle MAB</math>. Das Dreieck <math>\overline{MAB</math> hätte damit zwei Rechte Innenwinkel, was ein Widerspruch zu den Folgerungen aus dem schwachen Außenwinkelsatz ist: In jdem Dreieck gibt es zwei spitze Innenwinkel.--[[Benutzer:*m.g.*|*m.g.*]] 22:09, 18. Jul. 2013 (CEST)<br /> | + | Da <math>t</math> nach Voraussetzung den Punkt <math>B</math> mit <math>k</math> gemeinsam hat, bedeutet unsere Annahme, dass <math>t</math> einen weiteren Punkt <math>A</math> mit <math>k</math> gemeinsam hat. Da <math>\overline{MB}</math> und <math>\overline{MB}</math> jetzt Radien von <math>k</math> sind, ist das Dreieck <math>\overline{MAB}</math> gleichschenklig. Die Basiswinkel <math>\angle MAB</math> und <math>\angle MBA</math> wären demzufolge kongruent zueinander. Nach Voraussetzung ist <math>\angle MBA</math> ein Rechter Winkel. Selbiges gilt für den zu ihm kongruenten Basiswinkel <math>\angle MAB</math>. Das Dreieck <math>\overline{MAB</math> hätte damit zwei Rechte Innenwinkel, was ein Widerspruch zu den Folgerungen aus dem schwachen Außenwinkelsatz ist: In jdem Dreieck gibt es zwei spitze Innenwinkel.--[[Benutzer:*m.g.*|*m.g.*]] 22:09, 18. Jul. 2013 (CEST)<br /><br /><br /><br /> |
Zurück zu: [[Serie 12 SoSe 2013]] | Zurück zu: [[Serie 12 SoSe 2013]] | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 18. Juli 2013, 21:09 Uhr
Aufgabe 12.03Alles in ein und derselben Ebene: LösungAnnahme: hätte damit zwei Rechte Innenwinkel, was ein Widerspruch zu den Folgerungen aus dem schwachen Außenwinkelsatz ist: In jdem Dreieck gibt es zwei spitze Innenwinkel.--*m.g.* 22:09, 18. Jul. 2013 (CEST) Zurück zu: Serie 12 SoSe 2013 |
 ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner seien
. Ferner seien  ein Punkt von
ein Punkt von  eine Gerade durch
eine Gerade durch  steht. Beweisen Sie:
steht. Beweisen Sie:  mit
mit 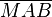 gleichschenklig. Die Basiswinkel
gleichschenklig. Die Basiswinkel 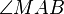 und
und 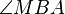 wären demzufolge kongruent zueinander. Nach Voraussetzung ist
wären demzufolge kongruent zueinander. Nach Voraussetzung ist 
