Aufgabe 12.03
Alles in ein und derselben Ebene:
Es sei  ein Kreis mit dem Mittelpunkt ein Kreis mit dem Mittelpunkt  . Ferner seien . Ferner seien  ein Punkt von ein Punkt von  und und  eine Gerade durch eine Gerade durch  , die senkrecht auf , die senkrecht auf  steht. Beweisen Sie: steht. Beweisen Sie:  ist Tangente an ist Tangente an  im Punkt im Punkt  . .
Lösung
Annahme:  ist nicht Tangente an ist nicht Tangente an  . .
Da  nach Voraussetzung den Punkt nach Voraussetzung den Punkt  mit mit  gemeinsam hat, bedeutet unsere Annahme, dass gemeinsam hat, bedeutet unsere Annahme, dass  einen weiteren Punkt einen weiteren Punkt  mit mit  gemeinsam hat. Da gemeinsam hat. Da  und und  jetzt Radien von jetzt Radien von  sind, ist das Dreieck sind, ist das Dreieck 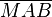 gleichschenklig. Die Basiswinkel gleichschenklig. Die Basiswinkel 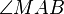 und und 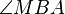 wären demzufolge kongruent zueinander. Nach Voraussetzung ist wären demzufolge kongruent zueinander. Nach Voraussetzung ist  ein Rechter Winkel. Selbiges gilt für den zu ihm kongruenten Basiswinkel ein Rechter Winkel. Selbiges gilt für den zu ihm kongruenten Basiswinkel 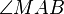 . Das Dreieck Fehler beim Parsen(Syntaxfehler): \overline{MAB . Das Dreieck Fehler beim Parsen(Syntaxfehler): \overline{MAB
hätte damit zwei Rechte Innenwinkel, was ein Widerspruch zu den Folgerungen aus dem schwachen Außenwinkelsatz ist: In jdem Dreieck gibt es zwei spitze Innenwinkel.--*m.g.* 22:09, 18. Jul. 2013 (CEST)
Zurück zu: Serie 12 SoSe 2013
|  ein Kreis mit dem Mittelpunkt
ein Kreis mit dem Mittelpunkt  . Ferner seien
. Ferner seien  ein Punkt von
ein Punkt von  eine Gerade durch
eine Gerade durch  steht. Beweisen Sie:
steht. Beweisen Sie:  mit
mit 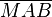 gleichschenklig. Die Basiswinkel
gleichschenklig. Die Basiswinkel 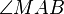 und
und 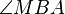 wären demzufolge kongruent zueinander. Nach Voraussetzung ist
wären demzufolge kongruent zueinander. Nach Voraussetzung ist 
