Lösung von Aufgabe 12.3P (WS 13/14): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie Satz IX.9:<br /> Gegeben seien zwei zueinander parallele Spiegelgeraden ''a'' und ''b''. Wir betrachten die Verkettung <math>S_{a}\circ S_{b} </ma…“) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Beweisen Sie Satz IX.9:<br /> | Beweisen Sie Satz IX.9:<br /> | ||
Gegeben seien zwei zueinander parallele Spiegelgeraden ''a'' und ''b''. Wir betrachten die Verkettung <math>S_{a}\circ S_{b} </math>. Jeder Punkt ''P'' hat dabei zu seinem Bildpunkt <math>P''=S_{a}\circ S_{b}(P) </math> einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.<br /> | Gegeben seien zwei zueinander parallele Spiegelgeraden ''a'' und ''b''. Wir betrachten die Verkettung <math>S_{a}\circ S_{b} </math>. Jeder Punkt ''P'' hat dabei zu seinem Bildpunkt <math>P''=S_{a}\circ S_{b}(P) </math> einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.<br /> | ||
| − | [[Kategorie:Einführung_P]] | + | <br> |
| + | <br> | ||
| + | ::(1) <math>S_{a}</math> bildet <math> A </math> auf <math> A' </math> ab und<br> | ||
| + | ::(2) <math>S_{b}</math> bildet <math> A' </math> auf <math> A'' </math> ab. | ||
| + | ::(3) Der Abstand von <math>A</math> zur Spiegelgeraden <math>a</math> ist gleich dem Abstand von <math>A'</math> zu <math>a</math>. | (1); Eig. der Geradenspiegelung;<br> | ||
| + | ::(4) Der Abstand von <math>A'</math> zu <math>b</math> ist gleich dem Abstand von <math>A''</math> zu <math>b</math>. | (2); Eig. der Geradenspiegelung;<br> | ||
| + | ::(5) Der Abstand von <math>a</math> zu <math>b</math> ist somit gleich dem Abstand von <math>A'</math> zu <math>a</math> <math>+</math> dem Abstand von <math>A'</math> zu <math>b</math>. | (3); (4);<br> | ||
| + | ::(6) Das ist Gleich der Summe der Abstände von <math>A</math> zur Spiegelgeraden <math>a</math> <math>+</math> dem Abstand von <math>A''</math> zu <math>b</math> |(3); (4); (5);<br> | ||
| + | ::--[[Benutzer:EarlHickey|EarlHickey]] ([[Benutzer Diskussion:EarlHickey|Diskussion]]) 08:17, 10. Feb. 2014 (CET)<br> | ||
| + | <br> | ||
| + | [[Kategorie:Einführung_P]]<br /> | ||
| + | |||
| + | Ich kann den Beweis nachvollziehen. Allerdings scheint mir hier noch ein Schritt zu fehlen. Was ist denn die Behauptung, die im obrigen Satz steckt? Was muss am Ende genau gezeigt werden? Zu einem korrekten Beweis gehört generell eine Voraussetzung und eine Behauptung zu Beginn, auch wenn dies meist im Satz offensichtlich steht.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 13:40, 10. Feb. 2014 (CET)<br /> | ||
Aktuelle Version vom 10. Februar 2014, 13:40 Uhr
Beweisen Sie Satz IX.9:
Gegeben seien zwei zueinander parallele Spiegelgeraden a und b. Wir betrachten die Verkettung  . Jeder Punkt P hat dabei zu seinem Bildpunkt
. Jeder Punkt P hat dabei zu seinem Bildpunkt  einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.
einen Abstand der doppelt so groß ist wie der Abstand der beiden Spiegelgeraden.
- (1)
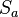 bildet
bildet  auf
auf 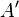 ab und
ab und
- (2)
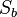 bildet
bildet 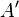 auf
auf 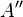 ab.
ab.
- (3) Der Abstand von
 zur Spiegelgeraden
zur Spiegelgeraden  ist gleich dem Abstand von
ist gleich dem Abstand von 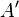 zu
zu  . | (1); Eig. der Geradenspiegelung;
. | (1); Eig. der Geradenspiegelung;
- (4) Der Abstand von
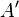 zu
zu  ist gleich dem Abstand von
ist gleich dem Abstand von 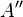 zu
zu  . | (2); Eig. der Geradenspiegelung;
. | (2); Eig. der Geradenspiegelung;
- (5) Der Abstand von
 zu
zu  ist somit gleich dem Abstand von
ist somit gleich dem Abstand von 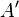 zu
zu 
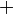 dem Abstand von
dem Abstand von 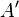 zu
zu  . | (3); (4);
. | (3); (4);
- (6) Das ist Gleich der Summe der Abstände von
 zur Spiegelgeraden
zur Spiegelgeraden 
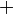 dem Abstand von
dem Abstand von 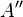 zu
zu  |(3); (4); (5);
|(3); (4); (5);
- --EarlHickey (Diskussion) 08:17, 10. Feb. 2014 (CET)
- (1)
Ich kann den Beweis nachvollziehen. Allerdings scheint mir hier noch ein Schritt zu fehlen. Was ist denn die Behauptung, die im obrigen Satz steckt? Was muss am Ende genau gezeigt werden? Zu einem korrekten Beweis gehört generell eine Voraussetzung und eine Behauptung zu Beginn, auch wenn dies meist im Satz offensichtlich steht.--Tutorin Anne (Diskussion) 13:40, 10. Feb. 2014 (CET)

