Lösung von Aufgabe 5.3 P (SoSe 14): Unterschied zwischen den Versionen
| (6 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br /> | <math>\ g S h \Leftrightarrow \ g \cap h \neq \lbrace \rbrace </math><br /> | ||
| − | Die Relation ist symmetrisch, | + | Die Relation ist symmetrisch, reflexiv und transitiv (Also ein Äquivalenzrelation). --[[Benutzer:MarieSo|MarieSo]] ([[Benutzer Diskussion:MarieSo|Diskussion]]) 19:25, 26. Mai 2014 (CEST) |
| − | + | ||
| + | Richtig --[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 21:23, 26. Mai 2014 (CEST) | ||
[[Category:Einführung_P]] | [[Category:Einführung_P]] | ||
| + | |||
| + | |||
| + | Wisst Ihr das nur wegen dem Leftrightarrow oder weil Ihr Euch das irgendwie mit einer Wahrheitstabelle hergeleitet habt? | ||
| + | Ich verstehe gar nicht, was ich damit anfangen soll... :o( Außer dass der Leftrightarrow = Äquivalenzrelation heißt und diese immer symmetrisch, reflexiv und transitiv ist. | ||
| + | --[[Benutzer:Pippilotta|Pippilotta]] ([[Benutzer Diskussion:Pippilotta|Diskussion]]) 16:47, 27. Mai 2014 (CEST) | ||
| + | |||
| + | |||
| + | Mach dir eine Skizze dazu. Der Satz besagt, dass g schneidet h genau dann, wenn g h schneidet und dabei keine leere Menge ergibt, also ein Schnittpunkt entsteht.<br /> | ||
| + | Reflexiv: jede Gerade schneidet sich selbst<br /> | ||
| + | Symmetrisch: wenn g h schneidet, dann auch h schneidet g.<br /> | ||
| + | Transitiv: dafür nimmst du noch eine Gerade z.B. c. Wenn g schneidet h und h schneidet c, dann muss g auch c schneiden. --[[Benutzer:Picksel|Picksel]] ([[Benutzer Diskussion:Picksel|Diskussion]]) 09:54, 29. Mai 2014 (CEST)<br /> | ||
| + | |||
| + | |||
| + | Danke Picksel, dass hast du schön erklärt. Das Äquilanzzeichen besagt hier einfach, dass die Relation <math>\ g S h </math> so definiert ist.--[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 08:38, 2. Jun. 2014 (CEST) | ||
| + | |||
| + | |||
| + | Aber könnten g und c nicht auch parallel sein? Dann würde h sowohl g als auch c schneiden aber g würde nicht c schneiden.<br /> | ||
| + | |||
| + | Du hast absolut Recht. Die Relation ist damit nicht transitiv, da du dies mit einem Gegenbeispiel belegt hast. --[[Benutzer:Tutorin Anne|Tutorin Anne]] ([[Benutzer Diskussion:Tutorin Anne|Diskussion]]) 16:48, 5. Jun. 2014 (CEST) | ||
Aktuelle Version vom 5. Juni 2014, 15:48 Uhr
Untersuchen Sie folgende Relation S auf ihre Eigenschaften:
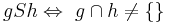
Die Relation ist symmetrisch, reflexiv und transitiv (Also ein Äquivalenzrelation). --MarieSo (Diskussion) 19:25, 26. Mai 2014 (CEST)
Richtig --Picksel (Diskussion) 21:23, 26. Mai 2014 (CEST)
Wisst Ihr das nur wegen dem Leftrightarrow oder weil Ihr Euch das irgendwie mit einer Wahrheitstabelle hergeleitet habt?
Ich verstehe gar nicht, was ich damit anfangen soll... :o( Außer dass der Leftrightarrow = Äquivalenzrelation heißt und diese immer symmetrisch, reflexiv und transitiv ist.
--Pippilotta (Diskussion) 16:47, 27. Mai 2014 (CEST)
Mach dir eine Skizze dazu. Der Satz besagt, dass g schneidet h genau dann, wenn g h schneidet und dabei keine leere Menge ergibt, also ein Schnittpunkt entsteht.
Reflexiv: jede Gerade schneidet sich selbst
Symmetrisch: wenn g h schneidet, dann auch h schneidet g.
Transitiv: dafür nimmst du noch eine Gerade z.B. c. Wenn g schneidet h und h schneidet c, dann muss g auch c schneiden. --Picksel (Diskussion) 09:54, 29. Mai 2014 (CEST)
Danke Picksel, dass hast du schön erklärt. Das Äquilanzzeichen besagt hier einfach, dass die Relation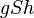 
so definiert ist.--Tutorin Anne (Diskussion) 08:38, 2. Jun. 2014 (CEST)
Aber könnten g und c nicht auch parallel sein? Dann würde h sowohl g als auch c schneiden aber g würde nicht c schneiden.
Du hast absolut Recht. Die Relation ist damit nicht transitiv, da du dies mit einem Gegenbeispiel belegt hast. --Tutorin Anne (Diskussion) 16:48, 5. Jun. 2014 (CEST)
