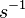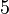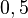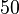Übung 10.11.14: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe I.02) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe I.08) |
||
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | <div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#B9D0F0; align:left;"> | ||
| + | {|width=90%| style="background-color:#B9D0F0; padding:1em" | ||
| + | | valign="top" | | ||
| + | <!--- hier drüber nichts eintragen ---> | ||
| + | |||
= Aufgabe I.01 = | = Aufgabe I.01 = | ||
Berechnen Sie (ggf. näherungsweise) im Kopf:<br /> | Berechnen Sie (ggf. näherungsweise) im Kopf:<br /> | ||
| Zeile 29: | Zeile 34: | ||
# <math>\sin \frac{\pi}{6}= \cos \frac{\pi}{3} = \frac{1}{2}</math> | # <math>\sin \frac{\pi}{6}= \cos \frac{\pi}{3} = \frac{1}{2}</math> | ||
# <math>\sin \frac{\pi}{3}= \cos \frac{\pi}{6} = \frac{1}{2} \sqrt{3}</math> | # <math>\sin \frac{\pi}{3}= \cos \frac{\pi}{6} = \frac{1}{2} \sqrt{3}</math> | ||
| + | = Aufgabe I.04. = | ||
| + | "Bauen" Sie die folgende App mittels einer Software Ihrer Wahl nach und erklären Sie, was die App darstellen sollen. | ||
| + | <ggb_applet width="788" height="780" version="4.2" ggbBase64="UEsDBBQACAgIAEZ0aUUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAEZ0aUUAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vttb9s4Ev7c/RWEsB+2uMQh9a7C6cJJu7gC2SbY9A7t4b7QEm2zkSWdJDt20D91f2R/0w5JSZYtW4mcN9+hdagXcsh5ZuaZIZ30f11MQzRnacbj6FQjPawhFvlxwKPxqTbLR8eu9uv7n/pjFo/ZMKVoFKdTmp9qZk/XVuPgrmdjMZgHpxp1aOD6unk8JCPr2PQd53iIHXrsYZMRhw0D0wg0hBYZfxfFn+mUZQn12bU/YVN6Efs0lzIneZ68Ozm5vb3tlbP34nR8Mh4Pe4sMBMDKo+xUKy7egbi1QbeG7K5jTE6+/n6hxB/zKMtp5DMNCa1m/P1Pb/q3PAriW3TLg3xyqrnE0tCE8fEE1PSIo6ET0SkBXRPm53zOMhhau5U659NEk91oJN6/UVcorNTRUMDnPGDpqYZ7xLJc3dV17Fqu61kwR5xyFuVFX1LMeVJK6885u1VixZWc0cQejJvzjA9DdqqNaJiBVjwapYAoLCidwW2WL0M2pGl5v1oPOYJ/0IHfMSELTKdgONUMHR+ZunPkYHxkWVitpT6xhvI4DqVUjCwP/fiBdKxjdCQaohodGttWr7B6hg3V6KoxVWOpPqYabqqupupjqj6m0aJncb9StHiwpmmpp1HXk4B+4mPDRwKwoadb05MIJX4gIlYvGwOJdRO5ftGYxa2tbh3ZEKwaUrx0xQ+Jl/1IjYy9NCK1WZU/7J604S/ljI7rPnxG/VF6VloS3WnOqVs7tHwkuNWkVg1amEv+l5/GlEYnPXdC22FG23xM7O8xoYNfYsL+Scl0/SL2UDYRfQt3zdk0E6xjeJJ4EEEWBKbtAE9YiHjQOCJAdUQsZFpwS1xki9ZBhohJExnIRaIfMZCkF8uFH6aMVxtZIEs8dFTgIsNEloGIJCUTARUhSWxAcroBPSwLWTBIzE7EtIaNTBtuDBeZsEBBaY6gDQPGwT1MriODIEOMJQ7SbWTryBG0SEzBlrYr1g5CdWRjZIuhwIvAiYoPYYSLDKENeHgSZ7wCd8LCpLKKxJFHySxfw86fBuVlHm/0DmL/5mwDa0azvLyGTpCMVilPJae1jPimH9IhC6FuuBZugNCchiKCpfxRHOWoimX1bJzSZML97JrlOYzK0Hc6pxc0Z4vfoHdWLlBOLRN1n838kAecRv8EHxEihEBU5m3JS2XedqxiFj+O0+B6mYHjoMW/WBrDAhynpzuWQXRiE92yRb5fqlc2cXvYdVzLtDyCDQ9wznwqPN4ze7ZtEEJs13MNzwXQl9tf2WpiNq8UowuWlUiOUxFMBfbi5lN2FoerR0nMo/ycJvkslSUYUGAqVBpE45BJZCWpQjHj3wzjxbWC1FCyviwTuMNqAcPxeRzGKYJw1C1QcVy0Q9XKPmJlVS8s+2DZA5c24kH1nni67CHboWplLzC6WlqhKSnVJLichmeSREB43cWkx4jSaBbx/KK8ybl/U2hKVP/Ps+kQnK0Yti6SPJHI/smGe/VvWBqxUDlRBJacxbNMeXXlmW/6s4xd0XwyiII/2BjC8YoKRsxBtOq6WnHAfD6Fgep5AR0VZv0HLFU9Ddg4ZaWGoax5FbDyLa67dOOxFPVbGk8/RfMv4DMbS+2flPr0Mz/liXBNNASKvmEr7wt4RoHgg/o4UD4DLXxBNgBkLkDUEJ3lkziVZS2ELAQB+hzPmcAUWJKYmgjXkE2hpkW59Erp2JV9LmWxLAyB4uF3IJEN+61gg9dbPVT6Mg2TCRUFdYFBSJewgDoqUt7vcbCJFZhCKgTEkCinSBhT7qTWCxcJiJNBWLO3BD9DCzUpWhbtndo7qZ2C0FQE5hoFqqcbVgOnUyBJnKdTGgUokhn1nKd+yLQVlVMsUEOUiKUpZGZ5+cJXwgoRDezBhNyvsPXvwb6m7S7w8f7Qr8giB/a/gf0NBKFVoo7Vxd95ELCo0hRInUVzWGkMYYUWuNioLnGJfvlkAegcK8OQ4tEdqZkGjJ7yBRqU/Qdlr4EOA9WVUQgdmKWsgVVcqcX8J1LrzxShiBzIR9zftOe6CaLZlKU1I+TSCADMrICH9EjhKY+JirphyAMNU04bit0pmvJIiplS8HG7p7sGcSFXgtxhFoezHPbpQFHRap+uVlgmYV0ithAbkyI+LHkx4osazwB18Dsg1XWG3OoaertrbEYyTLYlmHEtmFfz+ZBmxUiJws//ntMUCpKf2+PyUyS4HUyzEZq+Cs3FAPJSIzwH6uVZe5SuM+SgGaXlVqXNGWxXeoNohqrZN1BXTKcC4wmprk3vs/v03kFPz6F4qffxkym+SFLwauF0hTYJFNoL8Ntf/Dj7JX97BEVyBO3b0nMV66kKfB228k0l6DVZvZ4WTd22Lc/FjmdgYjlm4ToeNk0ouV3PgEpdt1wJ6GqiPWK/VggVXOzTNGcZlHD3A39VAH+J/oYSbd0Vm2Cv++jVflg/h4t2g/tpaxS5J9ngwTNFdaJS0QVQm1T453/bSVBWsRWQ0HuPNPkAV69Xj+TB6JM9fLUs9FO/BndZhoZhfPsHG4VsIbFc3zLsBv4yheJ7HEc0vIClbFjgqi0T0Xb0hWYVjHRPJn5ySmnkny1OvzeJbJZzfJqE3Of5fmUAbQP/vEv+Pz8U9HcwzL05Ud+LU67ZWDzf7tPnDUiH7ZBmhbQSs+F+xF2enzwpqk2Crnk4oGu4luvYhiG+RsC27jktPu61+zgAForit/JayIPNo4wbxhJxgnQZfUlplIlv+nYTUjOhfi0rmfwI4bcdM+rXg6r6xHnas+3sW8n7axt/BB3IOzgU+tiyeSgz+MvR9UMS5nIr5qwD5uxgSvBi20KqfNkgmwcYQH+JhBko8FkD+A9dkuWHw6SPF6jBL2J/lm1g+kFhmjcwhTDIwOackXu8WgqtzmpXo17Tv+lswUNO02UjcXXnka71R0HLHxqIjrrVH6ODqT+O7ylAwEt14rmW4xieKP3aKPvlq49tZ+WD1N9+XH62ay86bjeePDVPaLoy3/jxAfCory3+787O67njBRxle3Bf7tpcTLoF9+Qx3lF+Ndse3ORhwb36aqq5dbur2+Mgw7mjlXg3K/EDK9L2s9E9VfLr2uhrw0bfu9no+yvzbNNKqqi798Ca4APYiH8rN+L4COVdN+LfXuBrp44sVmH/gvvw1kPUmw57wpvnppsHgvlEZ6hPuidstcC3tl152MEC4bOfhHT052pb/honIbv24aGC+6YB9ccu+/CPh8QeW4+tn4lMtufDwoc/NkCddsuH0/+hytJ0daKLP2/wbIIdp+2k6bULzW1nJx/vPTvR9zo70V81D7zm2UlRFH5rIBp1C4Lo+YvCh+fSjW8IDq4qPKn/1qb8DeriT6je/wVQSwcIDOdm+NEJAADyNQAAUEsBAhQAFAAICAgARnRpRdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICABGdGlFDOdm+NEJAADyNQAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAGgKAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | = Aufgabe I.05 = | ||
| + | Eine Punktmasse <math>P</math> bewegt sich auf dem Einheitskreis <math>k</math> mit konstanter Winkelgeschwindigkeit <math>\omega</math>. Als Längeneinheit sei wie üblich die SI-Einheit Meter (<math>m</math>) vereinbart. <math>\omega</math> wird in <math>\frac{m}{s}</math> angegeben und kennzeichnet also die Bogenlänge, die <math>P</math> in einer Sekunde auf <math>k</math> zurücklegt. Mit <math>T</math> bezeichnet man die Zeit, die <math>P</math> für einen Kreisumlauf benötigt. Die Bogenlänge <math>s_b</math> ist eine Funktion der Zeit <math>t</math> und kennzeichnet die Länge des Bogens, den <math>P</math> in der Zeit <math>t</math> auf <math>k</math> zurückgelegt hat. | ||
| + | Berechnen Sie fehlenden Werte in der folgenden Tabelle. | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! <math>T</math> in <math>s^{-1}</math> !! <math>\omega</math> in <math>\frac{m}{s}</math> !! <math>t</math> in <math>s</math>!! <math>s_b</math>in <math>m</math> | ||
| + | |- | ||
| + | | <math>1</math>|| ... || <math>5</math>|| ... | ||
| + | |- | ||
| + | | ...|| <math>3</math> || <math>0,5</math>|| ... | ||
| + | |- | ||
| + | | <math>50</math> || ... || ... || <math>1000</math> | ||
| + | |} | ||
| + | |||
| + | = Aufgabe I.06 = | ||
| + | Experimentieren Sie mit der folgenden App und erläutern Sie diese. Geben Sie zusätzlich ein Formel zur Berechnung von <math>\omega</math> aus <math>T</math> an. | ||
| + | |||
| + | <ggb_applet width="849" height="830" version="4.2" ggbBase64="UEsDBBQACAgIAO57aUUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAO57aUUAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vnrjtu4Ff6dfQpCWBTJdsbmXVLqyWIvWHTRJA2aabHoBQUtcWzuyJJWoj12kB/7Ny/UF+gD5JV6SEq2xnOfSZNgk8xQlMjDc77z8eORMvl6vSjQSjetqcqjiIxwhHSZVbkpZ0fR0p4cJtHXz76YzHQ109NGoZOqWSh7FPERjXbzoDeS2E02OVhhmSK5FIdC5uSQpyfyMGGxOEyZmgpxIqnmIkJo3ZqnZfVSLXRbq0y/zuZ6oZ5XmbLe5tza+ul4fHZ2NupXH1XNbDybTUfrNo8QeF62R1F38RTMnZt0xvxwijEZ//TieTB/aMrWqjLTEXJRLc2zLx5NzkyZV2fozOR2fhQlsYzQXJvZHMJMZRyhsRtUQ6y1zqxZ6RamDro+ZruoIz9Mle75o3CFim04EcrNyuS6OYrwiNKEESxw10aoaowubTeUdEuOe2OTldFnwaq78gtynIJrK9OaaaGPohNVtBCUKU8aABT8aZbQbe2m0FPV9P2dO+QA/sIA80Y7W5C5gMJRJHhyQBN5EGN8IAQOvgwXjpCtqsJbxUik6O1bRDHF6MA1JDQUGinDIxzuYRYaGhoeGhHG8DCdh6E8jOFhDGfXxNn1d4F2N85F2sfJhnESiM/9SPjxAOzFmQziJC6It4g4733DkPObeP9dw7uuDN3YNwSHhnQPE/fL4yUfGBG7V0RksGrgw9WLXuBLv2LC09uvSB8U5zZKelmUVFwR5QPB7RclYrgpYC+4f/7nwpLsTnFeCe0dVpT8IXv/HgvG+GMsOBn3Sjfp9h5q525sR1erF61THZZ64UEECdiYMgadEIik0MRug1JEBOICuiRB0rUxYm5PcsRQgtw4wpCXF5HAL+73q0QCbLmbcdi4iHEkGCJelDgCKUJe2EDkKIMRQiABk9zqxC3LJOISOixBHBx0khY72WAwD/qwOEWMIObmkhhRiSRFsZNFwp1aysT5DkYpkhhJNxV0ETQx6CHMSBBz0QDD66o1W3Dnuqi3WfE4mrJe2nPYZYu8v7TV3ui8yk6/3cNaq9b21zAIDqPdiRcOp3MH4qNJoaa6gLLhtaMBQitVuB3s7Z9UpUU9BWi4N2tUPTdZ+1pbC7Na9LNaqefK6vUPMLrtHfRL+3N6opdZYXKjyr8BR5wJZxBtj22nS/2xneBulayqmvz1pgXioPXfdVM5/aAjzkiCSSppAqcoHKOb8EimfERwEseYxJgLDji3mXKMl8mIUcloQkB24A9s+M0Vj0RYWa+2kam1bnsoZ43bTR34rvNj+21V7G7VlSntd6q2y8aXYKCBjYvpm3JWaA+tV1UoZrLTabV+HTBlwdbxpoYeDg5MZ99VRdUg2I9UQIkx69ppaP0Y59l2FPZjsB+B+ySZfPucpNSP8O00tH4UZD241kVK+jAJ7pcxrVcRMD7kmKeMK42WpbHP+4412WkXKQnjXy4XU2BbN+28SfKBTE7Ge/yanOqm1EVgUQmZXFbLNtB6S81Hk2WrXyk7/6bM/6JnsB9fKSeJFkyHoTuPc52ZBUwM9zvolEvrX8HVcDfXs0b3ERa+5g3A+qd4yOkLt72pH5pq8WO5OgbO7Lk6GffxTNqsMbWjJpqCRp/qHfty0ypQ+Hw4D4JvIYrMqQ0AaR2IEVJLO68aX9bCnoVCGb2sVtphCjJJeOT2a6EXUNQi61lZLhe6Mdk2Q8e+XAYfl10YfNQF4tKDqunPoC17Wd2BCY+v4C1SRT1XrsgmHTvVBpwaIuWtvajybuFuXFu46hwtTNDUhVp7AiM1batiaeH9BFJT7t5Pgmed+kBB4t5+YApj1F1t4Iq4kNCJWQ8QBtDMG6DTeW7sdpAFTTyFqr/129x2G9pf/NHkuS63/qoS6OSTAupWB2LXWoctsZ1YQ/heSAZE6BJzY4rsxRQl7LPJEb5rjsQgR6TPEaj3R8wROHBDmgZytMvSum5gNWemA/n9Ozig12CQoq/Q+1/RGB2HU/r6hMK0vYySkYhxnMLxJeOUJ6mUd8zd9X7WnZuPs6p9/P4dOGufHEAhUPadJz0GK2BS1VwWRP9ka/J6/g20+f9AQK+9reMQvMRLlsQM8zSVgsWMe0LhUSq5EDEnCRdxnMJb5Buf9/uTaKD3bTjDMtVY3cJJdXMGXvUZwAcIP0G/R3W/mK80LgO8e7A1cJ/9LhOPt2umodkijm+JOH4Q4qRfx0fjyqRzFWm4u3eGDpHMqsVClTkq/QsOKMqyjXaFtcIeWUWcSIbgl7Z/8OfGgk6VRncbpDN1AefCG+1xHMz6oAS/I9xquTaFUc3mQqVzd+rewMx/r3tu2ss14bYMBUOfC0f9CflJWelQvYGX9F68pL9JXu4hCrYu3+YO131A1Q04OmM9OuqTojcU0VD48JGQklCZQlXEuKSx5+chH3HMaUokZTQWaZzcBmN6+bmlfynPnVpmURcmM/Y20rC5tHCwd5eGzWcjDVccX0ExPrw2XMPkzQUmT+/A5OlnwuRDNkqk4JyKhAhOqf8m0xE8wEnSNAGOMxBgIWP5Eah8G33e3KjP7F76zH6T+nxRHI712pJOHn73y7Kyf/jyn9VCz9TRl6ELRe7j5+pY//SP9+/+5UrecDv8vkwzLFiMzpv/lFCa1nu///3If0Rt4X3uZPvBHTTiRfeftuHjKo56hvbfUiy8Krxy0oHcnqEjlgoQdy4JXIDIdxIk05gQ2Cw8wYwSPtSjm5NBzyXje6PRrNAmm5/89z/Nwsw0+lOjTTvVZ3q2LGddGm6RhU9bcFxEDktCKCAkKGYs9sjFIzgiQWdYwmhKBU6vQm48/IrmP2l3/6X97H9QSwcIeJKgED8IAACCHwAAUEsBAhQAFAAICAgA7ntpRdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICADue2lFeJKgED8IAACCHwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAANYIAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | = Aufgabe I.07 = | ||
| + | Bauen Sie die folgende App nach und erläutern Sie die Entseheung von Lissajousfiguren. | ||
| + | |||
| + | <ggb_applet width="849" height="830" version="4.2" ggbBase64="UEsDBBQACAgIAGiFaUUAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIAGiFaUUAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s5Vpbb9vIFX7O/ooBsSiS1pbmxiGZyllkF1hsACc1ardY9IJgRI6kiSlSSw5lKchDX/vr9i/1zAwp0ZLvbu20TSKPhpw5c853vnMhndF3q3mOlqqqdVkcBWSAA6SKtMx0MT0KGjM5jIPv3nwzmqpyqsaVRJOymktzFPABDbb7YDYQ2G7WGUhhqSSZCA9DkZFDnkzEYcyi8DBhchyGE0EVDwOEVrV+XZQf5FzVC5mq03Sm5vK4TKVxMmfGLF4PhxcXF4Pu9EFZTYfT6XiwqrMAgeZFfRS0X16DuEubLphbTjEmw5/fH3vxh7qojSxSFSBrVaPffPNidKGLrLxAFzozs6MgjkSAZkpPZ2BmIqIADe2iBdi6UKnRS1XD1t7U2Wzmi8Atk4W9/8J/Q/nGnABleqkzVR0FeEBpzAgOcTsGqKy0Kky7lLRHDjtho6VWF16q/eYO5DgB1Za61uNcHQUTmddglC4mFQAK+lQNTGuzztVYVt18qw45gL+wQH9WVhZ4zqNwFIQ8PqCxOIgwPghD7HXpHxwgU5a5k4pRmKAvXxDFFKMDOxA/UBiE8Lewv4aZH6gfuB9Cv4b77dwv5X4N92s4u8HOdr41tL1wydLOTta3k4B99iPg4wDYsTPu2UmsEV8Qsdq7gSGrN3H624G3U+GnkRsI9gNpb8b2h8NLPNIi9iCLSO9Uz4frD93jS3dizJO7n0gfZefGSnqVlTS8xspHgtsdSsJ+UEAs2H/us3cku5ed10J7jxMFf0zsP+DACD/FgaNhl+lGbeyhembXtnQ1al7brMMSl3gQQSEEpoggT4SIJDBENkApIiHiIUxJjIQdI8RsTHLEUIzsOsKQSy9hDD+4i1eBQpBlL0Y+cBHjKGSIuKTEEaQi5BIbJDnKYEUYohA22dOJPZYJxAVMWIw4KGhTWmTTBoN9MIfDKWIEMbuXRIgKJCiKbFok3GZLEVvdQShFAiNht0JehJzo8yHsiBGz1gDDF2WtN+DOVL7YeMXhqItFYy5hl86z7qspd1ZnZXr+/Q7WStam+w6LoBhtK54vTpcK4otRLscqh7bh1NIAoaXMbQQ7+ZOyMKijAPXXppVczHRanypjYFeNPsmlPJZGrX6E1XWnoDva1emRatJcZ1oWfwaOWBFWINqUbZuXurId4/aUtCyr7HRdA3HQ6i+qKm3+oAPOSIxJImgMVRTK6NrfEgkfEBxHESYR5iEHnOtUWsaLeMCoYDQmkHbgDwT8+ppboT9ZLTeWyZWqOyinlY2mFnw7eVd/X+bbS4tSF+YHuTBN5VowyIGVteltMc2Vg9ZlVWhm0vNxuTr1mDIv62y9gBn2CoynP5R5WSGIRxpCizFtx7Ef3Rqr2WYVdmuwW4E7J+lsc58k1K1w49iPbhV43avWWko6MwnujtG1yyIgvM8xRxnbGjWFNsfdxOj0vLWU+PUfmvkY2NZuuyyS/JtEjoY7/Bqdq6pQuWdRAZ5syqb2tN5Q88WoqdWJNLO3RfZHNYV4PJE2JRoQ7ZduNc5Uquew0V9voZPWrX8CVf3VTE0r1VmYu57XA+vu4j6n9y47UT9W5fxdsTwDzuyoOhp29ozqtNILS000hhx9rrbsy3QtIcNn/X1gfA1WpDbbAJDGghgg2ZhZWbm2FmIWGmX0oVwqiymkScIDG6+5mkNTi4xjZdHMVaXTjYfOPq5dwwxaNq0hyaA1xToIleNPkF12/LqFE25fw1wk88VM2jabtPyUa1Crj5WT9r7M2oPbdXVu+3M01z6rzuXKURjJcV3mjYEnFHBOsX1C8Zq1+QdaEvv8s7LRFdtva9udhfbbRK96GANs+jMQ6jI7tjFkICueQ99fu0A3bUi7Lz/pLFPFRl9ZAKGcWyC/LTy1F0r5oNhsXID5LpX0qNC6xjpptajgLCukhfjXf4JnEFyH89Fv0a//QENkneWqwM0+dVt3nIoHIokJg4SKI8i1kHjv6b9L2t54vNk9Wwwo/2oYhVtGibsyKtwySpCWUQQq1BMyChTAt7Cqlz/v6Kazj6tdR4X/I5Hv34GsbQ5g/5WRv9qP/NUdI3/PqWRAQyFYhAXhLExIRB8T+XvanmyUfWkOoLksXlolQG/z6lUHguumrtK/vdET9RD2idipb4exHzYG4DsSsF/Ta8shl7MshfAggT+UYM4pZjER4NrP/hWdfyFlTbD936VW21/daQ76QKblfC6LDBXuyQ0o3dTB9olB4hZYSWw+9RY3prv1h8pAqBRaUS+2FbYHb+7EduD1dt2Mcq+vugtJ7omxbFY617Ja7zVx9w/B26jZVdCXaVlbXq4dLw/gc29qrr8aah7iAeNxGFHMI0ZJTNwT0rrj7BORc30rOdmDyMn+T8h5plaGtvT8zS9NaX5/rOtafoKnm4meNpUq/NVgn5rwcL5lppfznJjVRlbmxHIKueo7YFBqCOUxDiFjsshxMxokkX3WZzGjCTyhJ32i3o4UuYTUt38r52oqP66OvvUX0O/Qy2N5pn7+qy0+f38Fc3+jxfCK+N4DkTwriLp2+u8+rbpXNjXU+Mnm9R5E8/v2V0T+VQ5u3/ld5xA+oAwgZwmPEhyHrM0VgjMhcBzFjHNBwuv8sZMLIAquq1Ortytd76WD9JYsYAV2EKfP6oJthu3aRwfyZ5dx95qABzeN6pfCb2mdpueLXKfaPAD4NgevrwQ+uwfw2VcC/GH3gIW3yO/XuieG/l1h3yMBKDv4px79bA/5k5uR3+ksvv6+4vla4Ft7DPKgHuN5U/3T9hjsysq5vrJyrh9WOZ+3ZfvPVs6QhTHFJGKCxdSXznAAdZRRnlAaJdDniOtK57D/ztb9AqX9DxRv/gVQSwcIvX6EI1QIAADwIQAAUEsBAhQAFAAICAgAaIVpRdY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICABohWlFvX6EI1QIAADwIQAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAOsIAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
| + | |||
| + | = Aufgabe I.08 = | ||
| + | <iframe src="http://www.ph-heidelberg.de/wp/gieding/Lehre/cg/beispiele/videos/Lissajous_5zu3.swf" width="400" height="300" frameborder="2"></iframe> | ||
| + | |||
| + | Hier schwingt ein Pendel an einem zweiten. Sie dürfen die beiden Pendel als mathematische Pendel modellieren (Wikipedia hilft). Geben Sie eine allgemeine Parameterdarstellung der gezeichneten Kurve an. | ||
| + | |||
| + | <!--- hier drunter nichts eintragen ---> | ||
| + | [[Kategorie:Linalg]] | ||
| + | |||
| + | |} | ||
| + | </div> | ||
Aktuelle Version vom 9. November 2014, 17:16 Uhr
Aufgabe I.01Berechnen Sie (ggf. näherungsweise) im Kopf:
Aufgabe I.02Generieren Sie ein Tabellenkalkulationsblatt, in dem die Tabelle aus Aufgabe I.01 automatisch berechnet wird. Bedingung: Sie dürfen die Funktion "Bogenmaß()" nicht verwenden. Aufgabe I.03Beweisen Sie: Aufgabe I.04."Bauen" Sie die folgende App mittels einer Software Ihrer Wahl nach und erklären Sie, was die App darstellen sollen. Aufgabe I.05Eine Punktmasse
Aufgabe I.06Experimentieren Sie mit der folgenden App und erläutern Sie diese. Geben Sie zusätzlich ein Formel zur Berechnung von
Aufgabe I.07Bauen Sie die folgende App nach und erläutern Sie die Entseheung von Lissajousfiguren.
Aufgabe I.08[ www.ph-heidelberg.de is not an authorized iframe site ] Hier schwingt ein Pendel an einem zweiten. Sie dürfen die beiden Pendel als mathematische Pendel modellieren (Wikipedia hilft). Geben Sie eine allgemeine Parameterdarstellung der gezeichneten Kurve an. |
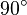

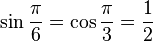
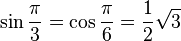
 bewegt sich auf dem Einheitskreis
bewegt sich auf dem Einheitskreis  mit konstanter Winkelgeschwindigkeit
mit konstanter Winkelgeschwindigkeit 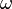 . Als Längeneinheit sei wie üblich die SI-Einheit Meter (
. Als Längeneinheit sei wie üblich die SI-Einheit Meter ( ) vereinbart.
) vereinbart. 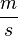 angegeben und kennzeichnet also die Bogenlänge, die
angegeben und kennzeichnet also die Bogenlänge, die 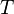 bezeichnet man die Zeit, die
bezeichnet man die Zeit, die 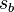 ist eine Funktion der Zeit
ist eine Funktion der Zeit  und kennzeichnet die Länge des Bogens, den
und kennzeichnet die Länge des Bogens, den