Lösung von Aufgabe 10.5: Unterschied zwischen den Versionen
(→Beweis Versuch 1:) |
(→Beweis Versuch 1:) |
||
| (5 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
Es sei <math> SW^{+} </math> eine Winkelhalbierende des Winkels <math> \angle ASB </math>.<br /> | Es sei <math> SW^{+} </math> eine Winkelhalbierende des Winkels <math> \angle ASB </math>.<br /> | ||
Dann gilt: <math>| \angle ASW| = | \angle WSB |= 1/2 | \angle ASB| </math> | Dann gilt: <math>| \angle ASW| = | \angle WSB |= 1/2 | \angle ASB| </math> | ||
| + | |||
| + | ==Lösung--[[Benutzer:Schnirch|Schnirch]] 13:21, 21. Jul. 2010 (UTC) -Beweis von Löwenzahn wurde weitgehend übernommen== | ||
| + | Voraussetzung: <math> SW^{+} </math> eine Winkelhalbierende des Winkels <math> \angle ASB </math><br /> | ||
| + | Behauptung: <math>| \angle ASW| = | \angle WSB |= 1/2 | \angle ASB| </math> | ||
| + | |||
| + | {| class="wikitable " | ||
| + | |+ Beweis | ||
| + | ! Nr. | ||
| + | ! Beweisschritt | ||
| + | ! Begründung | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(I) | ||
| + | | <math> SW^{+} </math> eine Winkelhalbierende von <math> \angle ASB </math> | ||
| + | | (VSS) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(II) | ||
| + | | <math>| \angle ASW| + | \angle WSB |= | \angle ASB| </math> | ||
| + | | Winkeladditionsaxiom, W liegt im Innern von <math>\angle ASB</math> | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(III) | ||
| + | | <math>| \angle ASW| = | \angle WSB | </math> | ||
| + | | (I), Def. Winkelhalbierende | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(IV) | ||
| + | | <math>| \angle ASW| + | \angle ASW |= | \angle ASB| </math> | ||
| + | | (II), (III), (Rechnen mit reellen Zahlen) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(V) | ||
| + | | <math>2| \angle ASW| = | \angle ASB| </math> --> <math> | \angle ASW |= 1/2| \angle ASB| </math> | ||
| + | | (IV), (Rechnen mit reellen Zahlen) | ||
| + | |- | ||
| + | ! style="background: #FFDDDD;"|(VI) | ||
| + | | <math>| \angle ASW| =| \angle WSB| = 1/2| \angle ASB| </math> | ||
| + | | (III), (V) | ||
| + | |} | ||
| + | |||
| + | ==vorangegangene Diskussion== | ||
== Beweis Versuch 1: == | == Beweis Versuch 1: == | ||
| Zeile 44: | Zeile 81: | ||
Bei dem Satz wird nicht zwischen Existenz und Eindeutigkeit der Winkelhalbierenden unterschieden. Das kommt doch nur vor, wenn "genau" im Satz steht. Kann es sein dass du den Satz: "Jeder Winkel hat genau eine Winkelhalbierende" meinst? Da muss man dann nämlich Existenz und Eindeutigkeit beweisen. Hier ist nur gezeigt, dass bei einer Winkelhalbierenden (VSS) die Winkel, die durch die Winkelhalbierenden entstehen gleichgroß sind und diese das halbe Maß des Gesamtwinkel (Beh) haben. --[[Benutzer:Löwenzahn|Löwenzahn]] 17:56, 6. Jul. 2010 (UTC) | Bei dem Satz wird nicht zwischen Existenz und Eindeutigkeit der Winkelhalbierenden unterschieden. Das kommt doch nur vor, wenn "genau" im Satz steht. Kann es sein dass du den Satz: "Jeder Winkel hat genau eine Winkelhalbierende" meinst? Da muss man dann nämlich Existenz und Eindeutigkeit beweisen. Hier ist nur gezeigt, dass bei einer Winkelhalbierenden (VSS) die Winkel, die durch die Winkelhalbierenden entstehen gleichgroß sind und diese das halbe Maß des Gesamtwinkel (Beh) haben. --[[Benutzer:Löwenzahn|Löwenzahn]] 17:56, 6. Jul. 2010 (UTC) | ||
| + | |||
| + | HI, oh, ja da hast du Recht - hab da im falschen Satz geschaut - alles klar - dann stimmt ja alles =) --[[Benutzer:TimoRR|TimoRR]] 21:55, 6. Jul. 2010 (UTC) | ||
| + | |||
| + | <br /><br /> | ||
| + | [[Bild:Dozenten.jpg]]<br /> | ||
| + | Wo ist denn jetzt der Existenz-und Eindeutigkeitsbeweis der Winkelhalbierenden? Also das ist er auf jedenfall nicht. Hier wird ja die Existenz schon in der Voraussetzung vorrausgesetzt, und die Eindeutigkeit wird auch nicht bewisen. Bekommen wir da noch eine Antwort? --[[Benutzer:TheGeosi|TheGeosi]] 10:41, 28. Jul. 2010 (UTC) | ||
| + | |||
| + | Ich glaube der Beweis der Ex und Eind der Winkelhalbierenden wurde im Tutorium 11 Aufg.1 bewiesen. --[[Benutzer:Löwenzahn|Löwenzahn]] 11:58, 28. Jul. 2010 (UTC)<br /> | ||
| + | |||
| + | Ok, hab ich auch gesehen. Haben wir aber irgendwie ausgelassen. Wird im Beweis über die Wineklkonsturktion eines halbsogroßen Winkels wie Winkel ASB und dann die Winkeladdition gegangen oder? --[[Benutzer:TheGeosi|TheGeosi]] 12:36, 28. Jul. 2010 (UTC) | ||
Aktuelle Version vom 28. Juli 2010, 13:36 Uhr
Satz VI.1/2:
Es sei 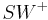 eine Winkelhalbierende des Winkels
eine Winkelhalbierende des Winkels  .
.
Dann gilt: 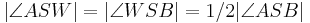
Lösung--Schnirch 13:21, 21. Jul. 2010 (UTC) -Beweis von Löwenzahn wurde weitgehend übernommen
Voraussetzung: 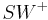 eine Winkelhalbierende des Winkels
eine Winkelhalbierende des Winkels 
Behauptung: 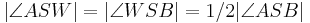
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 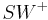 eine Winkelhalbierende von eine Winkelhalbierende von 
|
(VSS) |
| (II) | 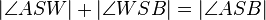
|
Winkeladditionsaxiom, W liegt im Innern von 
|
| (III) | 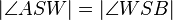
|
(I), Def. Winkelhalbierende |
| (IV) | 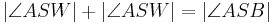
|
(II), (III), (Rechnen mit reellen Zahlen) |
| (V) | 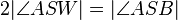 --> --> 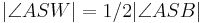
|
(IV), (Rechnen mit reellen Zahlen) |
| (VI) | 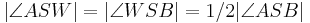
|
(III), (V) |
vorangegangene Diskussion
Beweis Versuch 1:
VSS: 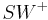 eine Winkelhalbierende des Winkels
eine Winkelhalbierende des Winkels 
Beh: 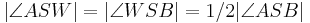
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 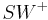 eine Winkelhalbierende von eine Winkelhalbierende von 
|
(VSS) |
| (II) | 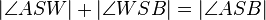
|
Winkeladditionsaxiom, W liegt im Innern von 
|
| (III) | 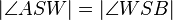
|
(I), Def. Winkelhalbierende |
| (IV) | 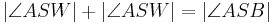
|
(II), (III), (rechnen mit reellen Zahlen) |
| (V) | 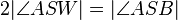 --> --> 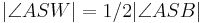
|
(IV), (rechnen mit reellen Zahlen) |
| (VI) | 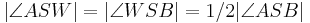
|
(III), (V) |
qed --Löwenzahn 17:51, 1. Jul. 2010 (UTC)
Das war ja jetzt der Beweis für die Existenz, fehlt jetzt noch einer für die Eindeutigkeit!? Wenn ja, wie sähe der dann aus!? Reicht dafür das Winkelkonstruktionsaxiom!? --TimoRR 17:00, 6. Jul. 2010 (UTC)
Bei dem Satz wird nicht zwischen Existenz und Eindeutigkeit der Winkelhalbierenden unterschieden. Das kommt doch nur vor, wenn "genau" im Satz steht. Kann es sein dass du den Satz: "Jeder Winkel hat genau eine Winkelhalbierende" meinst? Da muss man dann nämlich Existenz und Eindeutigkeit beweisen. Hier ist nur gezeigt, dass bei einer Winkelhalbierenden (VSS) die Winkel, die durch die Winkelhalbierenden entstehen gleichgroß sind und diese das halbe Maß des Gesamtwinkel (Beh) haben. --Löwenzahn 17:56, 6. Jul. 2010 (UTC)
HI, oh, ja da hast du Recht - hab da im falschen Satz geschaut - alles klar - dann stimmt ja alles =) --TimoRR 21:55, 6. Jul. 2010 (UTC)

Wo ist denn jetzt der Existenz-und Eindeutigkeitsbeweis der Winkelhalbierenden? Also das ist er auf jedenfall nicht. Hier wird ja die Existenz schon in der Voraussetzung vorrausgesetzt, und die Eindeutigkeit wird auch nicht bewisen. Bekommen wir da noch eine Antwort? --TheGeosi 10:41, 28. Jul. 2010 (UTC)
Ich glaube der Beweis der Ex und Eind der Winkelhalbierenden wurde im Tutorium 11 Aufg.1 bewiesen. --Löwenzahn 11:58, 28. Jul. 2010 (UTC)
Ok, hab ich auch gesehen. Haben wir aber irgendwie ausgelassen. Wird im Beweis über die Wineklkonsturktion eines halbsogroßen Winkels wie Winkel ASB und dann die Winkeladdition gegangen oder? --TheGeosi 12:36, 28. Jul. 2010 (UTC)

