Was ist eine Gruppe? SoSe 2017: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Das Linkseinslement ist auch Rechtseinslement) |
(→Halbgruppe) |
||
| (30 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
=Beispiele für Gruppen= | =Beispiele für Gruppen= | ||
==endliche Gruppen== | ==endliche Gruppen== | ||
| + | |||
===Die Gruppe der Deckabbildungen des Rechtecks=== | ===Die Gruppe der Deckabbildungen des Rechtecks=== | ||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! !! id!! <math>D_{180}</math>!! <math>S_h</math>!! <math>S_v</math> | ||
| + | |- | ||
| + | | <math>id</math> || <math>id</math> || <math>D_{180}</math>|| <math>S_h</math> || <math>S_v</math> | ||
| + | |- | ||
| + | | <math>D_{180}</math>|| <math>D_{180}</math> || <math>id</math> || <math>S_v</math> || <math>S_h</math> | ||
| + | |- | ||
| + | | <math>S_h</math> || <math>S_h</math> || <math>S_v</math> || <math>id</math> || <math>D_{180}</math> | ||
| + | |- | ||
| + | | <math>S_v</math> || <math>S_v</math> || <math>S_h</math> || <math>D_{180}</math>|| <math>id</math> | ||
| + | |} | ||
===Die Gruppe der Deckabbildungen der Raute=== | ===Die Gruppe der Deckabbildungen der Raute=== | ||
| + | |||
==unendliche Gruppen== | ==unendliche Gruppen== | ||
=== Gebrochene Zahlen: <math>[\mathbb{Q}^+, \cdot ]</math> === | === Gebrochene Zahlen: <math>[\mathbb{Q}^+, \cdot ]</math> === | ||
| Zeile 14: | Zeile 28: | ||
=Gruppendefinitionen= | =Gruppendefinitionen= | ||
==Die "übliche" Gruppendefinition (lange Version)== | ==Die "übliche" Gruppendefinition (lange Version)== | ||
| − | + | '''Definition 1a: (Gruppe Langfassung)''' | |
| + | ----- | ||
| + | Es sei <math>G</math> eine nichtleere Menge auf der eine Verknüpfung <math>\odot</math>. <br /> | ||
Wenn die folgenden Axiome erfüllt sind, heißt die Struktur <math>\mathbb{G}:=[G, \odot ]</math> Gruppe:<br /> | Wenn die folgenden Axiome erfüllt sind, heißt die Struktur <math>\mathbb{G}:=[G, \odot ]</math> Gruppe:<br /> | ||
# <math>\odot</math> ist auf <math>G</math> abgeschlossen: <math>\forall a,b \in G: a \odot b \in G</math> | # <math>\odot</math> ist auf <math>G</math> abgeschlossen: <math>\forall a,b \in G: a \odot b \in G</math> | ||
| Zeile 20: | Zeile 36: | ||
# Bezüglich <math>\odot</math> existiert in <math>G</math> ein ("universelles") Einslement <math>e</math>: <math>\exist e \in G \forall a \in G: a \odot e = e \odot a= a </math>. | # Bezüglich <math>\odot</math> existiert in <math>G</math> ein ("universelles") Einslement <math>e</math>: <math>\exist e \in G \forall a \in G: a \odot e = e \odot a= a </math>. | ||
# Bezüglich <math>\odot</math> existiert zu jedem <math>a</math> aus <math>G</math> ein ("persönliches") inverses Element <math>a^{-1}</math>: <math>\forall a \in G \exist a^{-1} \in G: a \odot a^{-1} = a^{-1} \odot a = e</math>. | # Bezüglich <math>\odot</math> existiert zu jedem <math>a</math> aus <math>G</math> ein ("persönliches") inverses Element <math>a^{-1}</math>: <math>\forall a \in G \exist a^{-1} \in G: a \odot a^{-1} = a^{-1} \odot a = e</math>. | ||
| − | + | ||
==Die "übliche" Gruppendefinition (kurze Version)== | ==Die "übliche" Gruppendefinition (kurze Version)== | ||
| − | + | '''Definition 1b: (Gruppe, Kurzfassung)''' | |
| + | ----- | ||
| + | Es sei <math>G</math> eine nichtleere Menge auf der eine Verknüpfung <math>\odot</math>. <br /> | ||
Wenn die folgenden Axiome erfüllt sind, heißt die Struktur <math>\mathbb{G}:=[G, \odot ]</math> Gruppe:<br /> | Wenn die folgenden Axiome erfüllt sind, heißt die Struktur <math>\mathbb{G}:=[G, \odot ]</math> Gruppe:<br /> | ||
# <math>\odot</math> ist auf <math>G</math> abgeschlossen: <math>\forall a,b \in G: a \odot b \in G</math> | # <math>\odot</math> ist auf <math>G</math> abgeschlossen: <math>\forall a,b \in G: a \odot b \in G</math> | ||
# <math>\odot</math> ist assoziativ auf <math>G</math>: <math>\forall a, b, c \in G: (a \odot b) \odot c = a \odot (b \odot c)</math> | # <math>\odot</math> ist assoziativ auf <math>G</math>: <math>\forall a, b, c \in G: (a \odot b) \odot c = a \odot (b \odot c)</math> | ||
# Bezüglich <math>\odot</math> existiert in <math>G</math> ein ("universelles") Einslement <math>e</math>: <math>\exist e \in G \forall a \in G: e \odot a= a </math>. | # Bezüglich <math>\odot</math> existiert in <math>G</math> ein ("universelles") Einslement <math>e</math>: <math>\exist e \in G \forall a \in G: e \odot a= a </math>. | ||
| − | # Bezüglich <math>\odot</math> existiert zu jedem <math>a</math> aus <math>G</math> ein ("persönliches") inverses Element <math>a^{-1}</math>: <math>\forall a \in G \exist a^{-1} \in G: a^{-1} \odot a = e</math>. | + | # Bezüglich <math>\odot</math> existiert zu jedem <math>a</math> aus <math>G</math> ein ("persönliches") inverses Element <math>a^{-1}</math>: <math>\forall a \in G \exist a^{-1} \in G: a^{-1} \odot a = e</math>. |
| − | == Das Linkseinslement ist auch | + | |
| + | ==Ordnung einer Gruppe== | ||
| + | '''Definition 2: (Gruppenordnung)''' | ||
| + | ----- | ||
| + | : Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente.<br /> | ||
| + | Kurzschreibweise: Wenn <math>n</math> die Ordnung der Gruppe <math>G</math> ist: <math>|G|=n</math> | ||
| + | |||
| + | ==Ordnung einer Gruppenelements== | ||
| + | '''Definition 3: (Ordung eines Gruppenelements)''' | ||
| + | ----- | ||
| + | Es sei <math>[G,\odot]</math> eine Gruppe mit dem Einselement <math>e</math> und <math>g\in G</math>. Die kleinste natürliche Zahl <math>n</math> mit <math>n>0</math>, für die gilt <math>g^n=e</math> heißt Ordnung von <math>g</math>.<br /> | ||
| + | Kurzschreibweise: <math>|g|=n</math> | ||
| + | |||
| + | ==Halbgruppe== | ||
| + | '''Definition 4: (Halbgruppe)''' | ||
| + | ----- | ||
| + | :Eine Menge <math>H</math> auf der eine Verknüpfung <math>\odot</math> definiert ist, heißt Halbgruppe, wenn <math>\odot</math> abgeschlossen auf <math>H</math> und assoziativ ist. | ||
| + | <br /> | ||
| + | Bemerkung: Tutor Alex wies darauf hin, dass die Menge <math>H</math> auch die leere Menge sein darf. Er hat recht. Ich habe das geändert.--[[Benutzer:*m.g.*|*m.g.*]] ([[Benutzer Diskussion:*m.g.*|Diskussion]]) 16:43, 14. Mai 2017 (CEST) | ||
| + | (Bitte dazu in die Diskussion schauen! (Update)) | ||
| + | |||
| + | ==Monoid== | ||
| + | '''Definition 5: (Monoid)''' | ||
| + | ----- | ||
| + | :Eine Halbgruppe mit Einselement heißt Monoid. | ||
| + | |||
| + | == Das Linkseinslement ist auch Rechtseinselement== | ||
Die lange Version der Gruppendefinition fordert, dass wenn das Einselement <math>e</math> sowohl rechtsseitig als auch linksseitig multipliziert mit einem beliebigen Gruppenelement <math>a</math> multipliziert eben dieses Element <math>a</math> das Ergebnis dieser Multiplikation ist. Die kurze Version der Gruppendefinition fordert nur die Existenz eines linksseitigen Einslementes. In der Tat ist die Korrektheit der Gruppendefinition gewährleistet, wenn die Existenz des Einselementes nur linksseitig (oder rechtsseitig) gefordert wird. | Die lange Version der Gruppendefinition fordert, dass wenn das Einselement <math>e</math> sowohl rechtsseitig als auch linksseitig multipliziert mit einem beliebigen Gruppenelement <math>a</math> multipliziert eben dieses Element <math>a</math> das Ergebnis dieser Multiplikation ist. Die kurze Version der Gruppendefinition fordert nur die Existenz eines linksseitigen Einslementes. In der Tat ist die Korrektheit der Gruppendefinition gewährleistet, wenn die Existenz des Einselementes nur linksseitig (oder rechtsseitig) gefordert wird. | ||
Gleiches gilt für die Forderung nach der Existenz linksseitiger bzw. rechtsseitiger inverser Elemente. <br /> | Gleiches gilt für die Forderung nach der Existenz linksseitiger bzw. rechtsseitiger inverser Elemente. <br /> | ||
| − | Es gilt der Satz: | + | Es gilt der Satz:<br /> |
| − | + | ||
| + | ====Satz 1==== | ||
| + | :Wenn in einer Halbgruppe ein linksseitiges Einselement und zu jedem Element der Halbgruppe ein linksseitiges inverses Element existiert, so sind dieses Linkseinselement und diese Linksinversen gleichzeitig Rechtseinselement und Rechtsinverse.<br /> | ||
| + | ====Beweis von Satz 1==== | ||
| + | Übungsaufgabe, Hinweise | ||
| + | # Beginnen Sie mit Linksinvers=Rechtsinvers | ||
| + | # Multiplizieren Sie zunächst das Linksinverse <math>g^{-1}</math> eines beliebigen Elementes <math>g</math> von rechts mit <math>g</math>:<math>g \odot g^{-1}</math> | ||
| + | # Ersetzen Sie <math>g</math> durch <math>e \odot g</math> | ||
| + | # Ersetzen Sie <math>e</math> durch das Produkt des Linksinversen vom Linksinversen von <math>g</math> mit dem Linksinversen von <math>g</math>: <math>(g^{-1})^{-1} \odot g^{-1}</math>. | ||
| + | # Der Rest ist geschicktes Klammern und Ausnutzung der Assoziativität... | ||
| + | |||
| + | '''Beweis:''' | ||
| + | ------ | ||
| + | Es sei <math>g^{-1}</math> das Linksinverse von <math>g</math>.<br /> | ||
| + | |||
| + | Wir muliplizieren <math>g^{-1}</math> von rechts mit <math>g</math>:<br /> | ||
| + | (I) <math>g \cdot g^{-1}</math><br /> | ||
| + | (II) <math>g \cdot g^{-1}= e \cdot g \cdot g^{-1}</math><br /> | ||
| + | Wissen: Auch <math>g^{-1}</math> hat ein Linksinverses: <math>(g^{-1})^{-1}</math><br /> | ||
| + | Ersetzen <math>e</math> durch <math>(g^{-1})^{-1}\cdot g^{-1}</math><br /> | ||
| + | |||
| + | (III) <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1} \cdot g \cdot g^{-1}</math><br /> | ||
| + | (IV) geschicktes Klammern: <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot (g^{-1} \cdot g) \cdot g^{-1}</math><br /> | ||
| + | (V) Klammer berechnen:<math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot e \cdot g^{-1}</math><br /> | ||
| + | (VI) Mit <math>e</math> multiplizieren ist geschenkt ... <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}</math><br /> | ||
| + | (VII) <math>(g^{-1})^{-1}\cdot g^{-1}</math> bedeutet, das Linksinverse vom Linksinversen von <math>g</math> mieinander multiplizieren. <br /> | ||
| + | (VII) also <math>(g^{-1})^{-1}\cdot g^{-1}=e</math> <br /> | ||
| + | (IX) und damit <math>g \cdot g^{-1}= (g^{-1})^{-1}\cdot g^{-1}=e</math> <br /> | ||
| + | (X) oder einfach: <math>g \cdot g^{-1}=e</math> und damit: Das Linksinverse <math>g^{-1}</math> von <math>g</math> ist auch sein Rechtsinverses <br /> | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 16. Mai 2017, 12:41 Uhr
Beispiele für Gruppenendliche GruppenDie Gruppe der Deckabbildungen des Rechtecks
Die Gruppe der Deckabbildungen der Rauteunendliche Gruppen Gebrochene Zahlen:
|
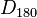
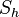
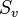
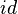
![[\mathbb{Q}^+, \cdot ]](/images/math/2/9/8/298e82ce4345a135cfc73e8ba6154d2b.png)
![[\mathbb{Z}, +]](/images/math/8/2/8/828d3197747f0dc881f51c684f1a4c7d.png)
 eine nichtleere Menge auf der eine Verknüpfung
eine nichtleere Menge auf der eine Verknüpfung  .
. ![\mathbb{G}:=[G, \odot ]](/images/math/b/6/2/b62276da8758fad83c54ead688c9ecca.png) Gruppe:
Gruppe: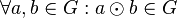
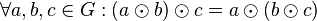
 :
: 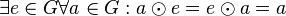 .
.
 aus
aus 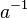 :
: 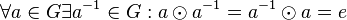 .
.
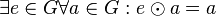 .
.
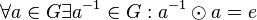 .
.
 die Ordnung der Gruppe
die Ordnung der Gruppe 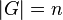
![[G,\odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe mit dem Einselement
eine Gruppe mit dem Einselement 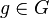 . Die kleinste natürliche Zahl
. Die kleinste natürliche Zahl 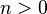 , für die gilt
, für die gilt 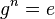 heißt Ordnung von
heißt Ordnung von  .
.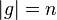
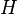 auf der eine Verknüpfung
auf der eine Verknüpfung 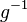 eines beliebigen Elementes
eines beliebigen Elementes 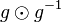

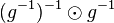 .
.
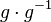
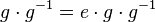
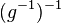
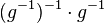
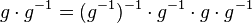
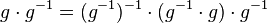
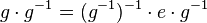
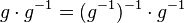
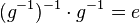
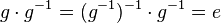
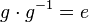 und damit: Das Linksinverse
und damit: Das Linksinverse 
