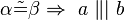Lösung von Aufgabe 4.08 S SoSe 17: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
(→Lösung 1) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
{|width=90%| style="background-color:#FFFF99; padding:1em" | {|width=90%| style="background-color:#FFFF99; padding:1em" | ||
| valign="top" | | | valign="top" | | ||
| + | ==Aufgabe 4.08== | ||
| + | Gegeben seien in der Ebene <math>\varepsilon</math> zwei nicht identische Geraden <math>a</math> und <math>b</math>. Sowohl <math>a</math> als auch <math>b</math> mögen durch eine dritte Gerade <math>c</math> jeweils in genau einem Punkt geschnitten werden. Beweisen Sie: Wenn bei diesem Schnitt kongruente Stufenwinkel entstehen, dann sind <math>a</math> und <math>b</math> parallel zueinander.<br /> | ||
| + | Hinweis: Führen Sie den Beweis indirekt, indem Sie annehmen, dass <math>a </math> und <math>b</math> nicht parallel sind. Jetzt dürfen Sie den schwachen Außenwinkelsatz (Jeder Außenwinkel ist größer als jeder nichtanliegende Innenwinkel.) anwenden.<br /> | ||
| + | ==Lösung 1== | ||
| + | <math>\alpha \tilde {=} \beta \Rightarrow \ a \ \|| \ b </math><br/> | ||
| + | Annahme: | ||
| + | a und b sind nicht parallel, wenn α und β gleich groß sind. | ||
| + | ==Lösung 2== | ||
</div> | </div> | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
Aktuelle Version vom 18. Mai 2017, 16:31 Uhr
Aufgabe 4.08Gegeben seien in der Ebene Lösung 1
Annahme: a und b sind nicht parallel, wenn α und β gleich groß sind. Lösung 2 |
zwei nicht identische Geraden 
und 
. Sowohl 
jeweils in genau einem Punkt geschnitten werden. Beweisen Sie: Wenn bei diesem Schnitt kongruente Stufenwinkel entstehen, dann sind 
