Lösung von Aufgabe 1.3 SoSe 2017: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 1.3. Algebra SoSe 2017)
 
(2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 +
<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;">
 +
{|width=90%| style="background-color:#CCFFCC; padding:1em"
 +
| valign="top" |
 +
 +
 
=Aufgabe 1.3. Algebra SoSe 2017=
 
=Aufgabe 1.3. Algebra SoSe 2017=
 
Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.
 
Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.
Zeile 16: Zeile 21:
 
:Unter der Klein'schen Vierergruppe versteht man eine Gruppe der Ordnung 4, in der alle Gruppenelemente zu sich selbst invers sind.
 
:Unter der Klein'schen Vierergruppe versteht man eine Gruppe der Ordnung 4, in der alle Gruppenelemente zu sich selbst invers sind.
  
−
'''Definition: Zyklische Gruppe'''
+
{| class="wikitable"
 +
|-
 +
| <math>\odot</math> || e|| a|| b|| c
 +
|-
 +
| e|| Beispiel || Beispiel || Beispiel || Beispiel
 +
|-
 +
| a|| Beispiel || Beispiel || Beispiel || Beispiel
 +
|-
 +
| b|| Beispiel || Beispiel || Beispiel || Beispiel
 +
|-
 +
| c|| Beispiel || Beispiel || Beispiel || Beispiel
 +
|}
 +
 
 +
'''Definition: "andere Vierergruppe'''
 
-----
 
-----
−
:Unter einer Zyklischen Gruppe versteht man eine Gruppe der Ordnung 4, die von einem der Gruppenelemente erzeugt wird.
+
:zyklische Viergruppe
 +
 
 +
<!--- Was hier drunter steht muss stehen bleiben --->
 +
|}
 +
</div>
 +
[[Kategorie:Algebra]]

Aktuelle Version vom 15. Mai 2017, 10:12 Uhr


Aufgabe 1.3. Algebra SoSe 2017

Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.

  1. Geben Sie für jede der beiden Gruppen zwei Beispiele an.
  2. Definieren Sie was man unter der Klein'schen Vierergruppe versteht.
  3. Definieren Sie die andere der beiden Vierergruppen.

Lösungen: zu 1.

  • Deckdrehungen des Qudrates: zyklische Gruppe
  • \mathbb{Z} mod 4: zyklische Gruppe
  • Deckabbildungen des Rechtecks: Klein'sche Vierergruppe
  • Deckabbildungen der Raute: Klein'sche Vierergruppe

Definition: Klein'sche Vierergruppe

Unter der Klein'schen Vierergruppe versteht man eine Gruppe der Ordnung 4, in der alle Gruppenelemente zu sich selbst invers sind.
\odot e a b c
e Beispiel Beispiel Beispiel Beispiel
a Beispiel Beispiel Beispiel Beispiel
b Beispiel Beispiel Beispiel Beispiel
c Beispiel Beispiel Beispiel Beispiel

Definition: "andere Vierergruppe

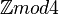zyklische Viergruppe
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_1.3_SoSe_2017&oldid=29733“