|
Aufgabe 1.3. Algebra SoSe 2017
Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.
- Geben Sie für jede der beiden Gruppen zwei Beispiele an.
- Definieren Sie was man unter der Klein'schen Vierergruppe versteht.
- Definieren Sie die andere der beiden Vierergruppen.
Lösungen:
zu 1.
- Deckdrehungen des Qudrates: zyklische Gruppe
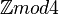 : zyklische Gruppe : zyklische Gruppe
- Deckabbildungen des Rechtecks: Klein'sche Vierergruppe
- Deckabbildungen der Raute: Klein'sche Vierergruppe
Definition: Klein'sche Vierergruppe
- Unter der Klein'schen Vierergruppe versteht man eine Gruppe der Ordnung 4, in der alle Gruppenelemente zu sich selbst invers sind.
 |
e |
a |
b |
c
|
| e |
Beispiel |
Beispiel |
Beispiel |
Beispiel
|
| a |
Beispiel |
Beispiel |
Beispiel |
Beispiel
|
| b |
Beispiel |
Beispiel |
Beispiel |
Beispiel
|
| c |
Beispiel |
Beispiel |
Beispiel |
Beispiel
|
Definition: "andere Vierergruppe
- zyklische Viergruppe
| 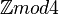 : zyklische Gruppe
: zyklische Gruppe


