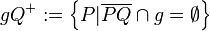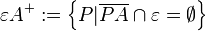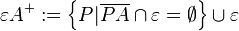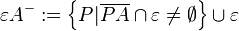Lösung von Aufgabe 7.03 SoSe 2017: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;"> {|width=90%| style="backgro…“) |
(→Lösung 1) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
| valign="top" | | | valign="top" | | ||
| + | Es sei <math>\varepsilon</math> eine Ebene und <math>A</math> ein Punkt außerhalb von <math>\varepsilon</math>.<br\> | ||
| + | Definieren Sie Halbraum <math>\varepsilon A^+</math> und Halbraum <math>\varepsilon A^-</math>. | ||
=Lösung 1= | =Lösung 1= | ||
| + | Definition offener Halbebene: <br /> | ||
| + | <math>gQ^+ := \left\{ P|\overline {PQ} \cap g =\empty \right\}</math> | ||
| + | |||
| + | Zweckdienliche Umformung für den Raum:<br /> | ||
| + | <math> \varepsilon A^+ := \left\{ P|\overline{PA} \cap \varepsilon=\empty \right\}</math> | ||
| + | |||
| + | Zum Schluss und damit auch dem Abschluss der Halbräume noch <math> \varepsilon</math> hinzufügen: | ||
| + | |||
| + | <math> \varepsilon A^+ := \left\{ P|\overline{PA} \cap \varepsilon=\empty \right\} \cup \varepsilon</math><br /> | ||
| + | |||
| + | <math> \varepsilon A^- := \left\{ P|\overline{PA} \cap \varepsilon \not = \empty \right\} \cup \varepsilon</math> | ||
| + | |||
=Lösung 2= | =Lösung 2= | ||
Aktuelle Version vom 22. Juni 2017, 15:53 Uhr
|
Es sei Lösung 1Definition offener Halbebene: Zweckdienliche Umformung für den Raum: Zum Schluss und damit auch dem Abschluss der Halbräume noch
Lösung 2 |
 eine Ebene und
eine Ebene und  ein Punkt außerhalb von
ein Punkt außerhalb von 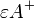 und Halbraum
und Halbraum 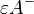 .
.