Gruppendefinition (Gleichung): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#CCFFCC; align:left;"> {|width=90%| style="backgro…“) |
(→Beweis von Satz 7: kleine Ergänzung bzgl. x=y=a^{-1}) |
||
| (10 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 11: | Zeile 11: | ||
In jeder Gruppe <math>[G, \odot]</math> gilt: Jedes Gruppenelement <math>g \in G</math> hat genau ein inverses Element. | In jeder Gruppe <math>[G, \odot]</math> gilt: Jedes Gruppenelement <math>g \in G</math> hat genau ein inverses Element. | ||
==Beweis von Satz 4== | ==Beweis von Satz 4== | ||
| − | Es sei <math>g \in G</math>. Nach der Definition des Begriffs Gruppe hat <math>g</math> in <math>G</math> ein Inverses <math>g_1^{-1}</math>. | + | Es sei <math>g \in G</math> eine Gruppe mit dem Einslement <math>e</math>. Nach der Definition des Begriffs Gruppe hat <math>g</math> in <math>G</math> ein Inverses <math>g_1^{-1}</math> bezüglich <math>\odot</math>. Wir nehmen an, <math>g</math> hat in <math>G</math> ein weiteres Inverses <math>g_2^{-1}</math>, das natürlich von <math>g_1^{-1}</math> verschieden ist. Nach Satz 1 wissen wir, dass <math>g_1^{-1}</math> und <math>g_2^{-1}</math> von links und von rechts invers zu <math>g</math> bzgl. <math>\odot</math> sind. <br /> |
| + | |||
| + | Die triviale Gleichung <math>(I) e=e</math> "pumpen" wir zu <math>(II) g \odot g_1^{-1} = g \odot g_2^{-1}</math> auf. <br /> | ||
| + | |||
| + | <math>(II)</math> multiplizieren wir auf beiden Seiten von links mit <math>g_1^{-1}</math> und erhalten <math>(III) g_1^{-1} \odot g \odot g_1^{-1}= g_1^{-1} \odot g \odot g_2^{-1}</math>.<br /> | ||
| + | |||
| + | <math>(III)</math> verkürzt sich zu <math>g_1^{-1}=g_2^{-1}</math>, was ein Widerspruch zu unserer Annahme <math>g_1^{-1} \neq g_2^{-1}</math> ist. | ||
| + | |||
| + | =Kürzbarkeit= | ||
| + | ==Satz 5== | ||
| + | Es sei <math>[G, \odot]</math> eine Gruppe. Für alle Elemente <math>a, b, c \in G</math> gilt: <br /> | ||
| + | # <math>a\odot b = a \odot c \Rightarrow b=c</math> | ||
| + | # <math>b \odot a= c \odot a \Rightarrow b=c</math> | ||
| + | ==Beweis von Satz 5== | ||
| + | Jeweils von rechts bzw. links beide Seiten der Gleichung mit <math>a^{-1}</math> multiplizieren. | ||
| + | =Lösbarkeit der Gleichungen= | ||
| + | ==Satz 6== | ||
| + | In jeder Gruppe <math>[G, \odot]</math> sind die Gleichungen | ||
| + | # <math>a \odot x= b</math> und | ||
| + | # <math>y \odot a = b</math> | ||
| + | jeweils eindeutig lösbar. | ||
| + | ==Beweis von Satz 6== | ||
| + | Wir führen den Beweis nur für die Gleichung <math>a \odot x= b</math>, für die Gleichung <math>y \odot a = b</math> wird der Beweis analog geführt.<br /> | ||
| + | ===Existenzbeweis=== | ||
| + | Zuerst formen wir <math>a\odot x=b</math> um: | ||
| + | |||
| + | <math>a\odot x=b</math> <math>|\odot a^{-1}</math> | ||
| + | |||
| + | <math>a^{-1}\odot a \odot x = a^{-1} \odot b</math> | ||
| + | |||
| + | <math>e\odot x = a^{-1} \odot b</math> | ||
| + | |||
| + | <math>x = a^{-1} \odot b</math> | ||
| + | |||
| + | |||
| + | |||
| + | <math>x=a^{-1}\odot b</math> setzen wir nun in <math>a\odot x=b</math> ein und formen um: <math>a \odot (a^{-1}\odot b) = (a \odot a^{-1}) \odot b = e \odot b = b</math>. | ||
| + | |||
| + | ===Eindeutigkeitsbeweis=== | ||
| + | Es seien <math>x_1</math> und <math>x_2</math> Lösungen der Gleichung <math>a \odot x= b</math>. Damit folgt <math>a \odot x_1 = a \odot x_2</math>. Nach Satz 5 gilt <math>x_1=x_2</math> | ||
| + | =Ein Monoid in dem die Gleichungen lösbar sind, ist eine Gruppe= | ||
| + | ==Satz 7== | ||
| + | Es sei <math>[M, \odot]</math> ein Monoid. <math>e</math> sei das Einslement dieses Monoids. Wenn die Gleichungen | ||
| + | # <math>a \odot x = b</math> und | ||
| + | # <math>y \odot a = b</math> | ||
| + | in <math>[M, \odot ]</math>lösbar sind, dann ist das Monoid sogar eine Gruppe. | ||
| + | ==Beweis von Satz 7== | ||
| + | Wir haben zu zeigen, dass zu jedem Element <math>a \in M</math> ein Inverses in <math>M</math> existiert. Wegen der Lösbarkeit der Gleichungen 1 und 2 sind auch die Gleichungen <br /> | ||
| + | * <math>a \odot x = e</math> und | ||
| + | * <math>y \odot a = e</math> | ||
| + | lösbar. | ||
| + | |||
| + | Daraus folgt, dass <math>x,y</math> Inverse von <math>a</math> sind, also <math>x=y=a^{-1}</math> (nach Satz 4). | ||
| + | |||
| + | =Weitere Möglichkeit der Gruppendefinition= | ||
| + | Die Sätze 6 und 7 erlauben, eine Gruppe als ein Monoid zu definieren, in dem die Gleichungen | ||
| + | # <math>a \odot x = b</math> und | ||
| + | # <math>y \odot a = b</math> | ||
| + | lösbar sind. | ||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
|} | |} | ||
</div> | </div> | ||
[[Kategorie:Algebra]] | [[Kategorie:Algebra]] | ||
Aktuelle Version vom 13. Juli 2018, 14:56 Uhr
Eindeutigkeit des EinslementesSatz 3Jede Gruppe hat genau ein Einslement. Beweis von Satz 3Es sei Eindeutigkeit der inversen ElementeSatz 4In jeder Gruppe Beweis von Satz 4Es sei Die triviale Gleichung
KürzbarkeitSatz 5Es sei Beweis von Satz 5Jeweils von rechts bzw. links beide Seiten der Gleichung mit Lösbarkeit der GleichungenSatz 6In jeder Gruppe
jeweils eindeutig lösbar. Beweis von Satz 6Wir führen den Beweis nur für die Gleichung ExistenzbeweisZuerst formen wir
EindeutigkeitsbeweisEs seien Ein Monoid in dem die Gleichungen lösbar sind, ist eine GruppeSatz 7Es sei
in Beweis von Satz 7Wir haben zu zeigen, dass zu jedem Element
lösbar. Daraus folgt, dass Weitere Möglichkeit der GruppendefinitionDie Sätze 6 und 7 erlauben, eine Gruppe als ein Monoid zu definieren, in dem die Gleichungen
lösbar sind. |
![[G, \odot]](/images/math/7/3/5/73557169bfbd888213d4a53d2c3ff1e4.png) eine Gruppe. Nach der Definition des Begriffs Gruppe hat
eine Gruppe. Nach der Definition des Begriffs Gruppe hat 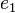 . Es bleibt zu zeigen, dass
. Es bleibt zu zeigen, dass 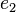 hat. Wir nehmen an es gibt
hat. Wir nehmen an es gibt 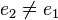 . Nach Satz 2 sind
. Nach Satz 2 sind 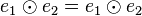 . Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente
. Aus dieser Gleichung folgt wegen der Einslement eigenschaft beider Elemente 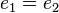 .
.
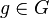 hat genau ein inverses Element.
hat genau ein inverses Element.
 . Nach der Definition des Begriffs Gruppe hat
. Nach der Definition des Begriffs Gruppe hat  in
in  ein Inverses
ein Inverses 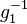 bezüglich
bezüglich  . Wir nehmen an,
. Wir nehmen an, 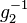 , das natürlich von
, das natürlich von 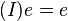 "pumpen" wir zu
"pumpen" wir zu 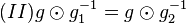 auf.
auf. 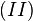 multiplizieren wir auf beiden Seiten von links mit
multiplizieren wir auf beiden Seiten von links mit 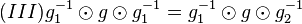 .
.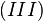 verkürzt sich zu
verkürzt sich zu 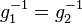 , was ein Widerspruch zu unserer Annahme
, was ein Widerspruch zu unserer Annahme 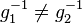 ist.
ist.
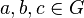 gilt:
gilt: 

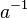 multiplizieren.
multiplizieren.
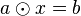 und
und
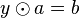
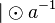
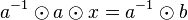
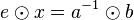
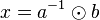
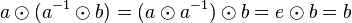 .
.
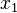 und
und 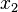 Lösungen der Gleichung
Lösungen der Gleichung 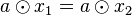 . Nach Satz 5 gilt
. Nach Satz 5 gilt 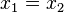
![[M, \odot]](/images/math/1/b/7/1b76d279ea0a66347bff1d26e034943a.png) ein Monoid.
ein Monoid. 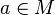 ein Inverses in
ein Inverses in  existiert. Wegen der Lösbarkeit der Gleichungen 1 und 2 sind auch die Gleichungen
existiert. Wegen der Lösbarkeit der Gleichungen 1 und 2 sind auch die Gleichungen 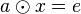 und
und
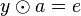
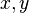 Inverse von
Inverse von  sind, also
sind, also 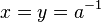 (nach Satz 4).
(nach Satz 4).

