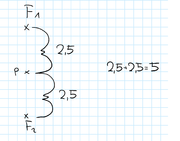Serie 1 SoSe 2018: Unterschied zwischen den Versionen
(→Aufgabe 1.3 SoSe 2018) |
(→Aufgabe 1.10 SoSe 2018) |
||
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
=Aufgabe 1.3 SoSe 2018= | =Aufgabe 1.3 SoSe 2018= | ||
Verwenden Sie den Oberbegriff Viereck (dieser sei definiert) um den Begriff Trapez zu definieren. | Verwenden Sie den Oberbegriff Viereck (dieser sei definiert) um den Begriff Trapez zu definieren. | ||
| − | <br /> | + | <br /><br /> |
| + | |||
Ein Viereck mit einem Paar paralleler Seiten heißt Trapez. | Ein Viereck mit einem Paar paralleler Seiten heißt Trapez. | ||
=Aufgabe 1.4 SoSe 2018= | =Aufgabe 1.4 SoSe 2018= | ||
| − | Definieren Sie den Begriff Parallelogramm mittels des nächsthöheren Oberbegriffs. | + | Definieren Sie den Begriff Parallelogramm mittels des nächsthöheren Oberbegriffs.<br /> |
| + | |||
| + | <br /> | ||
| + | Ein Trapez mit zwei Paaren paralleler Seiten heißt Parallelogramm. | ||
=Aufgabe 1.5 SoSe 2018= | =Aufgabe 1.5 SoSe 2018= | ||
| Zeile 29: | Zeile 33: | ||
'''Definition: (Rechteck)'''<br /> | '''Definition: (Rechteck)'''<br /> | ||
Wenn in einem Parallelogramm die Diagonalen ..... , dann heißt das Parallelogramm Rechteck. | Wenn in einem Parallelogramm die Diagonalen ..... , dann heißt das Parallelogramm Rechteck. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | Wenn in einem Parallelogramm die Diagonalen gleich lang sind, denn heißt das Parallelogramm Rechteck. | ||
=Aufgabe 1.6 SoSe 2018= | =Aufgabe 1.6 SoSe 2018= | ||
Warum ist die folgende Definition nicht korrekt?<br /> | Warum ist die folgende Definition nicht korrekt?<br /> | ||
'''Definition: (Raute)'''<br /> | '''Definition: (Raute)'''<br /> | ||
| − | Es gibt Drachen, deren Seiten alle gleichlang sind. Sie heißen Rauten. | + | Es gibt Drachen, deren Seiten alle gleichlang sind. Sie heißen Rauten.<br /> |
| + | <br /> | ||
| + | Definitionen mit "es gibt" zählen nicht als Definition. | ||
=Aufgabe 1.7 SoSe 2018= | =Aufgabe 1.7 SoSe 2018= | ||
| − | Es sei <math>\overline{ABCD}</math> ein Viereck. Definieren Sie, was man unter den Diagonalen von <math>\overline{ABCD}</math> versteht. | + | Es sei <math>\overline{ABCD}</math> ein Viereck. Definieren Sie, was man unter den Diagonalen von <math>\overline{ABCD}</math> versteht.<br /> |
| + | <br /> | ||
| + | Unter den Diagonalen versteht man die Strecken <math>\overline{AC}</math> und <math>\overline{BD}</math>. | ||
=Aufgabe 1.8 SoSe 2018= | =Aufgabe 1.8 SoSe 2018= | ||
Wir setzen ebene Geometrie voraus. Es seien <math>F_1</math> und <math>F_2</math> zwei verschiedene Punkte. Zeichnen Sie eine Beispiel für die Punktenge <math>\varepsilon := \{P| |PF_1|+|PF_2|=5\}</math>. | Wir setzen ebene Geometrie voraus. Es seien <math>F_1</math> und <math>F_2</math> zwei verschiedene Punkte. Zeichnen Sie eine Beispiel für die Punktenge <math>\varepsilon := \{P| |PF_1|+|PF_2|=5\}</math>. | ||
| + | <br /> | ||
| + | <br /> | ||
| + | [[Datei:Aufgabe 1.8.png|thumb|Lösung zu Aufgabe 1.8 aus Serie 1]] | ||
=Aufgabe 1.9 SoSe 2018= | =Aufgabe 1.9 SoSe 2018= | ||
| − | Es seien <math>k_1</math> und <math>k_2</math> zwei Kreise mit den Mittelpunkten <math>M_1</math> und <math>M_2</math> und den Radien <math>r_1</math> und <math>r_2</math>. Für <math>|M_1M_2|=\pi</math> und <math>r_1=r_2=1,13</math> definieren wir die folgende Menge Kreisolix<math>:= k_1 \cap k_2</math>. Wie wird Kreisolix üblicherweise genannt? | + | Es seien <math>k_1</math> und <math>k_2</math> zwei Kreise mit den Mittelpunkten <math>M_1</math> und <math>M_2</math> und den Radien <math>r_1</math> und <math>r_2</math>. Für <math>|M_1M_2|=\pi</math> und <math>r_1=r_2=1,13</math> definieren wir die folgende Menge Kreisolix<math>:= k_1 \cap k_2</math>. Wie wird Kreisolix üblicherweise genannt?<br /> |
| + | <br /> | ||
| + | Leere Menge. Die Radien <math>r_1</math> und <math>r_1</math> sind in der Summe kleiner als der Abstand von <math>M_1</math> zu <math>M_1</math>. Somit ergeben sich aus der definierten Schnittmenge <math>k_1 \cap k_2</math> keine gemeinsamen Punkte. | ||
=Aufgabe 1.10 SoSe 2018= | =Aufgabe 1.10 SoSe 2018= | ||
| − | Es sei <math>s</math> die von <math>AB</math> verschieden Symmetrieachse der Strecke <math>\overline{AB}</math>. Wie wird <math>s</math> auch genannt? | + | Es sei <math>s</math> die von <math>AB</math> verschieden Symmetrieachse der Strecke <math>\overline{AB}</math>. Wie wird <math>s</math> auch genannt?<br /> |
| + | <br /> | ||
| + | Mittelsenkrechte<br /> | ||
| + | <br /> | ||
| + | |||
<!--- Was hier drunter steht muss stehen bleiben ---> | <!--- Was hier drunter steht muss stehen bleiben ---> | ||
Aktuelle Version vom 26. April 2018, 16:21 Uhr
Inhaltsverzeichnis |
Aufgabe 1.1 SoSe 2018
Ergänzen Sie die folgende Definition für die ebene Geometrie:
Definition: (Kreis)
Es seien  ein beliebiger aber fester Punkt und
ein beliebiger aber fester Punkt und  eine positive reelle Zahl.
eine positive reelle Zahl.
Unter dem Kreis  versteht man die Menge aller Punkte
versteht man die Menge aller Punkte  , deren
, deren
Abstand zum Punkt  gleich
gleich  ist.
ist.
Aufgabe 1.2 SoSe 2018
Ergänzen Sie die folgende Definition:
Definition: (arithmetisches Mittel von 5 Zahlen)
Es seien 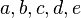 fünf reelle Zahlen. Das arithmetische Mittel
fünf reelle Zahlen. Das arithmetische Mittel  dieser fünf Zahlen berechnet sich wie folgt: ...
dieser fünf Zahlen berechnet sich wie folgt: ...
Man nehme die Summe der Zahlen  ,
,  ,
,  ,
,  und
und  und teile sie durch ihre Anzahl.
und teile sie durch ihre Anzahl.
Aufgabe 1.3 SoSe 2018
Verwenden Sie den Oberbegriff Viereck (dieser sei definiert) um den Begriff Trapez zu definieren.
Ein Viereck mit einem Paar paralleler Seiten heißt Trapez.
Aufgabe 1.4 SoSe 2018
Definieren Sie den Begriff Parallelogramm mittels des nächsthöheren Oberbegriffs.
Ein Trapez mit zwei Paaren paralleler Seiten heißt Parallelogramm.
Aufgabe 1.5 SoSe 2018
Ergänzen Sie die folgende Definition:
Definition: (Rechteck)
Wenn in einem Parallelogramm die Diagonalen ..... , dann heißt das Parallelogramm Rechteck.
Wenn in einem Parallelogramm die Diagonalen gleich lang sind, denn heißt das Parallelogramm Rechteck.
Aufgabe 1.6 SoSe 2018
Warum ist die folgende Definition nicht korrekt?
Definition: (Raute)
Es gibt Drachen, deren Seiten alle gleichlang sind. Sie heißen Rauten.
Definitionen mit "es gibt" zählen nicht als Definition.
Aufgabe 1.7 SoSe 2018
Es sei  ein Viereck. Definieren Sie, was man unter den Diagonalen von
ein Viereck. Definieren Sie, was man unter den Diagonalen von  versteht.
versteht.
Unter den Diagonalen versteht man die Strecken  und
und 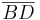 .
.
Aufgabe 1.8 SoSe 2018
Wir setzen ebene Geometrie voraus. Es seien 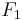 und
und 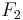 zwei verschiedene Punkte. Zeichnen Sie eine Beispiel für die Punktenge
zwei verschiedene Punkte. Zeichnen Sie eine Beispiel für die Punktenge 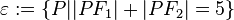 .
.
Aufgabe 1.9 SoSe 2018
Es seien 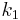 und
und 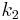 zwei Kreise mit den Mittelpunkten
zwei Kreise mit den Mittelpunkten 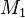 und
und  und den Radien
und den Radien 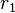 und
und 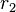 . Für
. Für 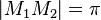 und
und 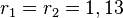 definieren wir die folgende Menge Kreisolix
definieren wir die folgende Menge Kreisolix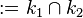 . Wie wird Kreisolix üblicherweise genannt?
. Wie wird Kreisolix üblicherweise genannt?
Leere Menge. Die Radien 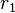 und
und 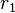 sind in der Summe kleiner als der Abstand von
sind in der Summe kleiner als der Abstand von 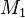 zu
zu 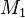 . Somit ergeben sich aus der definierten Schnittmenge
. Somit ergeben sich aus der definierten Schnittmenge 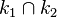 keine gemeinsamen Punkte.
keine gemeinsamen Punkte.
Aufgabe 1.10 SoSe 2018
Es sei  die von
die von  verschieden Symmetrieachse der Strecke
verschieden Symmetrieachse der Strecke  . Wie wird
. Wie wird  auch genannt?
auch genannt?
Mittelsenkrechte