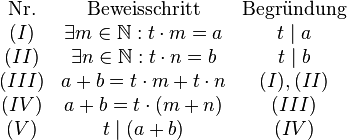Lösung von Aufgabe 2.1 SoSe 2018: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „=Aufgabe 2.1 SoSe 2018= Ein Blick über den Tellerrand der Geometrie:<br /> '''Satz S:'''<br /> :<math>\forall t, a, b \in \mathbb{Z}: t \mid a \land t \mid b…“)
 
(→‎Lösung)
 
(Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt)
Zeile 1: Zeile 1:
 +
<div style="margin:0; margin-right:4px; border:1px solid #27408B; padding: 1em 1em 1em 1em; background-color:#FFFF99; align:left;">
 +
{|width=90%| style="background-color:#FFFF99; padding:1em"
 +
| valign="top" |
 +
<!--- Was hier drüber steht muss stehen bleiben --->
 +
 
=Aufgabe 2.1 SoSe 2018=
 
=Aufgabe 2.1 SoSe 2018=
 
Ein Blick über den Tellerrand der Geometrie:<br />
 
Ein Blick über den Tellerrand der Geometrie:<br />
Zeile 10: Zeile 15:
  
 
=Lösung=
 
=Lösung=
−
a) Wenn zwei Zahlen durch jeweils durch eine dritte Zahl teilbar sind, so ist auch ihre Summe durch diese dritte Zahl teilbar.<br />
+
a) Wenn zwei Zahlen jeweils durch eine dritte Zahl teilbar sind, so ist auch ihre Summe durch diese dritte Zahl teilbar.<br />
 
b) <math>t</math> teilt sowohl <math>a</math> als auch <math>b</math>.<br />
 
b) <math>t</math> teilt sowohl <math>a</math> als auch <math>b</math>.<br />
 
c) <math>t</math> teilt die Summe der beiden Zahlen <math>a</math> und <math>b</math><br />
 
c) <math>t</math> teilt die Summe der beiden Zahlen <math>a</math> und <math>b</math><br />
Zeile 23: Zeile 28:
 
(V) & t \mid (a+b) & (IV)
 
(V) & t \mid (a+b) & (IV)
 
\end{matrix}
 
\end{matrix}
 +
</math>
  
−
 
+
<!--- Was hier drunter steht muss stehen bleiben --->
−
</math>
+
|}
 +
</div>
 +
[[Kategorie:Einführung_S]]

Aktuelle Version vom 21. Mai 2018, 17:06 Uhr

Aufgabe 2.1 SoSe 2018

Ein Blick über den Tellerrand der Geometrie:

Satz S:

\forall t, a, b \in \mathbb{Z}: t \mid a \land t \mid b \Rightarrow t \mid (a+b)

a) Formulieren Sie Satz S schultauglich, d.h. weniger formal in einem normalen deutschen Satz.
b) Wie lautet die Voraussetzung in Satz S?
c) Wie lautet die Behauptung von Satz S.
d) Beweisen Sie Satz S.

Lösung

a) Wenn zwei Zahlen jeweils durch eine dritte Zahl teilbar sind, so ist auch ihre Summe durch diese dritte Zahl teilbar.
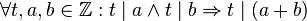
b) t teilt sowohl a als auch b.
c) t teilt die Summe der beiden Zahlen a und b
d) Der Beweis:
\begin{matrix} \text{Nr.} & \text{Beweisschritt} & \text{Begründung} \\ (I) & \exist m \in \mathbb{N}: t \cdot m = a & t \mid a \\ (II) & \exist n \in \mathbb{N}: t \cdot n = b & t \mid b \\ (III) & a + b = t \cdot m + t \cdot n & (I), (II) \\ (IV) & a + b = t \cdot (m + n) & (III) \\ (V) & t \mid (a+b) & (IV) \end{matrix}

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_2.1_SoSe_2018&oldid=31607“