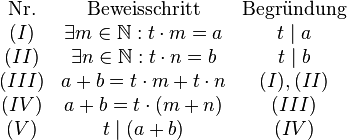Lösung von Aufgabe 2.1 SoSe 2018

Aufgabe 2.1 SoSe 2018 Ein Blick über den Tellerrand der Geometrie: Satz S: $\forall t, a, b \in \mathbb{Z}: t \mid a \land t \mid b \Rightarrow t \mid (a+b)$ a) Formulieren Sie Satz S schultauglich, d.h. weniger formal in einem normalen deutschen Satz. b) Wie lautet die Voraussetzung in Satz S? c) Wie lautet die Behauptung von Satz S. d) Beweisen Sie Satz S. Lösung a) Wenn zwei Zahlen jeweils durch eine dritte Zahl teilbar sind, so ist auch ihre Summe durch diese dritte Zahl teilbar. 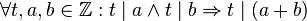b) $t$ teilt sowohl $a$ als auch $b$. c) $t$ teilt die Summe der beiden Zahlen $a$ und $b$ d) Der Beweis: $\begin{matrix} \text{Nr.} & \text{Beweisschritt} & \text{Begründung} \\ (I) & \exist m \in \mathbb{N}: t \cdot m = a & t \mid a \\ (II) & \exist n \in \mathbb{N}: t \cdot n = b & t \mid b \\ (III) & a + b = t \cdot m + t \cdot n & (I), (II) \\ (IV) & a + b = t \cdot (m + n) & (III) \\ (V) & t \mid (a+b) & (IV) \end{matrix}$