Lösung von Aufgabe 10.1P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
CIG UA (Diskussion | Beiträge) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
<ggb_applet width="649" height="515" version="4.2" ggbBase64="UEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vzdctu2Er5OnwLDi3MVSQT/ROVI6URqfpw4beY4p9M5NxmIhChEFMmSlH8yfZy+SV/sLACSIiVKlmRZodxqbIMgFljg28XuR9B2/8fbuY+uaZywMBgouK0qiAZO6LLAGyiLdNKylR9f/tD3aOjRcUzQJIznJB0oRltTlv2g1rZU3pm5A0WdTDSHqnbLwdhtGbo+aY1N3W1NyMRwbU3Hlu0oCN0m7EUQ/kzmNImIQ6+cKZ2Ty9AhqRhzmqbRi07n5uamnWtvh7HX8bxx+zZxFQQzD5KBkl28gOEqnW50Ia6pKu789vFSDt9iQZKSwKEK4qtasJc/POvfsMANb9ANc9PpQLHMroKmlHlTWKalwpo6XCiCtUbUSdk1TaBrqSrWnM4jRYiRgLc/k1fIL5ajIJddM5fGgE9bVw0DG6oqSwWFMaNBmkniTGMnH6t/zeiNHJRfCX3QKQ1Df0z4eOiPP5Cmaip6zgssCw0Ky5JNqryn6rLQZGHIwpQyhuxuSFFDyhhSxtDB2CxhY58OlAnxE8CPBZMYbFfUk/TOp2I+2Y3l2vFzWFPCvoGwzgGVgMN9VX3OvwHl50aOdGmRuKQ1jRdblcr2ks5co2X0dteoPWideq5Tq1ulZtbrtB+Gba4TmyWdoEp8ie91XK0tKiWQR9aobwN2VeNGU+6h0DJOvURD7XWPvsguBr/pahuVdtVT4Nrv5BGonwUdlEy5bLYpUzpPeBjSe8js8WiCkQkhx+pC8DAR7kHR1RAEGYRNZJhQxTayeNlFehcaDKQjG3E5rCMRc0wbfhhdMZiFTBiM3+1CqEMYFBnI1BEWocpAEKCQCHcQ+jQdJEwTmdCJq8caH0K3kGFBTbeRAXPkka6LQVCHjlAH9RrSMdJ5Z9xFmoUsPh42eAS1bD51GFJDlooszAeEYAmBUgZJkLeRzlcD2yoKE1agO6V+lIMkcGRBtEgr2DlzN79Mw6iwoZB2Q2c2LLDOWihJ0rIYpIllKpJpo5KpnvV9MqY+5PMr7ggIXROfRyqhYRIGKcqdQJP3vJhEU+YkVzRNoVeCvpJrcklSevsGpJNct1AtEmifLhyfuYwEv4KX8CH4gKjIpzz+5vnU0LtSixOGsXt1l4DroNv/0TiEoKkBgyh/IJzeySbdxtUmQDpxCHd6c6UTBJq7DU2WVE2vi6WRW1osCHkxK2zBry+SYei7RXMUsiAdkShdxIIcwexivqhXgedTga1IH0AznNk4vL2SoOpyrM93EdRUOYGxNwr9MEawJTXTBIGsHMtSyPCZFVKqkFGFhJpbiblFO+5pQkKUY1kKKTC7nFq2UpyvEqu5GpZIzqZU3Uw4DWcti4Cll3klZc4sWyqWHX5ezMfgbxlu1THxscbsd1ZcrD+jcUB96UgB2HIRLhLp2YV3PusvEvqJpNNXgfsf6sGe/ER4XExhaCm6nLJLHTaHjvJ+Bh7hhv0vTFXedakX03yJvuCjElrRqpbdeu22GOpNHM4vguvP4DUrU+138vX0EydmEXdONIZAPaNL/3NZQiDMu+V+sPgEVuHwiANAphxEBZFFOg1jQTlh2wLBQO//+jMIaAyBEtgm37E+nQPhRKlwS+HZhXleCR7L7YDC8VeII0XikO1L1KC51kWFMxM/mhLOdTMIfHIHEyiDIsb7GLqrUIElxHogNkTSJyJKpTvJ+cJFBMOJXVgyt8A+QbcDpaXxR5E7/lwC5Tf5XCNZPF8q35qVMCjvrlgNnE6idA9ew/PHC58QrtH5w6VmcGlHgssJ53MSuCgQrO1T6N95YaAs+QJR+a5EBHNnQ0TjIEqEFmneDnHRh8SDpZgjxQgU+kAZS4WZmhr7SIW5BYqhqhkkBVIwgwfSRKS5NEto4uIdc10qKE9nu3FLcJati01d2NfEWYpbmhfvY97NPphQj9eKiTj3eOH+E93TD9e9Sc+8qYW1YrADwAef8LnvXgQ80VGRGtZT44zSiHOSX4LPMQkSfqpTzYm7Q0maA2Ue9ls4w/K8kBw3B8kig7byIGc0GspqjvlpHcgqBT2DJKOfMCe/Pi1ev0wmCU0F8bBkItVOhSY+AZpvnoD3mStJ6RQU5yfJXV5L7vJmE8XRpNhEirmS4tCDKI52HIpTtW5jOM7kPj88YT7J95+ak5xeo9PJKpRug6AsUvN5ZOZVKGmToMSrLAfjRoNZTTRvn0CiyZ3ZPEFifveE8FLb9iMk5ktw+pWs/Fam23dr6djbnnL5/imA9Q7c9NWD7yPsePFrC+U8ZLeNw/c7/T2QXRJ5fs3mkc8clu7jlBdPwCnzMGo9ClusccoL6ZRv15xyuodTTpvilDl8+cNJq/uQJLSrU1ZB/sjiOIzrDx29NZhf/YtEYfLv+0h35bVC1uX7evsSdGv5fF354Efw4Fpwh5vAHe4P7rBh4GrtXvVjHfUsYwd0R5vQHe2P7qhh6BrLB4Dqxzjd64gMEvlSoqhoFXxrX1CUOzrljqSo8FcWu1mp/sVFyVxP9dne2c0lH3m+Zae027aNu7aBe10IopqpvW5lp3stfYOfntfpPGkc5Lg+yuJ6uFtYPSu8x43Du1UXcBt8ELMLwyuH4+kmnncw29tkwkd84798uWDL3WA+iLIc64XBLoRwuy2Gh9pi+N1sscOB8Ckp4XZ8R4fiO2oivqUXON+ZI9YwxRq+uBNrrOGONQyyhkc+nE3+fThl89LuMlYYhmr3NLVnm6pqaZakmN84+azGbrtReXgnXtk42NX6hJiTHU4nzxf0cUNB38Awa5knN8I5Us57DhW/4AOI5hfcmNOZxh8s7gfwsHEAN/9wcT+ER41DuDkHjF9whTiKqraC8xbCmHd3qt1JqbokifdbbRtB/HKk35duNjm830n/OXI8OjVsFOh/i0PHRiH+dI8d8/C8fhjzfp8E+r4xibMxh4ibkf2wD7IfGoPs9zsv3Azl5T5QXjYGygYcDb6XkH6QdOxyE4vTpZgvxb5KtjY7iKXpT/mv2fyj/+HQP4d19Uh/bQ7ST/p8btYcnM/9SK5T/icBvJ7/N62X/wdQSwcIz7rzQucIAAD9SwAAUEsBAhQAFAAICAgAFXooRNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAVeihEz7rzQucIAAD9SwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAH4JAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /> | <ggb_applet width="649" height="515" version="4.2" ggbBase64="UEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAgIABV6KEQAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Vzdctu2Er5OnwLDi3MVSQT/ROVI6URqfpw4beY4p9M5NxmIhChEFMmSlH8yfZy+SV/sLACSIiVKlmRZodxqbIMgFljg28XuR9B2/8fbuY+uaZywMBgouK0qiAZO6LLAGyiLdNKylR9f/tD3aOjRcUzQJIznJB0oRltTlv2g1rZU3pm5A0WdTDSHqnbLwdhtGbo+aY1N3W1NyMRwbU3Hlu0oCN0m7EUQ/kzmNImIQ6+cKZ2Ty9AhqRhzmqbRi07n5uamnWtvh7HX8bxx+zZxFQQzD5KBkl28gOEqnW50Ia6pKu789vFSDt9iQZKSwKEK4qtasJc/POvfsMANb9ANc9PpQLHMroKmlHlTWKalwpo6XCiCtUbUSdk1TaBrqSrWnM4jRYiRgLc/k1fIL5ajIJddM5fGgE9bVw0DG6oqSwWFMaNBmkniTGMnH6t/zeiNHJRfCX3QKQ1Df0z4eOiPP5Cmaip6zgssCw0Ky5JNqryn6rLQZGHIwpQyhuxuSFFDyhhSxtDB2CxhY58OlAnxE8CPBZMYbFfUk/TOp2I+2Y3l2vFzWFPCvoGwzgGVgMN9VX3OvwHl50aOdGmRuKQ1jRdblcr2ks5co2X0dteoPWideq5Tq1ulZtbrtB+Gba4TmyWdoEp8ie91XK0tKiWQR9aobwN2VeNGU+6h0DJOvURD7XWPvsguBr/pahuVdtVT4Nrv5BGonwUdlEy5bLYpUzpPeBjSe8js8WiCkQkhx+pC8DAR7kHR1RAEGYRNZJhQxTayeNlFehcaDKQjG3E5rCMRc0wbfhhdMZiFTBiM3+1CqEMYFBnI1BEWocpAEKCQCHcQ+jQdJEwTmdCJq8caH0K3kGFBTbeRAXPkka6LQVCHjlAH9RrSMdJ5Z9xFmoUsPh42eAS1bD51GFJDlooszAeEYAmBUgZJkLeRzlcD2yoKE1agO6V+lIMkcGRBtEgr2DlzN79Mw6iwoZB2Q2c2LLDOWihJ0rIYpIllKpJpo5KpnvV9MqY+5PMr7ggIXROfRyqhYRIGKcqdQJP3vJhEU+YkVzRNoVeCvpJrcklSevsGpJNct1AtEmifLhyfuYwEv4KX8CH4gKjIpzz+5vnU0LtSixOGsXt1l4DroNv/0TiEoKkBgyh/IJzeySbdxtUmQDpxCHd6c6UTBJq7DU2WVE2vi6WRW1osCHkxK2zBry+SYei7RXMUsiAdkShdxIIcwexivqhXgedTga1IH0AznNk4vL2SoOpyrM93EdRUOYGxNwr9MEawJTXTBIGsHMtSyPCZFVKqkFGFhJpbiblFO+5pQkKUY1kKKTC7nFq2UpyvEqu5GpZIzqZU3Uw4DWcti4Cll3klZc4sWyqWHX5ezMfgbxlu1THxscbsd1ZcrD+jcUB96UgB2HIRLhLp2YV3PusvEvqJpNNXgfsf6sGe/ER4XExhaCm6nLJLHTaHjvJ+Bh7hhv0vTFXedakX03yJvuCjElrRqpbdeu22GOpNHM4vguvP4DUrU+138vX0EydmEXdONIZAPaNL/3NZQiDMu+V+sPgEVuHwiANAphxEBZFFOg1jQTlh2wLBQO//+jMIaAyBEtgm37E+nQPhRKlwS+HZhXleCR7L7YDC8VeII0XikO1L1KC51kWFMxM/mhLOdTMIfHIHEyiDIsb7GLqrUIElxHogNkTSJyJKpTvJ+cJFBMOJXVgyt8A+QbcDpaXxR5E7/lwC5Tf5XCNZPF8q35qVMCjvrlgNnE6idA9ew/PHC58QrtH5w6VmcGlHgssJ53MSuCgQrO1T6N95YaAs+QJR+a5EBHNnQ0TjIEqEFmneDnHRh8SDpZgjxQgU+kAZS4WZmhr7SIW5BYqhqhkkBVIwgwfSRKS5NEto4uIdc10qKE9nu3FLcJati01d2NfEWYpbmhfvY97NPphQj9eKiTj3eOH+E93TD9e9Sc+8qYW1YrADwAef8LnvXgQ80VGRGtZT44zSiHOSX4LPMQkSfqpTzYm7Q0maA2Ue9ls4w/K8kBw3B8kig7byIGc0GspqjvlpHcgqBT2DJKOfMCe/Pi1ev0wmCU0F8bBkItVOhSY+AZpvnoD3mStJ6RQU5yfJXV5L7vJmE8XRpNhEirmS4tCDKI52HIpTtW5jOM7kPj88YT7J95+ak5xeo9PJKpRug6AsUvN5ZOZVKGmToMSrLAfjRoNZTTRvn0CiyZ3ZPEFifveE8FLb9iMk5ktw+pWs/Fam23dr6djbnnL5/imA9Q7c9NWD7yPsePFrC+U8ZLeNw/c7/T2QXRJ5fs3mkc8clu7jlBdPwCnzMGo9ClusccoL6ZRv15xyuodTTpvilDl8+cNJq/uQJLSrU1ZB/sjiOIzrDx29NZhf/YtEYfLv+0h35bVC1uX7evsSdGv5fF354Efw4Fpwh5vAHe4P7rBh4GrtXvVjHfUsYwd0R5vQHe2P7qhh6BrLB4Dqxzjd64gMEvlSoqhoFXxrX1CUOzrljqSo8FcWu1mp/sVFyVxP9dne2c0lH3m+Zae027aNu7aBe10IopqpvW5lp3stfYOfntfpPGkc5Lg+yuJ6uFtYPSu8x43Du1UXcBt8ELMLwyuH4+kmnncw29tkwkd84798uWDL3WA+iLIc64XBLoRwuy2Gh9pi+N1sscOB8Ckp4XZ8R4fiO2oivqUXON+ZI9YwxRq+uBNrrOGONQyyhkc+nE3+fThl89LuMlYYhmr3NLVnm6pqaZakmN84+azGbrtReXgnXtk42NX6hJiTHU4nzxf0cUNB38Awa5knN8I5Us57DhW/4AOI5hfcmNOZxh8s7gfwsHEAN/9wcT+ER41DuDkHjF9whTiKqraC8xbCmHd3qt1JqbokifdbbRtB/HKk35duNjm830n/OXI8OjVsFOh/i0PHRiH+dI8d8/C8fhjzfp8E+r4xibMxh4ibkf2wD7IfGoPs9zsv3Azl5T5QXjYGygYcDb6XkH6QdOxyE4vTpZgvxb5KtjY7iKXpT/mv2fyj/+HQP4d19Uh/bQ7ST/p8btYcnM/9SK5T/icBvJ7/N62X/wdQSwcIz7rzQucIAAD9SwAAUEsBAhQAFAAICAgAFXooRNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgICAAVeihEz7rzQucIAAD9SwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAH4JAAAAAA==" showResetIcon = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /> | ||
| − | + | <br /> | |
| − | + | [[Datei:Aufgabe 10.1 WS 18 19.png|400px]]<br /> | |
| + | Konstruieren der Mittelsenkrechten von <math>\overline{BB''}</math> und <math>\overline{CC''}</math> um den Drehpunkt M zu ermitteln. Die Mittelsenkrechte von <math>\overline{BB''}</math> ist gleichzeitig Winkelhalbierende des Winkels <(BMB'') und kann als eine Spiegelgerade genutzt werden. Da B dadurch schon korrekt auf B'' gespiegelt wird, ist eine mögliche andere Spiegelgeraden BM, da B dort Fixpunkt ist. In diesem Fall muss zuerst an BM, dann an der Mittelsenkrechten von <math>\overline{BB''}</math> gespiegelt werden.--[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:14, 20. Dez. 2018 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 20. Dezember 2018, 21:15 Uhr
Das Dreieck 
wurde durch die Nacheinanderausführung zweier verschiedener Geradenspiegelungen auf das Dreieck 
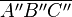abgebildet. Konstruieren Sie die beiden Spiegelgeraden.
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren
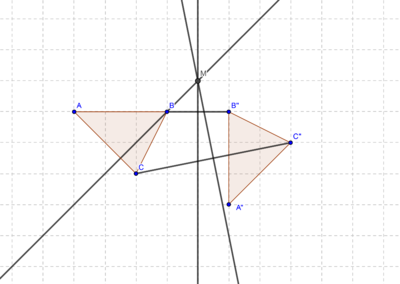
Konstruieren der Mittelsenkrechten von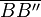 
und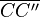 
um den Drehpunkt M zu ermitteln. Die Mittelsenkrechte von 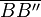ist gleichzeitig Winkelhalbierende des Winkels <(BMB) und kann als eine Spiegelgerade genutzt werden. Da B dadurch schon korrekt auf B gespiegelt wird, ist eine mögliche andere Spiegelgeraden BM, da B dort Fixpunkt ist. In diesem Fall muss zuerst an BM, dann an der Mittelsenkrechten von 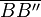gespiegelt werden.--CIG UA (Diskussion) 21:14, 20. Dez. 2018 (CET)
