Lösung von Aufgabe 12.6: Unterschied zwischen den Versionen
(→Versuch 1) |
(→Versuch 1) |
||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 22: | Zeile 22: | ||
|- | |- | ||
! style="background: #FFDDDD;"|(III) | ! style="background: #FFDDDD;"|(III) | ||
| − | | das Maß von <math> | \angle PQR| = \alpha </math> im Punkt <math>\ P </math> an Gerade <math>\ PQ </math>, am Strahl <math>\ { | + | | das Maß von <math> | \angle PQR| = \alpha </math> im Punkt <math>\ P </math> an Gerade <math>\ PQ </math>, am Strahl <math>\ {PQ^{-}}</math> in der Halbebene <math>\ {PQ,R^{+}}</math> abtragen. Es exisitert genau ein <math>\ {PS^{+}}</math> mit dem Maß <math>\ |\alpha{'}| = | \alpha| </math> |
| (Winkelkonstruktionsaxiom), (Winkelmaßaxiom), (I), (II) | | (Winkelkonstruktionsaxiom), (Winkelmaßaxiom), (I), (II) | ||
|- | |- | ||
Aktuelle Version vom 17. Juli 2010, 12:51 Uhr
Beweisen Sie: Wenn  ein Punkt außerhalb der Geraden
ein Punkt außerhalb der Geraden  ist, dann gibt es eine Gerade
ist, dann gibt es eine Gerade  , die durch
, die durch  geht und parellel zu
geht und parellel zu  ist.
ist.
Versuch 1
VSS: Punkt  , Gerade
, Gerade  ,
, 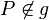
Beh: Gerade  ,
, 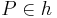 ,
, 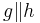
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 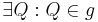 , , 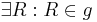
|
(Axiom I.0) |
| (II) | Gerade 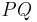
|
(Axiom I.1) |
| (III) | das Maß von 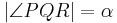 im Punkt im Punkt  an Gerade an Gerade 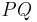 , am Strahl , am Strahl 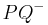 in der Halbebene in der Halbebene 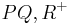 abtragen. Es exisitert genau ein abtragen. Es exisitert genau ein 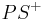 mit dem Maß mit dem Maß 
|
(Winkelkonstruktionsaxiom), (Winkelmaßaxiom), (I), (II) |
| (IV) | 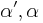 sind Stufenwinkel sind Stufenwinkel
|
(III), (Def. Stufenwinkel) |
| (V) | 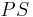 = = 
|
(Axiom I.1) |
| (V) | 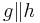
|
(Umkehrung Stufenwinkelsatz), (IV), (V) |
--> Beh ist wahr.
--Löwenzahn 11:07, 14. Jul. 2010 (UTC)
Versuch 2
Mal wieder formlos: folgender Vorschlag:
Zu beweisen sind Existenz und Eindeutigkeit.
Die Gerade h, die durch den Punkt P geht kann sich zu g auf drei Arten verhalten:
- Fall: ist identisch => Widerspruch zur Voraussetzung
- Fall: schneidet h
- Fall: ist parallel zu h, also schnittpunktfrei
Fall 2 und 3 sind laut Vor. möglich, also existiert auf jeden Fall eine parallele Gerade.
Die Eindeutigkeit beweise ich indirekt.
Annahme: Es gibt genau zwei Parallelen durch P, die zu g parallel stehen, nämlich h und i, die nicht identisch sind.
(1) P ist sowohl Element von h, als auch von i. Die Geraden h und i sind damit identisch (Widerspruch Annahme) oder P ist ihr Schnittpunkt. Damit sind i und h aber nicht zueinander parallel (da nicht schnittpunktfrei). Parallelität ist transitiv. Wenn h und i nicht parallel sind, dann gilt entweder h parallel zu g oder i parallel zu g. Damit gibt es wieder nur eine Gerade durch P, die zu g parallel ist und nicht zwei.
--Nicola 15:49, 14. Jul. 2010 (UTC)

