Lösung von Aufgabe 12.3P (WS 18/19): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \r…“) |
CIG UA (Diskussion | Beiträge) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | Zeigen Sie, dass die Verkettung einer Drehung <math>D_{\left( S,\alpha \right) } </math> mit einer Verschiebung wieder eine Drehung <math>D_{\left( P,\alpha \right) } </math> ergibt. Wo liegt das neue Drehzentrum ''P''? | ||
| + | <br /> | ||
<br /> | <br /> | ||
| + | D<sub>(S,α)</sub><math>\circ</math>S<sub>c</sub><math>\circ</math>S<sub>d</sub> = S<sub>a</sub><math>\circ</math>S<sub>b</sub><math>\circ</math>S<sub>c</sub><math>\circ</math>S<sub>d</sub> mit Betrag orientierter Winkel (ab) = |1/2 α| und c || d und a geschnitten b = {S}<br /> | ||
| + | = S<sub>a'</sub><math>\circ</math>S<sub>b'</sub><math>\circ</math>S<sub>c</sub><math>\circ</math>S<sub>d</sub> mit Betrag orientierter Winkel (a'b') = |1/2 α| und a' geschnitten b' = {S} und b' || c<br /> | ||
| + | = S<sub>a'</sub><math>\circ</math>S<sub>b'</sub><math>\circ</math>S<sub>c'</sub><math>\circ</math>S<sub>d'</sub> mit b' = c' und |cd| = |c'd'|<br /> | ||
| + | = S<sub>a'</sub><math>\circ</math>S<sub>d'</sub> mit Betrag orientierter Winkel (a'd') = |1/2 α|<br /> | ||
| + | = D<sub>(P,α)</sub> mit {P} = a' geschnitten d'<br /> | ||
| + | --[[Benutzer:CIG UA|CIG UA]] ([[Benutzer Diskussion:CIG UA|Diskussion]]) 21:13, 16. Jan. 2019 (CET) | ||
[[Kategorie:Geo_P]] | [[Kategorie:Geo_P]] | ||
Aktuelle Version vom 29. Januar 2019, 21:01 Uhr
Zeigen Sie, dass die Verkettung einer Drehung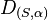 
mit einer Verschiebung wieder eine Drehung 
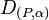ergibt. Wo liegt das neue Drehzentrum P?
D(S,α)
ScSd = SaSbScSd mit Betrag orientierter Winkel (ab) = |1/2 α| und c || d und a geschnitten b = {S}
= Sa'Sb'ScSd mit Betrag orientierter Winkel (a'b') = |1/2 α| und a' geschnitten b' = {S} und b' || c
= Sa'Sb'Sc'Sd' mit b' = c' und |cd| = |c'd'|
= Sa'Sd' mit Betrag orientierter Winkel (a'd') = |1/2 α|
= D(P,α) mit {P} = a' geschnitten d'
--CIG UA (Diskussion) 21:13, 16. Jan. 2019 (CET)
