Serie 1 Geradengleichungen in der Ebene: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 9) |
||
| (8 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
# <math>P=A+t\vec{r}</math> | # <math>P=A+t\vec{r}</math> | ||
. | . | ||
| + | =Aufgabe 2= | ||
| + | Die Gerade <math>g</math> möge die <math>x-</math>Achse unter einem Winkel von <math>30^\circ</math> im Punkt <math>A\left(\sqrt{2}, 0\right)</math> schneiden. | ||
| + | # Zeichnen Sie ein kartesisches Koordinatensystem auf ein Blatt Papier. Konstruieren Sie nur mit Zirkel und Lineal eine grafische Darstellung der Geraden <math>g</math> bezüglich Ihres Koordinatensystems. | ||
| + | # Geben Sie eine Gleichung der Form <math>y=mx+n</math> zur Beschreibung von <math>g</math> an. | ||
| + | # Geben Sie eine Gleichung der Form <math>ax+by+c=0</math> zur Beschreibung von <math>g</math> an. | ||
| + | # Geben Sie eine Gleichung der Form <math>P=A+t\vec{r}</math>zur Beschreibung von <math>g</math> an. | ||
| + | |||
| + | =Aufgabe 3= | ||
| + | Eine Gerade <math>g</math> habe ein Anstiegsdreieck, dessen zur <math>y-</math> Achse parallele Kathete die Länge <math>\Delta y</math> hat. Die andere Kathete möge die Länge <math>\Delta x</math> haben. Geben sie fünf Vektoren <math>\overrightarrow{n_1}, \overrightarrow{n_2}, \overrightarrow{n_3}, \overrightarrow{n_4}, \overrightarrow{n_5}</math> an, die bezüglich <math>g</math> Normalenvektoren sind. Einer dieser Vektoren möge die Länge <math>1</math> haben, d.h. ein Normaleneinheitsvektor sein. | ||
| + | =Aufgabe 4= | ||
| + | Zeichnen Sie auf ein Blatt Papier ein kartesisches Koordinatensystem. | ||
| + | # Zeichen Sie bezüglich dieses Koordinatensystems die Gerade <math>g</math> ein, die durch die Gleichung <math>y=\frac{3}{5}x</math> beschrieben wird. | ||
| + | # Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade <math>h</math> ein, die durch die Gleichung <math>\frac{3}{5}x-\frac{4}{5}=0</math> beschrieben wird. | ||
| + | # Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade <math>i</math> ein, die durch die Gleichung <math>-3x+4y=0</math> beschrieben wird. | ||
| + | # Interpretieren Sie die Gleichungen für <math>h</math> und <math>i</math> als <math>ax+by=0</math>. Zeichnen Sie für beide Geraden jeweils die Vektoren <math>\begin{pmatrix} a \\ b \end{pmatrix}</math> ein. | ||
| + | # Zeichnen Sie den Punkt <math>P\left(10, \frac{10}{8} \right)</math> ein. Messen Sie den Abstand von <math>P</math> zu <math>g</math>. | ||
| + | # Berechnen Sie <math>\frac{3}{5}10-\frac{4}{5}\frac{10}{8}=d</math>. Was stellen Sie fest? | ||
| + | =Aufgabe 5= | ||
| + | Gegeben sei die Funktion <math>f</math> mittels der Gleichung <math>f(x)=\frac{3}{2}x^2+1</math>. Beschreiben Sie die Tangente <math>t</math> an <math>f</math> im Punkt <math>B(2, f(2)</math> durch Gleichungen der Form | ||
| + | # <math>y=mx+n</math> | ||
| + | # <math>ax+by+c=0</math> | ||
| + | # <math>P=A+t\vec{r}</math> | ||
| + | =Aufgabe 6= | ||
| + | Im <math>\mathbb{R}^3</math> sei ein Würfel <math>W</math> mit der Kantenlänge <math>1</math>gegeben. Die Grundfläche von <math>W</math> sei das Quadrat <math>\overline{ABCD}</math>, wobei <math>A</math> auf der positiven <math>x-</math>Achse, <math>B</math> auf der positiven <math>y-</math>Achse, <math>C</math> auf der negativen <math>x-</math>Achse und <math>D</math> auf der negativen <math>y-</math>Achse liegen mögen. Die Deckfläche von <math>W</math> erhalten wir durch Verschiebung der Grundfläche längs des Vektors <math>\overrightarrow{v} = \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix}</math>. Der Punkt <math>A</math> wird bei dieser Verschiebung auf den Punkt <math>E</math> abgebildet, desweiteren <math>B</math> auf <math>F</math>, <math>C</math> auf <math>G</math> und schließlich <math>D</math> auf den Punkt <math>H</math>.<br /> | ||
| + | <math>W</math> Wird jetzt einer Drehung mit dem Drehwinkel <math>45^\circ</math> um die <math>z-</math>Achse unterworfen. Geben Sie für die Raumdiagonalen des gedrehten Würfels jeweils eine Parameterdarstellung an, wobei die Richtungsvektoren jeweils Einheitsvektoren sein mögen. | ||
| + | =Aufgabe 7= | ||
| + | In der <math>x-z-</math>Ebene des <math>\mathbb{R}^3</math> sei die Funktion <math>f</math> mit <math>z(x)=-x^2+10</math> gegeben. Wir erzeugen mittels Rotation um die <math>z-</math>Achse aus <math>f</math> ein Drehparaboloid <math>P</math>. <math>\varepsilon</math> sei die Ebene, die man erhält, wenn man die <math>y-z-</math>Ebene um <math>30^\circ</math> um die <math>z-</math>Achse dreht. Der Schnitt von <math>\varepsilon</math> mit <math>P</math> ist eine Parabel <math>p</math>. Geben Sie jeweils eine Parameterdarstellung für die beiden Tangenten an <math>p</math> an, die in <math>\varepsilon</math> liegen und deren Berührungspunkte jeweils den Abstand <math>2</math> zur <math>z-</math>Achse haben. | ||
| + | =Aufgabe 8= | ||
| + | Die Ebene <math>\varepsilon</math> möge das Koordinatensystem in den Punkten <math>A\begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix}, B\begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix}, C=\begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} </math> schneiden. Geben Sie eine Gleichung der Form <math>ax+by+cz+d=0</math> zur Beschreibung von <math>\varepsilon</math> an. | ||
| + | =Aufgabe 9= | ||
| + | Informieren Sie sich, wie man den Schwerpunkt eines Dreiecks berechnet. Berechnen Sie den Schwerpunkt <math>S</math> des Dreiecks <math>\overline{ABC}</math> aus Aufgabe 8. Lassen Sie das Dreieck mit Geogebra 3D zeichnen und lassen sie ebenso den Schwerpunkt <math>S</math> einzeichnen. Welche Lage hat der Ortsvektor von <math>S</math> bezüglich der Ebene <math>\varepsilon</math>? | ||
| + | |||
| + | =Aufgabe 10= | ||
| + | Berechnen Sie die Länge des Ortsvektors von <math>S</math> aus Aufgabe 9. | ||
Aktuelle Version vom 2. Mai 2019, 17:23 Uhr
Inhaltsverzeichnis |
Aufgabe 1
Gegeben seien die Punkte 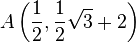 und
und 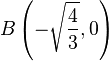 .
.
Beschreiben Sie die Gerade  jeweils durch eine Gleichung der Form
jeweils durch eine Gleichung der Form
.
Aufgabe 2
Die Gerade  möge die
möge die 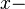 Achse unter einem Winkel von
Achse unter einem Winkel von 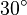 im Punkt
im Punkt 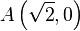 schneiden.
schneiden.
- Zeichnen Sie ein kartesisches Koordinatensystem auf ein Blatt Papier. Konstruieren Sie nur mit Zirkel und Lineal eine grafische Darstellung der Geraden
 bezüglich Ihres Koordinatensystems.
bezüglich Ihres Koordinatensystems.
- Geben Sie eine Gleichung der Form
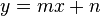 zur Beschreibung von
zur Beschreibung von  an.
an.
- Geben Sie eine Gleichung der Form
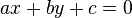 zur Beschreibung von
zur Beschreibung von  an.
an.
- Geben Sie eine Gleichung der Form
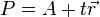 zur Beschreibung von
zur Beschreibung von  an.
an.
Aufgabe 3
Eine Gerade  habe ein Anstiegsdreieck, dessen zur
habe ein Anstiegsdreieck, dessen zur 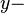 Achse parallele Kathete die Länge
Achse parallele Kathete die Länge 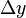 hat. Die andere Kathete möge die Länge
hat. Die andere Kathete möge die Länge 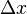 haben. Geben sie fünf Vektoren
haben. Geben sie fünf Vektoren 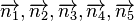 an, die bezüglich
an, die bezüglich  Normalenvektoren sind. Einer dieser Vektoren möge die Länge
Normalenvektoren sind. Einer dieser Vektoren möge die Länge 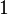 haben, d.h. ein Normaleneinheitsvektor sein.
haben, d.h. ein Normaleneinheitsvektor sein.
Aufgabe 4
Zeichnen Sie auf ein Blatt Papier ein kartesisches Koordinatensystem.
- Zeichen Sie bezüglich dieses Koordinatensystems die Gerade
 ein, die durch die Gleichung
ein, die durch die Gleichung 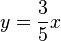 beschrieben wird.
beschrieben wird.
- Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade
 ein, die durch die Gleichung
ein, die durch die Gleichung 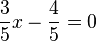 beschrieben wird.
beschrieben wird.
- Zeichnen Sie bezüglich dieses Koordinatensystems die Gerade
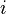 ein, die durch die Gleichung
ein, die durch die Gleichung 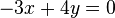 beschrieben wird.
beschrieben wird.
- Interpretieren Sie die Gleichungen für
 und
und 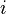 als
als 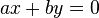 . Zeichnen Sie für beide Geraden jeweils die Vektoren
. Zeichnen Sie für beide Geraden jeweils die Vektoren 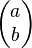 ein.
ein.
- Zeichnen Sie den Punkt
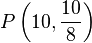 ein. Messen Sie den Abstand von
ein. Messen Sie den Abstand von  zu
zu  .
.
- Berechnen Sie
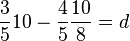 . Was stellen Sie fest?
. Was stellen Sie fest?
Aufgabe 5
Gegeben sei die Funktion  mittels der Gleichung
mittels der Gleichung 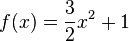 . Beschreiben Sie die Tangente
. Beschreiben Sie die Tangente  an
an  im Punkt
im Punkt 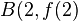 durch Gleichungen der Form
durch Gleichungen der Form
Aufgabe 6
Im 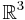 sei ein Würfel
sei ein Würfel 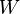 mit der Kantenlänge
mit der Kantenlänge 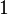 gegeben. Die Grundfläche von
gegeben. Die Grundfläche von 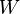 sei das Quadrat
sei das Quadrat  , wobei
, wobei  auf der positiven
auf der positiven 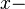 Achse,
Achse,  auf der positiven
auf der positiven 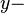 Achse,
Achse,  auf der negativen
auf der negativen 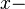 Achse und
Achse und  auf der negativen
auf der negativen 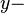 Achse liegen mögen. Die Deckfläche von
Achse liegen mögen. Die Deckfläche von 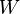 erhalten wir durch Verschiebung der Grundfläche längs des Vektors
erhalten wir durch Verschiebung der Grundfläche längs des Vektors 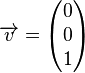 . Der Punkt
. Der Punkt  wird bei dieser Verschiebung auf den Punkt
wird bei dieser Verschiebung auf den Punkt  abgebildet, desweiteren
abgebildet, desweiteren  auf
auf  ,
,  auf
auf  und schließlich
und schließlich  auf den Punkt
auf den Punkt 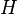 .
.
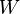 Wird jetzt einer Drehung mit dem Drehwinkel
Wird jetzt einer Drehung mit dem Drehwinkel 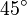 um die
um die 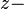 Achse unterworfen. Geben Sie für die Raumdiagonalen des gedrehten Würfels jeweils eine Parameterdarstellung an, wobei die Richtungsvektoren jeweils Einheitsvektoren sein mögen.
Achse unterworfen. Geben Sie für die Raumdiagonalen des gedrehten Würfels jeweils eine Parameterdarstellung an, wobei die Richtungsvektoren jeweils Einheitsvektoren sein mögen.
Aufgabe 7
In der 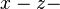 Ebene des
Ebene des 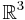 sei die Funktion
sei die Funktion  mit
mit 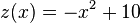 gegeben. Wir erzeugen mittels Rotation um die
gegeben. Wir erzeugen mittels Rotation um die 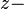 Achse aus
Achse aus  ein Drehparaboloid
ein Drehparaboloid  .
.  sei die Ebene, die man erhält, wenn man die
sei die Ebene, die man erhält, wenn man die 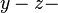 Ebene um
Ebene um 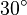 um die
um die 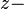 Achse dreht. Der Schnitt von
Achse dreht. Der Schnitt von  mit
mit  ist eine Parabel
ist eine Parabel  . Geben Sie jeweils eine Parameterdarstellung für die beiden Tangenten an
. Geben Sie jeweils eine Parameterdarstellung für die beiden Tangenten an  an, die in
an, die in  liegen und deren Berührungspunkte jeweils den Abstand
liegen und deren Berührungspunkte jeweils den Abstand 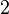 zur
zur 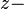 Achse haben.
Achse haben.
Aufgabe 8
Die Ebene  möge das Koordinatensystem in den Punkten
möge das Koordinatensystem in den Punkten 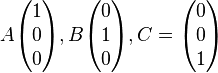 schneiden. Geben Sie eine Gleichung der Form
schneiden. Geben Sie eine Gleichung der Form 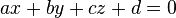 zur Beschreibung von
zur Beschreibung von  an.
an.
Aufgabe 9
Informieren Sie sich, wie man den Schwerpunkt eines Dreiecks berechnet. Berechnen Sie den Schwerpunkt  des Dreiecks
des Dreiecks  aus Aufgabe 8. Lassen Sie das Dreieck mit Geogebra 3D zeichnen und lassen sie ebenso den Schwerpunkt
aus Aufgabe 8. Lassen Sie das Dreieck mit Geogebra 3D zeichnen und lassen sie ebenso den Schwerpunkt  einzeichnen. Welche Lage hat der Ortsvektor von
einzeichnen. Welche Lage hat der Ortsvektor von  bezüglich der Ebene
bezüglich der Ebene  ?
?
Aufgabe 10
Berechnen Sie die Länge des Ortsvektors von  aus Aufgabe 9.
aus Aufgabe 9.

