Diskussion:Lösung von Aufgabe 13.5: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: Zur Lösung von Löwenzahn: ::Muss es nicht heißen <math> \alpha \equiv \angle ASB \equiv \angle pq </math>? Aber mal wieder nur Haarspalterei, vermutlich. ::Und: bra...) |
|||
| (11 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 6: | Zeile 6: | ||
::Besser vielleicht: <math>| \angle ASP| + \angle BSP|= |\angle ASB| \rightarrow |\angle ASP| + | \angle ASP| =|\angle ASB| </math> | ::Besser vielleicht: <math>| \angle ASP| + \angle BSP|= |\angle ASB| \rightarrow |\angle ASP| + | \angle ASP| =|\angle ASB| </math> | ||
<br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 16:18, 20. Jul. 2010 (UTC) | <br />--[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 16:18, 20. Jul. 2010 (UTC) | ||
| + | |||
| + | Kommentar --[[Benutzer:Löwenzahn|Löwenzahn]] 16:42, 20. Jul. 2010 (UTC): | ||
| + | # Deinen ersten Punkt verstehen ich nicht [[Benutzer:Heinzvaneugen|Heinzvaneugen]]... ist das nicht das gleiche, ob ich nun drei Striche, oder einen davon geschwungen mache??? | ||
| + | # Ich habe versucht über SSW zu argumentrieren, und da muss doch vorher gezeigt werden, dass der größere Winkel, der größeren Seite etc... geht der Satz auch über SWS? | ||
| + | # Ich habe mit "<math>| \angle ASP| + \angle BSP|= |\angle ASB| \rightarrow |\angle ASP| + | \angle ASP| =|\angle ASB| </math>" auch gezeigt, dass <math> {SP^{+}} </math> im Inneren liegt, oder?! | ||
| + | |||
| + | Re: --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 23:03, 20. Jul. 2010 (UTC) | ||
| + | |||
| + | # Die Identität ist was anderes als die Kongruenz. Zwei Winkel die kongruent sind, müssen noch lange nicht identisch sein. Du willst einen bestimmten Winkel definieren, also sagst du, dass die Bezeichnungen Analogien sind, also wir nicht von kongruenten Winkeln sprechen z.B. dem Winkel <math>\ \alpha</math> und <math>\ \alpha'</math> sondern, dass <math>\ \alpha</math> und der Winkel <math>\ \angle BAC</math> identisch sind. | ||
| + | # Das ist sicher auch möglich, schöne Argumentation sicherlich. Ich wollte nicht nutzlos rummäkeln, sondern nur eine "einfachere" Strategie vorschlagen. | ||
| + | # Das hast Du sicher gezeigt, aber nur weil die beiden Winkel sich zu einem Winkel aufaddieren, sind sie noch lange nicht kongruent oder haben als gemeinsamen Strahl die Winkelhalbierende, deshalb diese Umformung. | ||
| + | |||
| + | Re: --[[Benutzer:Löwenzahn|Löwenzahn]] 09:06, 21. Jul. 2010 (UTC) | ||
| + | # ok... verstehe... hast du denn den Beweis auch über SWS führen können? | ||
| + | |||
| + | Re: D'OH!! --[[Benutzer:Heinzvaneugen|Heinzvaneugen]] 12:09, 21. Jul. 2010 (UTC) | ||
| + | # Schon besprochen... | ||
| + | # Schon bei meinem letzten Reply war ich mir nicht ganz sicher, jetzt habe ich durch Deinen letzten Reply entdeckt, wo mein Fehler liegt: Ich hatte die Punkte anders bezeichnet und da kam natürlich was anderes bei raus. Es geht NUR über SSW, davon bin ich nun auch überzeugt. Mit meiner tiefsten Huldigung verbunden ziehe ich meine ursprüngliche Behauptung zurück und behaupte nunmehr das Gegenteil ;-) | ||
| + | # Schon besprochen... | ||
| + | |||
| + | Darf ich den SSW einfach so benutzen. Müsste ich nicht erst noch zeigen, dass dieser Satz gilt. Denn so weit ich mich erinnern kann, haben wir ihn noch nicht bewiesen.--[[Benutzer:Frühling|Frühling]] 15:44, 25. Jul. 2010 (UTC) | ||
| + | |||
| + | Genau genommen hast du recht, man müsste ihn erst beweisen. Wir können aber (so weit ich weiß)die Dreieckskongruenzsätze als gegeben ansehen.--[[Benutzer:Löwenzahn|Löwenzahn]] 17:43, 25. Jul. 2010 (UTC) | ||
| + | |||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 16. November 2010, 22:12 Uhr
Zur Lösung von Löwenzahn:
- Muss es nicht heißen
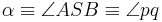 ? Aber mal wieder nur Haarspalterei, vermutlich.
? Aber mal wieder nur Haarspalterei, vermutlich.
- Und: braucht man Schritt (V) bis (VII). Es reicht doch die Dreieckskongruenz aus, die man aus SWS und (II), (III) und (IV) ableiten kann.
- Und: Du meinst in Schritt (X) sicher das Richtige, nur fehlt die Form, aus der abzusehen ist, dass
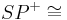 Winkelhalbierenden von
Winkelhalbierenden von 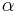 .
.
- "Es seien
 ,
,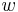 und
und 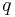 drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt
drei Halbgeraden ein und derselben Ebene mit dem gemeinsamen Anfangspunkt  . Die Halbgerade
. Die Halbgerade 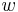 ist die Winkelhalbierende des Winkels
ist die Winkelhalbierende des Winkels 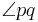 , wenn
, wenn 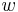 im Inneren von
im Inneren von 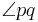 liegt und die beiden Winkel
liegt und die beiden Winkel 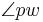 und
und 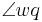 dieselbe Größe haben."
dieselbe Größe haben."
- Besser vielleicht:
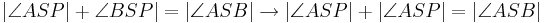
- Muss es nicht heißen
--Heinzvaneugen 16:18, 20. Jul. 2010 (UTC)
Kommentar --Löwenzahn 16:42, 20. Jul. 2010 (UTC):
- Deinen ersten Punkt verstehen ich nicht Heinzvaneugen... ist das nicht das gleiche, ob ich nun drei Striche, oder einen davon geschwungen mache???
- Ich habe versucht über SSW zu argumentrieren, und da muss doch vorher gezeigt werden, dass der größere Winkel, der größeren Seite etc... geht der Satz auch über SWS?
- Ich habe mit "
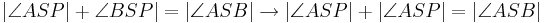 " auch gezeigt, dass
" auch gezeigt, dass 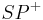 im Inneren liegt, oder?!
im Inneren liegt, oder?!
Re: --Heinzvaneugen 23:03, 20. Jul. 2010 (UTC)
- Die Identität ist was anderes als die Kongruenz. Zwei Winkel die kongruent sind, müssen noch lange nicht identisch sein. Du willst einen bestimmten Winkel definieren, also sagst du, dass die Bezeichnungen Analogien sind, also wir nicht von kongruenten Winkeln sprechen z.B. dem Winkel
 und
und 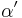 sondern, dass
sondern, dass  und der Winkel
und der Winkel 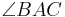 identisch sind.
identisch sind.
- Das ist sicher auch möglich, schöne Argumentation sicherlich. Ich wollte nicht nutzlos rummäkeln, sondern nur eine "einfachere" Strategie vorschlagen.
- Das hast Du sicher gezeigt, aber nur weil die beiden Winkel sich zu einem Winkel aufaddieren, sind sie noch lange nicht kongruent oder haben als gemeinsamen Strahl die Winkelhalbierende, deshalb diese Umformung.
Re: --Löwenzahn 09:06, 21. Jul. 2010 (UTC)
- ok... verstehe... hast du denn den Beweis auch über SWS führen können?
Re: D'OH!! --Heinzvaneugen 12:09, 21. Jul. 2010 (UTC)
- Schon besprochen...
- Schon bei meinem letzten Reply war ich mir nicht ganz sicher, jetzt habe ich durch Deinen letzten Reply entdeckt, wo mein Fehler liegt: Ich hatte die Punkte anders bezeichnet und da kam natürlich was anderes bei raus. Es geht NUR über SSW, davon bin ich nun auch überzeugt. Mit meiner tiefsten Huldigung verbunden ziehe ich meine ursprüngliche Behauptung zurück und behaupte nunmehr das Gegenteil ;-)
- Schon besprochen...
Darf ich den SSW einfach so benutzen. Müsste ich nicht erst noch zeigen, dass dieser Satz gilt. Denn so weit ich mich erinnern kann, haben wir ihn noch nicht bewiesen.--Frühling 15:44, 25. Jul. 2010 (UTC)
Genau genommen hast du recht, man müsste ihn erst beweisen. Wir können aber (so weit ich weiß)die Dreieckskongruenzsätze als gegeben ansehen.--Löwenzahn 17:43, 25. Jul. 2010 (UTC)

