Lösung von Aufgabe 13.5
Man beweise: Ein Punkt  gehört genau dann zur Winkelhalbierenden des Winkels
gehört genau dann zur Winkelhalbierenden des Winkels  , wenn er zu den Schenkeln von
, wenn er zu den Schenkeln von  jeweils denselben Abstand hat.
jeweils denselben Abstand hat.
Versuch 1
Da es sich bei diesem Satz um eine Äquivalenzrelation handelt ("genau dann") muss die "Hin- und Rückrichtung" bewiesen werden.
1. Hinrichtung: "Wenn ein Punkt P zu den Schenkeln von  jeweils denselben Abstand hat, dann gehört er zur Winkelhalbierenden des Winkels
jeweils denselben Abstand hat, dann gehört er zur Winkelhalbierenden des Winkels  ."
."
VSS: 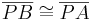 ,
, 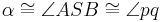
Beh: 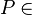 Winkelhalbierende von
Winkelhalbierende von 
Kommentar --Heinzvaneugen 16:18, 20. Jul. 2010 (UTC): siehe Diskussion
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) |  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl  und und  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl 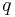
|
(Existenz und Eindeutigkeit Lot) |
| (II) | 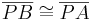
|
(VSS) |
| (III) | 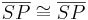
|
(trivial) |
| (IV) | 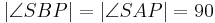
|
(Definition Lot) |
| (V) | 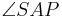 ist größter Winkel im Dreieck ist größter Winkel im Dreieck 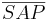
|
(Satz: höchstens ein rechter Winkel im Dreieck), (IV) |
| (VI) | 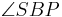 ist größter Winkel im Dreieck ist größter Winkel im Dreieck 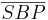
|
(Satz: höchstens ein rechter Winkel im Dreieck), (IV) |
| (VII) | 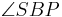 liegt der Seite liegt der Seite  gegenüber gegenüber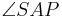 liegt der Seite liegt der Seite  gegenüber gegenüber
|
(Satz: größter Winkel liegt längsten Seite gegenüber),(V), (VI) |
| (VIII) | 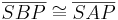
|
(SSW), (VII), (IV), (III), (II) |
| (IX) | 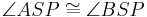
|
(VIII), (Def. Dreieckskongruenz) |
| (X) | 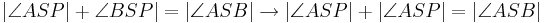
|
(IX), (Def. Winkelhalbierende), (Winkeladditionsaxiom) |
| (XI) | 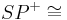 Winkelhalbierenden von Winkelhalbierenden von 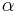 --> --> 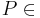 Winkelhalbierende von Winkelhalbierende von 
|
(X) |
--> Beh. wahr qed
2. Rückrichtung: "Wenn ein Punkt  zur Winkelhalbierenden des Winkels
zur Winkelhalbierenden des Winkels  gehört, dann hat er zu den Schenkeln von
gehört, dann hat er zu den Schenkeln von  jeweils denselben Abstand."
jeweils denselben Abstand."
VSS: 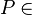 Winkelhalbierende von
Winkelhalbierende von  und
und 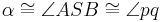
Beh: 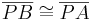
| Nr. | Beweisschritt | Begründung |
|---|---|---|
| (I) | 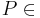 Winkelhalbierende von Winkelhalbierende von 
|
(VSS) |
| (II) |  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl  und und  sei der Lotfußpunkt von sei der Lotfußpunkt von  auf den Strahl auf den Strahl 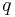
|
(Existenz und Eindeutigkeit des Lotes) |
| (III) | 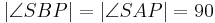
|
(II), (Def. Lot) |
| (IV) | 
|
(Def. Winkelhalbierende) |
| (V) | 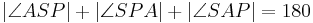
|
(Innenwinkelsumme im Dreieck) |
| (VI) | 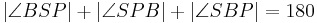
|
(Innenwinkelsumme im Dreieck) |
| (VII) | 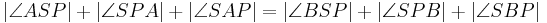
|
(V), (VI), (rechnen mit reellen Zahlen) |
| (VIII) | 
|
(VII), (IV), (rechnen mit reellen Zahlen) |
| (IX) | 
|
(IX), (III), (rechnen mit reellen Zahlen) |
| (X) | 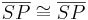
|
(trivial) |
| (XI) | 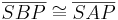
|
(WSW), (X), (IX), (IV) |
| (XII) | 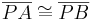
|
(XI), (Def. Dreieckskongruenz) |
-->Beh wahr. qed
Somit ist die Äquivalenz gezeigt --Löwenzahn 11:35, 17. Jul. 2010 (UTC)

