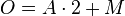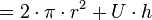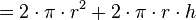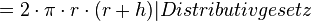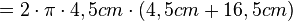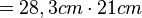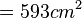Benutzer:HenrikOchel: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Hi, ich bin Henrik, ich studiere an der Pädagogischen Hochschule Heidelberg Lehramt Primarstufe und nutze über die Vorlesung Geometrie Primarstufe das Geomet…“)
 
 
(2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 1: Zeile 1:
 
Hi, ich bin Henrik, ich studiere an der Pädagogischen Hochschule Heidelberg Lehramt Primarstufe und nutze über die Vorlesung Geometrie Primarstufe das Geometrie-Wiki.
 
Hi, ich bin Henrik, ich studiere an der Pädagogischen Hochschule Heidelberg Lehramt Primarstufe und nutze über die Vorlesung Geometrie Primarstufe das Geometrie-Wiki.
 +
 +
[[Datei:Wasserflasche.jpeg|thumb|Dies ist eine Wasserflasche]]
 +
 +
Diese Wasserflasche kann näherungsweise als Zylinder beschrieben werden.
 +
 +
Dieser Zylinder besteht aus einer kreisförmigen Grundfläche mit Radius
 +
 +
<math>r=4,5cm</math>
 +
 +
und hat eine Höhe bis zur 1000ml-Markierung von
 +
 +
<math>h=16,5cm</math>  .
 +
 +
Das Volumen <math>V</math> lässt sich berechnen aus der Grundfläche <math>A</math> multipliziert mit der Höhe <math>h</math>:
 +
 +
 +
<math>V=A \cdot h</math>
 +
 +
<math>=r^2 \cdot \pi \cdot h</math>
 +
 +
<math>=(4,5cm)^2 \cdot \pi \cdot 16,5cm</math>
 +
 +
<math>=20,25cm^2 \cdot \pi \cdot 16,5cm</math>
 +
 +
<math>=1049,7cm^3</math>    .
 +
 +
 +
Da <math>1cm^3 = 1ml</math>  , 
 +
 +
ergibt das eine Füllmenge von <math>V=1049,7ml</math>  ,
 +
 +
bezieht man die Dicke des Plastiks mit ein, dann kommt man relativ genau auf die <math>V=1000ml</math> , die an der Markierung außen auch angezeigt werden.
 +
 +
 +
Die Oberfläche eines Zylinders ist die Summe aus der Grundfläche <math>A</math> verdoppelt und der Mantelfläche <math>M</math>. Diese wiederum wird aus dem Umfang <math>U</math> der Grundfläche und der Höhe <math>h</math> des Zylinders berechnet.
 +
 +
 +
<math>O = A \cdot 2+M</math>
 +
 +
<math>= 2 \cdot \pi \cdot r^2 + U \cdot h</math>
 +
 +
<math>= 2 \cdot \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h</math>
 +
 +
<math>= 2 \cdot \pi \cdot r \cdot (r+h) |Distributivgesetz</math>
 +
 +
<math>= 2 \cdot \pi \cdot 4,5cm \cdot (4,5cm+16,5cm)</math>
 +
 +
<math>= 28,3cm \cdot 21cm</math>
 +
 +
<math>= 593cm^2</math>

Aktuelle Version vom 25. November 2020, 09:23 Uhr

Hi, ich bin Henrik, ich studiere an der Pädagogischen Hochschule Heidelberg Lehramt Primarstufe und nutze über die Vorlesung Geometrie Primarstufe das Geometrie-Wiki.

Dies ist eine Wasserflasche

Diese Wasserflasche kann näherungsweise als Zylinder beschrieben werden.

Dieser Zylinder besteht aus einer kreisförmigen Grundfläche mit Radius

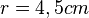
r=4,5cm

und hat eine Höhe bis zur 1000ml-Markierung von

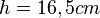h=16,5cm .

Das Volumen 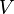V lässt sich berechnen aus der Grundfläche A multipliziert mit der Höhe h:


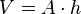
V=A \cdot h

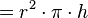
=r^2 \cdot \pi \cdot h

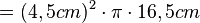
=(4,5cm)^2 \cdot \pi \cdot 16,5cm

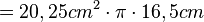
=20,25cm^2 \cdot \pi \cdot 16,5cm

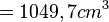=1049,7cm^3 .


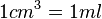Da 1cm^3 = 1ml ,

ergibt das eine Füllmenge von 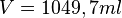V=1049,7ml ,

bezieht man die Dicke des Plastiks mit ein, dann kommt man relativ genau auf die 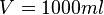V=1000ml , die an der Markierung außen auch angezeigt werden.


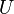Die Oberfläche eines Zylinders ist die Summe aus der Grundfläche A verdoppelt und der Mantelfläche M. Diese wiederum wird aus dem Umfang U der Grundfläche und der Höhe h des Zylinders berechnet.


O = A \cdot 2+M

= 2 \cdot \pi \cdot r^2 + U \cdot h

= 2 \cdot \pi \cdot r^2 + 2 \cdot \pi \cdot r \cdot h

= 2 \cdot \pi \cdot r \cdot (r+h) |Distributivgesetz

= 2 \cdot \pi \cdot 4,5cm \cdot (4,5cm+16,5cm)

= 28,3cm \cdot 21cm

= 593cm^2

Von „http://geometrie.zum.de/index.php?title=Benutzer:HenrikOchel&oldid=36651“