Übungsaufgabe zur Vorbereitung auf die vierte Sitzung: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) |
|||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
# Beweisen Sie den ''Zentriwinkel-Peripheriewinkelsatz'' unter Verwendung der ''Nacheinanderausführung zweier Geradenspiegelungen''. | # Beweisen Sie den ''Zentriwinkel-Peripheriewinkelsatz'' unter Verwendung der ''Nacheinanderausführung zweier Geradenspiegelungen''. | ||
# Erläutern Sie, wie sich Ihr Beweis entsprechend Teilaufgabe 3 vereinfacht, wenn nicht der allgemeine Zentriwinkel-Peripheriewinkelsatz sondern dessen Spezialfall ''Satz des Thales'' zu beweisen ist. | # Erläutern Sie, wie sich Ihr Beweis entsprechend Teilaufgabe 3 vereinfacht, wenn nicht der allgemeine Zentriwinkel-Peripheriewinkelsatz sondern dessen Spezialfall ''Satz des Thales'' zu beweisen ist. | ||
| − | # Wir spielen Billard:<br /> Bei einer Konstellation entsprechend | + | # Wir spielen Billard:<br /> Bei einer Konstellation entsprechend der eingebetteten Geogebraapplikation soll die Kugel A zunächst die Bande c treffen, um dann Kugel B zu erreichen. Geben Sie eine Konstruktionsbeschreibung für die Spur der Kugel A an. Begründen Sie die Korrektheit ihrer Beschreibung. |
# Mike kann es noch besser: Er trifft mit A die Kugel B über die vorherige Berührung erst der Bande c und dann der Bande d. Geben Sie auch hierfür eine Vorschrift zur Konstruktion der Spur von Kugel A an und begründen Sie die Korrektheit ihrer Konstruktionsbeschreibung. | # Mike kann es noch besser: Er trifft mit A die Kugel B über die vorherige Berührung erst der Bande c und dann der Bande d. Geben Sie auch hierfür eine Vorschrift zur Konstruktion der Spur von Kugel A an und begründen Sie die Korrektheit ihrer Konstruktionsbeschreibung. | ||
# Es seien <math>a</math> und <math>b</math> zwei nichtidentische Geraden. Unter <math>S_a</math> und <math>S_b</math> wollen wir wie üblich die Geradenspiegelungen an <math>a</math> bzw. <math>b</math> verstehen. Formulieren Sie die Kontraposition der folgenden Implikation und beweisen sie diese.<br /><math>S_a</math>∘<math>S_b</math>=<math>S_b</math>∘<math>S_a</math>⇒<math>a</math>⊥<math>b</math>. | # Es seien <math>a</math> und <math>b</math> zwei nichtidentische Geraden. Unter <math>S_a</math> und <math>S_b</math> wollen wir wie üblich die Geradenspiegelungen an <math>a</math> bzw. <math>b</math> verstehen. Formulieren Sie die Kontraposition der folgenden Implikation und beweisen sie diese.<br /><math>S_a</math>∘<math>S_b</math>=<math>S_b</math>∘<math>S_a</math>⇒<math>a</math>⊥<math>b</math>. | ||
| + | :: [[Kontraposition und Beispiel zu Nr. 7]] | ||
| + | |||
| + | <ggb_applet width="556" height="508" version="3.2" ggbBase64="UEsDBBQACAAIAEY4+TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3VhLb9w2ED43v4Lgfb16rNwEWDlInIuBtCngJIdeCkoaaxlTpEpS9q5/fYYPaeWti9iFC2R9kjgczeObbzjcXb/ddoLcgDZcyZKmJwklIGvVcNmWdLBXi9f07dmrdQuqhUozcqV0x2xJ85OMOvnAz179sjYbdUuY8CpfOdyW9IoJA5SYXgNrzAbA3pOzYcsFZ3r3qfoGtTX7jWDkQvYDerF6QFndNR+5GZdL77AX3H7gN7wBTYSqS3paYOj49hW05TUTJV0lQZKVNDvYRFHudjdK8zslrVPfG79CCSGG3wF+mTjZeukTXcNQC95wJl0yPg5UIuSWN3ZT0qI4RZPA2w3GuspWwVqtlG4ud8ZCR7Z/glaomDucd2GRFm5hMCp0VyR+Z77yRuDmEqzFohjCtrCHq9W8ube4MO+V2It6xaU9Z70dtK9oHkWXduccoC/twn0nWwFRliHgG6ivK7W99BCkeTD9edf7T3xAVXuuhNJEO3ALVIjPKjy9jot00kq8TuI1og1ndNpP32Rewz+r8PRagssQWsw8HbNOk9ENN8QJHIxIxCl5wSrAwlIySG4/jgskwHVMNQ0f/D50FXbAnAKTzfS5bK6XB+RZX4OWIAJFJNZ2UIMhN46KwZcPpIGad7gMGxES5sr1BQMI0gZaDWPgoX8CYH43mdPwQLxejkG4GAzGWls8CDAf63JxfWqxR0ranbQnlDTMOqlrBAEdYJdYzwlPqQmbd3+ldDoUlO/vsZOjxiw/3H+QIp5MTPQbhpKxCwTbYbvPs/IGf1PN/VyZRMx8Ith1vTPgqtIDhILaSGTSo0HfFrOAPE6GbONhuCvp4tS93AWB1wkt5Frfe81jfQMmP0Dn/QtB5/X/gs75y8Ime05sPrwIbNL/jE2tuo7JhkjWoaM/lNi1SnpMuLstEJaEs4ewNLQZYZljFGG5Ay8AM9hRFU9hgWMu6rOgXQXtGh8rPFhDCNHxA+UJIYwFmCzeH1t2g9NBgjF+ttr5FH1yMdMi9+Us0jhI99VMn1LNf+ecgdatpkDYc2SzH6yPTOaJ1NzTK4n0+jWya5VNth6TAvwtg44J05x3eNGsuZ3YIxy1L6TF2Q5+Vv5zZF8D9O6u9El+1kwad2MOOrOrwCPBr44L/MUqop9E9POjRr8+LvRH6i9G7i/S1THD3xwX/IfcXxwV+AdX+B9cNR5G9Se7aZyO/bB61vv7S4AmH6EpngrNcv470f8xEv8ZOvsOUEsHCFzFLuOiAwAASxIAAFBLAQIUABQACAAIAEY4+TxcxS7jogMAAEsSAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAA3AMAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "true" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "false" allowRescaling = "true" /> | ||
| + | [[Category:Elementargeometrie]] | ||
Aktuelle Version vom 16. November 2010, 22:53 Uhr
- Definieren Sie die Begriffe Zentriwinkel und Peripheriewinkel.
- Formulieren Sie den Zentriwinkel-Peripheriewinkelsatz in der Wenn-Dann-Form.
- Beweisen Sie den Zentriwinkel-Peripheriewinkelsatz unter Verwendung der Nacheinanderausführung zweier Geradenspiegelungen.
- Erläutern Sie, wie sich Ihr Beweis entsprechend Teilaufgabe 3 vereinfacht, wenn nicht der allgemeine Zentriwinkel-Peripheriewinkelsatz sondern dessen Spezialfall Satz des Thales zu beweisen ist.
- Wir spielen Billard:
Bei einer Konstellation entsprechend der eingebetteten Geogebraapplikation soll die Kugel A zunächst die Bande c treffen, um dann Kugel B zu erreichen. Geben Sie eine Konstruktionsbeschreibung für die Spur der Kugel A an. Begründen Sie die Korrektheit ihrer Beschreibung. - Mike kann es noch besser: Er trifft mit A die Kugel B über die vorherige Berührung erst der Bande c und dann der Bande d. Geben Sie auch hierfür eine Vorschrift zur Konstruktion der Spur von Kugel A an und begründen Sie die Korrektheit ihrer Konstruktionsbeschreibung.
- Es seien
und 
zwei nichtidentische Geraden. Unter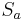 
und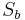 
wollen wir wie üblich die Geradenspiegelungen an bzw. verstehen. Formulieren Sie die Kontraposition der folgenden Implikation und beweisen sie diese.∘=∘⇒⊥.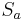
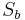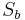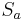