Lösung von Aufgabe 1.4 (SoSe 22): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
Kwd077 (Diskussion | Beiträge) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
da die drei Mengen S<sub>1</sub>,S<sub>2</sub>,S<sub>3</sub> gleich sind und jede Menge eine Teilmenge von sich selbst ist, sind sowohl alle drei Mengen als auch ihre Teilmengen idenisch , außerdem ist ein Quadrat immer eine Teilmenge von einem Rechteck | da die drei Mengen S<sub>1</sub>,S<sub>2</sub>,S<sub>3</sub> gleich sind und jede Menge eine Teilmenge von sich selbst ist, sind sowohl alle drei Mengen als auch ihre Teilmengen idenisch , außerdem ist ein Quadrat immer eine Teilmenge von einem Rechteck | ||
[[http://geometrie.zum.de/wiki/Datei:Mengenvergleich_Vierecke_Lösungsvorschlag_Aufgabe]]--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 13:03, 11. Apr. 2022 (CEST) | [[http://geometrie.zum.de/wiki/Datei:Mengenvergleich_Vierecke_Lösungsvorschlag_Aufgabe]]--[[Benutzer:Kwd077|Kwd077]] ([[Benutzer Diskussion:Kwd077|Diskussion]]) 13:03, 11. Apr. 2022 (CEST) | ||
| + | |||
| + | richtige Antwort! gut gemacht c:--[[Benutzer:Matze2000|Matze2000]] ([[Benutzer Diskussion:Matze2000|Diskussion]]) 17:33, 20. Apr. 2022 (CEST) | ||
Aktuelle Version vom 20. April 2022, 16:33 Uhr
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen.
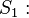Menge aller Vierecke mit vier kongruenten Winkeln
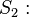Menge aller Vierecke mit gleich langen, einander halbierenden Diagonalen
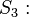Menge aller Vierecke mit zwei Paaren paralleler Gegenseiten und einem rechten Winkel
S1=S2=S3=Rechtecke (inklusive Quadrate)
da die drei Mengen S1,S2,S3 gleich sind und jede Menge eine Teilmenge von sich selbst ist, sind sowohl alle drei Mengen als auch ihre Teilmengen idenisch , außerdem ist ein Quadrat immer eine Teilmenge von einem Rechteck
[[1]]--Kwd077 (Diskussion) 13:03, 11. Apr. 2022 (CEST)
richtige Antwort! gut gemacht c:--Matze2000 (Diskussion) 17:33, 20. Apr. 2022 (CEST)
