Auftrag der Woche5 EG (2010): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | ==Aufgabe | + | ==Aufgabe== |
Es seien <math>\ (x_A, y_A)</math> die Koordinaten des Punktes <math>\ A</math> im <math>\mathbb{R}^2</math>. | Es seien <math>\ (x_A, y_A)</math> die Koordinaten des Punktes <math>\ A</math> im <math>\mathbb{R}^2</math>. | ||
Man beweise: | Man beweise: | ||
| − | Das Bild von <math>\ A</math> bei der Drehung um den Koordinatenursprung mit dem Drehwinkel <math>\ - \alpha</math> hat die Koordinaten <math>\( x_A cos | + | Das Bild von <math>\ A</math> bei der Drehung um den Koordinatenursprung mit dem Drehwinkel <math>\ - \alpha</math> hat die Koordinaten <math>\ ( x_A \cos \alpha +y_A \sin \alpha, -x_A \sin \alpha + y_A \cos \alpha )</math> |
Aktuelle Version vom 30. November 2010, 14:09 Uhr
Aufgabe
Es seien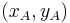 
die Koordinaten des Punktes 
im 
.
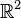Man beweise:
Das Bild von bei der Drehung um den Koordinatenursprung mit dem Drehwinkel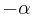 
hat die Koordinaten 
