Lösung von Aufg. 8.7: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 8.5 nicht wahr ist.) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 8.5 nicht wahr ist. | Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 8.5 nicht wahr ist. | ||
| + | |||
| + | <u>Umkehrung:</u><br /> | ||
| + | Wenn der Durchschnitt zweier Punktmengen konvex ist, dann sind die zwei Punktmengen auch konvex.<br /> | ||
| + | die Umkehrung ist korrekt formuliert--[[Benutzer:Schnirch|Schnirch]] 14:24, 14. Dez. 2010 (UTC) | ||
| + | Die Umkehrung stimmt nicht, da es mindestens eine Punktmengen geben kann die nicht konvex ist, aber trotzdem eine Schnittmenge mit der anderen Punktmenge haben kann. --[[Benutzer:Engel82|Engel82]] 18:49, 30. Nov. 2010 (UTC) | ||
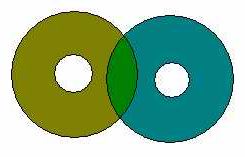
| + | mit der Begründung bin ich nicht ganz einverstanden. Korrekter müsste man sagen: Die Umkehrung stimmt nicht, da unter der Voraussetzung,<br />dass der Schnitt zweier Punktmengen konvex ist, es trotzdem sein kann, dass mind. eine der zwei Punktmengen nicht konvex ist, siehe Beispiel:--[[Benutzer:Schnirch|Schnirch]] 14:24, 14. Dez. 2010 (UTC) | ||
| + | :[[Bild:Donuts 2.jpg]] | ||
| + | |||
| + | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 14. Dezember 2010, 15:24 Uhr
Zeigen Sie mittels einer Skizze, dass die Umkehrung der Implikation aus Aufgabe 8.5 nicht wahr ist.
Umkehrung:
Wenn der Durchschnitt zweier Punktmengen konvex ist, dann sind die zwei Punktmengen auch konvex.
die Umkehrung ist korrekt formuliert--Schnirch 14:24, 14. Dez. 2010 (UTC)
Die Umkehrung stimmt nicht, da es mindestens eine Punktmengen geben kann die nicht konvex ist, aber trotzdem eine Schnittmenge mit der anderen Punktmenge haben kann. --Engel82 18:49, 30. Nov. 2010 (UTC)
mit der Begründung bin ich nicht ganz einverstanden. Korrekter müsste man sagen: Die Umkehrung stimmt nicht, da unter der Voraussetzung,
dass der Schnitt zweier Punktmengen konvex ist, es trotzdem sein kann, dass mind. eine der zwei Punktmengen nicht konvex ist, siehe Beispiel:--Schnirch 14:24, 14. Dez. 2010 (UTC)