Lösung von Aufg. 11.2: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
<u>Kontraposition:</u><br /> | <u>Kontraposition:</u><br /> | ||
Wenn es keine kongruenten Innenwinkel in einem Dreieck ABC gibt, dann ist das Dreieck nicht gleichschenklig.<br /> | Wenn es keine kongruenten Innenwinkel in einem Dreieck ABC gibt, dann ist das Dreieck nicht gleichschenklig.<br /> | ||
| + | ja richtig, die Kontraposition ist eine äquivalente Aussage--[[Benutzer:Schnirch|Schnirch]] 14:00, 25. Jan. 2011 (UTC) | ||
Wenn ein Dreieck gleichschenklig ist, dann sind die Basiswinkel zueinander kongruent.<br /> | Wenn ein Dreieck gleichschenklig ist, dann sind die Basiswinkel zueinander kongruent.<br /> | ||
| + | hier die Konventionaldefinition, auch das ist richtig!--[[Benutzer:Schnirch|Schnirch]] 14:00, 25. Jan. 2011 (UTC) | ||
Gegeben sei ein Dreieck ABC mit <math>\overline{AB}</math> <math>\cong</math> <math>\overline{AC}</math>.<br /> | Gegeben sei ein Dreieck ABC mit <math>\overline{AB}</math> <math>\cong</math> <math>\overline{AC}</math>.<br /> | ||
| − | + | Es gilt: <math>\angle {ABC}\cong</math> <math>\angle {ABC}</math> <br />--[[Benutzer:Engel82|Engel82]] 16:22, 11. Jan. 2011 (UTC) | |
| − | + | auch so kann man es machen!--[[Benutzer:Schnirch|Schnirch]] 14:00, 25. Jan. 2011 (UTC)<br /><br /> | |
| + | Bei der Lösung von Engel82 hat sich in der letzten Zeile ein Fehler eingeschlichen. Der hintere Winkel muss BAC heißen.--[[Benutzer:Jbo-sax|Jbo-sax]] 12:31, 29. Jan. 2011 (UTC)<br /><br /> | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 29. Januar 2011, 13:31 Uhr
Formulieren Sie den Basiswinkelsatz (Satz VII.5) auf zwei weitere Arten und Weisen.
Basiswinkelsatz:
In einem gleichschenkligen Dreieck sind die Basiswinkel zueinander kongruent.
Kontraposition:
Wenn es keine kongruenten Innenwinkel in einem Dreieck ABC gibt, dann ist das Dreieck nicht gleichschenklig.
ja richtig, die Kontraposition ist eine äquivalente Aussage--Schnirch 14:00, 25. Jan. 2011 (UTC)
Wenn ein Dreieck gleichschenklig ist, dann sind die Basiswinkel zueinander kongruent.
hier die Konventionaldefinition, auch das ist richtig!--Schnirch 14:00, 25. Jan. 2011 (UTC)
Gegeben sei ein Dreieck ABC mit 

 .
.
Es gilt: 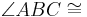
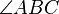
--Engel82 16:22, 11. Jan. 2011 (UTC)
auch so kann man es machen!--Schnirch 14:00, 25. Jan. 2011 (UTC)
Bei der Lösung von Engel82 hat sich in der letzten Zeile ein Fehler eingeschlichen. Der hintere Winkel muss BAC heißen.--Jbo-sax 12:31, 29. Jan. 2011 (UTC)

