Lösung von Aufg. 7.3 (SoSe 11): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“. [[C…“) |
*m.g.* (Diskussion | Beiträge) (→abschließender Kommentar) |
||
| (7 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | == Die Aufgabe == | ||
Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“. | Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“. | ||
| + | ==Lösung von Peterpummel== | ||
| + | Definition komplanar:<br\> | ||
| + | Eine Menge von Punkten <math>M = \{ P_1, P_2, ..., P_n, ..\}</math> heißt komplanar genau dann, wenn eine Ebene E exisitert mit <math>M \subseteq E</math>--[[Benutzer:Peterpummel|Peterpummel]] 12:22, 23. Mai 2011 (CEST)<br /><br /> | ||
| + | korrekt--[[Benutzer:*m.g.*|*m.g.*]] 13:58, 20. Jun. 2011 (CEST) | ||
| + | ==Lösung von LilPonsho== | ||
| + | Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. | ||
| + | Schreibweise: komp(A,B,C,...) | ||
| + | nkomp(A,B,C,...) für nicht komplanar | ||
| + | --LilPonsho 19:09, 7. Jun. 2011 (CEST)<br /><br /> | ||
| + | korrekt--[[Benutzer:*m.g.*|*m.g.*]] 13:58, 20. Jun. 2011 (CEST) | ||
| + | ---- | ||
| + | ==abschließender Kommentar== | ||
| + | Beide Definitionen sind korrekt. | ||
| + | Weitere Variante: | ||
| + | |||
| + | Definition: (komplanar)<br /> | ||
| + | ::Eine Menge <math>M</math> von Punkten heißt komplanar, wenn es eine Ebene <math>\varepsilon</math>gibt, die durch alle Punkte der Menge <math>M</math> geht. | ||
| + | |||
| + | oder | ||
| + | |||
| + | Definition: (komplanar) | ||
| + | ::Es sei <math>M = \left \{ P_1, P_2, ..., P_n, ...\right \}</math> eine Punktmenge. | ||
| + | ::<math>\operatorname{komp}\left ( P_1, P_2, P_n, ... \right ) :\Leftrightarrow P_1 \in \varepsilon, P_2 \in \varepsilon, ... , P_n \in \varepsilon, ....</math> | ||
| + | :: <math>\operatorname{komp}\left ( P_1, P_2, P_n, ... \right )</math> spricht man: <math>\ P_1, P_2, ..., P_n , ...</math> sind komplanar. | ||
| + | --[[Benutzer:*m.g.*|*m.g.*]] 13:52, 20. Jun. 2011 (CEST) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 20. Juni 2011, 13:07 Uhr
Inhaltsverzeichnis |
Die Aufgabe
Die Eigenschaft der Komplanarität ist das räumliche Analogon zur Kollinearität in der Ebene. Formulieren Sie eine Definition der Relation „komplanar“.
Lösung von Peterpummel
Definition komplanar:
Eine Menge von Punkten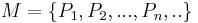 
heißt komplanar genau dann, wenn eine Ebene E exisitert mit 
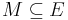--Peterpummel 12:22, 23. Mai 2011 (CEST)
korrekt--*m.g.* 13:58, 20. Jun. 2011 (CEST)
Lösung von LilPonsho
Eine Menge von Punkten heißt komplanar, wenn es eine Ebene gibt, die alle Punkte der Menge enthält. Schreibweise: komp(A,B,C,...)
nkomp(A,B,C,...) für nicht komplanar
--LilPonsho 19:09, 7. Jun. 2011 (CEST)
korrekt--*m.g.* 13:58, 20. Jun. 2011 (CEST)
abschließender Kommentar
Beide Definitionen sind korrekt.
Weitere Variante:
Definition: (komplanar)
- Eine Menge
von Punkten heißt komplanar, wenn es eine Ebene 
gibt, die durch alle Punkte der Menge geht.
- Eine Menge
oder
Definition: (komplanar)
- Es sei
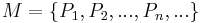eine Punktmenge.
-
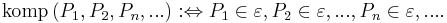
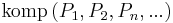spricht man: 
sind komplanar.
- Es sei
--*m.g.* 13:52, 20. Jun. 2011 (CEST)
