Lösung von Aufg. 8.3 (SoSe 11): Unterschied zwischen den Versionen
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 71: | Zeile 71: | ||
Hier noch ein Beweis: | Hier noch ein Beweis: | ||
| − | VSS: nkomp (A,B,C,D), A,B,C,D liegen nicht auf einer Ebene | + | VSS: nkomp (A,B,C,D), A,B,C,D liegen nicht auf einer Ebene (eine der beiden formulierungen genügt, da sie ja das gleiche bedeuten!)<br /> |
| − | BEH: <math>A\neq B\neq C\neq D\neq A</math> | + | BEH: <math>A\neq B\neq C\neq D\neq A</math><br /> |
| − | Annahme: o.B.d.A. | + | Annahme: o.B.d.A. <math>A\equiv B</math><br /> |
| − | <math>A\equiv B</math> | + | |
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 82: | Zeile 81: | ||
| 1 || A = B || Annahme | | 1 || A = B || Annahme | ||
|- | |- | ||
| − | | 2 || nkoll (A, C, D) || Satz aus Übung 7, Nr.6|- | + | | 2 || nkoll (A, C, D) || Satz aus Übung 7, Nr.6 |
| + | |- | ||
| 3 || Die Punkte A, C, D spannen eine Ebene auf || Axiom 1/4 | | 3 || Die Punkte A, C, D spannen eine Ebene auf || Axiom 1/4 | ||
|- | |- | ||
| Zeile 89: | Zeile 89: | ||
| 5 || Widerspruch zur VSS, Annahme ist zu verwerfen, Behauptung stimmt || (4) | | 5 || Widerspruch zur VSS, Annahme ist zu verwerfen, Behauptung stimmt || (4) | ||
|} | |} | ||
| − | --[[Benutzer:Herbst2010|Herbst2010]] 14:27, 8. Jun. 2011 (CEST) | + | --[[Benutzer:Herbst2010|Herbst2010]] 14:27, 8. Jun. 2011 (CEST)<br /> |
| + | Der Ansatz ist gut! Aber Schritt 4 entspricht dem Schritt 3 und es gibt nirgends einen Widerspruch! Hast du die Punkte falsch bezeichnet? --[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:13, 11. Jun. 2011 (CEST) | ||
| + | |||
| + | ==Lösungen der Gruppenarbeit aus der Übung Klara Buchner== | ||
| + | * Die [[Media:Gruppenlösung8.3.jpg|Lösung]] stimmt im Prinzip (wenn die roten Verbesserungen beachtet werden). Versuchen Sie doch, die Lösung nochmal ordentlicher aufzuschreiben. | ||
| + | |||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 21. Juni 2011, 09:24 Uhr
Beweisen Sie: Je vier nicht komplanare Punkte sind paarweise verschieden (Hinweis: Nutzen Sie bei der Beweisführung den Satz aus Aufgabe 7.6).
Voraussetzung: nkomp (A, B, C, D)
Behauptung: A  B
B  C
C  A
A
Aufgrund der Tatsache, dass wir aus Satz 7.6 wissen, dass keine drei Punkte kollinear sind, wenn vier Punkte (A, B, C, D) nicht komplanar sind, müssen wir nur zeigen, dass keine zwei Punkte identisch sind.
Beweis:
Annahme: A = B (o.B.d.A.)
| Nummer | Beweisschritt | Begründung |
| 1 | Es exisitert eine Gerade g mit A  g und B g und B  g g |
Axiom I.1 |
| 2 | A = B | Annahme |
| 3 | Für A = B benötigt die Gerade einen weiteren Punkt, um nach den Inzidenzaxiomen existieren zu können => C  g g |
Axiom I.2, (2) |
| 4 | koll(A, B, C) | (3), Def. kollinear |
| 5 | Widerspruch zur Voraussetzung | (4), Satz 7.6, Voraussetzung |
| 6 | Annahme ist zu verwerfen | (5) |
--Flo60 22:54, 31. Mai 2011 (CEST)
Müsste es nicht bei 5.) komp (A,B,C,D) aus 2.), 4.) und Def. komplanar heißen und somit ein Widerspruch zu der Vor Aufgabe 8.3 sein?--Vollyschwamm 11:55, 1. Jun. 2011 (CEST)
Nein muss es nicht, denn daraus, dass eine Menge von Punkten kollinear ist, folgt nicht automatisch, dass die Punkte auch in jedem Falle komplanar sind. Natürlich gibt es dann eine Ebene, zu der diese Punkte komplanar sind, wir wissen jedoch nicht, ob das genau die Ebene ist, die wir betrachten. Ich habe das mal im Powerpoint gezeichnet. Eine Ebene ist zwar nicht Dreidimensional und auf den Geraden sind keine Punkte eingezeichnet, jeodch ist sicherlich erkennbar, dass alle Punkte auf der Geraden g komplanar zur Ebene sind, weil g vollständig in E ist, während h die Ebene nur schneidet und aber trotzdem alle Punkte auf h kollinear sind.
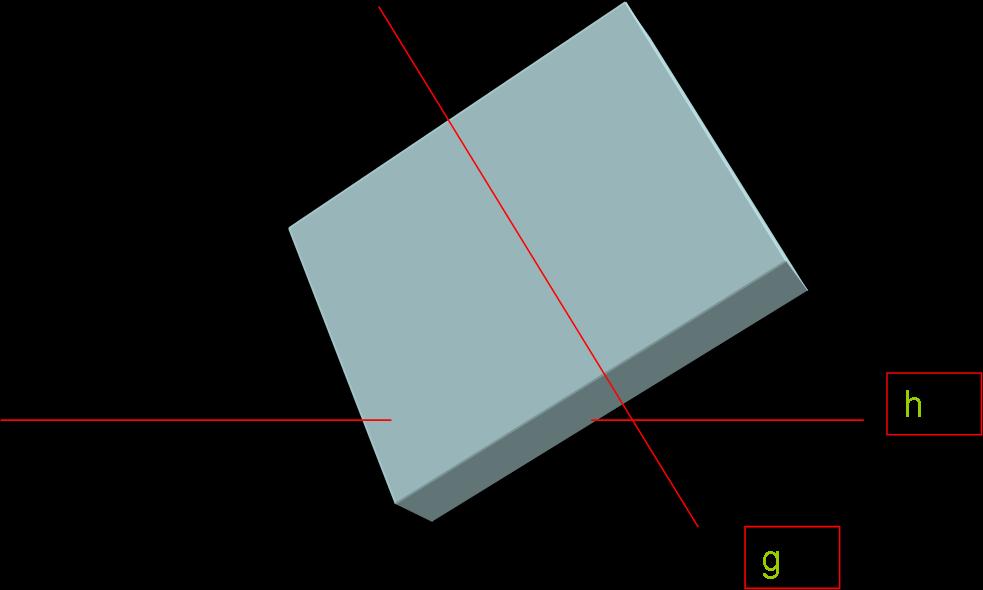 --Flo60 21:38, 1. Jun. 2011 (CEST)
--Flo60 21:38, 1. Jun. 2011 (CEST)
In Schritt 3 haben Sie angenommen, dass es noch einen weiteren Punkt auf der Geraden geben muss.
Das ist korrekt, allerdings muss das nicht zwangsläufig Punkt C oder D sein, sondern z.B.
auch ein neuer Punkt F. Denken Sie an dieser Stelle nochmal über Ihren Beweis nach,
Sie wissen doch noch etwas mehr über Ihre restlichen Punkte, oder?--Schnirch 16:35, 2. Jun. 2011 (CEST)
Neuer Versuch:
Beweis:
Annahme: A = B (o.B.d.A.)
| Nummer | Beweisschritt | Begründung |
| 1 | A = B | Annahme |
| 2 | Es exisitert eine Gerade g mit A  g und B g und B  g und C g und C  g g |
Axiom I.1, (1) |
| 3 | koll(A, B, C) | (3), Def. kollinear |
| 4 | Widerspruch zur Voraussetzung | (4), Satz 7.6, Voraussetzung |
| 5 | Annahme ist zu verwerfen | (5) |
Wenn wir den "Spieß umdrehen" und gleich annehmen, dass A gleich B ist, dann wissen wir auch, dass es eine Gerade gibt, die durch unseren (und nur durch UNSEREN) Punkt C geht. Natürlich gibt es durch die Punkte A und B noch unendlich andere Geraden aber eine geht dann eben durch C und egal ob jetzt C auch noch identisch ist mit A und B oder nicht, das spielt keine Rolle, da wir ja so oder so die Kollinearität der drei Punkt haben, was de facto Widerspruch zu Satz 7.6 ist.
Aber macht es wirklich einen Unterschied? Denn ich habe ja bereits oben "irgendeinen Punkt C" in meiner Vorraussetzung und keinen "Punkt C mit (1|1)" und wenn ich oben irgendeinen Punkt C habe, dann habe ich quasi unten auch "irgendeinen" und somit genau den Punkt C. Das ist so ähnlich wie unendlich ist unendlich (Strecke AB mit d  0 hat genauso viele unendliche Punkte wie die Ebene in der sie als Teilmenge (!) enthalten ist) - irgendeiner ist irgendeiner :-) aber wahrscheinlich halt nicht.
0 hat genauso viele unendliche Punkte wie die Ebene in der sie als Teilmenge (!) enthalten ist) - irgendeiner ist irgendeiner :-) aber wahrscheinlich halt nicht.
--Flo60 18:04, 2. Jun. 2011 (CEST)
Den Beweis kann ich nachvollziehen, aber den Kommentar bzw. die Erläuterung muss ich mir nochmal zu Gemüte führen :) --Tutor Andreas 11:53, 4. Jun. 2011 (CEST)
Hier noch ein Beweis:
VSS: nkomp (A,B,C,D), A,B,C,D liegen nicht auf einer Ebene (eine der beiden formulierungen genügt, da sie ja das gleiche bedeuten!)
BEH: 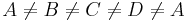
Annahme: o.B.d.A. 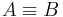
| Nummer | Beweisschritt | Begründung |
| 1 | A = B | Annahme |
| 2 | nkoll (A, C, D) | Satz aus Übung 7, Nr.6 |
| 3 | Die Punkte A, C, D spannen eine Ebene auf | Axiom 1/4 |
| 4 | A, C, D  der Ebene der Ebene |
(2), (3) |
| 5 | Widerspruch zur VSS, Annahme ist zu verwerfen, Behauptung stimmt | (4) |
--Herbst2010 14:27, 8. Jun. 2011 (CEST)
Der Ansatz ist gut! Aber Schritt 4 entspricht dem Schritt 3 und es gibt nirgends einen Widerspruch! Hast du die Punkte falsch bezeichnet? --Tutorin Anne 11:13, 11. Jun. 2011 (CEST)
Lösungen der Gruppenarbeit aus der Übung Klara Buchner
- Die Lösung stimmt im Prinzip (wenn die roten Verbesserungen beachtet werden). Versuchen Sie doch, die Lösung nochmal ordentlicher aufzuschreiben.

