Lösung von Aufg. 12.4 SS11: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „Beweisen Sie Satz VII.6 b ::Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <mat…“)
 
 
(2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt)
Zeile 2: Zeile 2:
  
 
::Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand.
 
::Wenn ein Punkt <math>\ P</math> zur Mittelsenkrechten der Strecke <math>\overline{AB}</math> gehört, dann hat er zu den Punkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand.
 +
 +
 +
<math>\ Beweis: </math>
 +
 +
<math> \ Voraussetzung :\ m \ ist \ Mittelsenkrechte \ von \ \overline{AB} \  und \ P \in m </math> <br>
 +
<math> \ Behauptung: \ \overline{PA} \equiv \overline{BP} </math> <br>
 +
 +
<math> \ Es \ gilt \ : \ </math> <br>
 +
 +
<math>\overline{PM} \equiv \overline{PM} \ und \ \angle PMA \equiv \angle PBM \ und \ \overline{AM} \equiv \overline{BM} \ nach \ Voraussetzung </math><br>
 +
<math>\Rightarrow \ Kongruenz \ von \ \overline{APM} \ und \  \overline{PMB}\Rightarrow \overline{AP} \equiv \overline{BP}</math>
 +
--[[Benutzer:Peterpummel|Peterpummel]] 18:06, 3. Jul. 2011 (CEST)
 +
 +
 +
Muss das auch für P = M gezeigt werden? Oder ist das einfach trivial, weil P dann Mittelpunkt ist und logischerweise
 +
zu A und B denselben Abstand hat?--[[Benutzer:Mm l123|mm_l]] 10:45, 15. Jul. 2011 (CEST)<br /><br />
 +
 +
Ja, trotz das der Beweis für P=M trivial ist, muss man diesen Fall getrennt aufführen, denn es enstechen ja keine Dreicke!<br /> Das heißt, für ein korrekten Beweis muss man hier in zwei Fälle unterscheiden. (vgl. Aufgabe 12.3)--[[Benutzer:Tutorin Anne|Tutorin Anne]] 10:37, 17. Jul. 2011 (CEST)

Aktuelle Version vom 17. Juli 2011, 09:37 Uhr

Beweisen Sie Satz VII.6 b

Wenn ein Punkt \ P zur Mittelsenkrechten der Strecke \overline{AB} gehört, dann hat er zu den Punkten \ A und \ B ein und denselben Abstand.


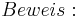
\ Beweis:

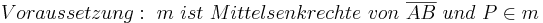
\ Voraussetzung :\ m \ ist \ Mittelsenkrechte \ von \ \overline{AB} \ und \ P \in m
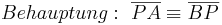
\ Behauptung: \ \overline{PA} \equiv \overline{BP}

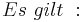
\ Es \ gilt \ : \

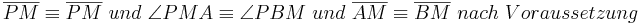
\overline{PM} \equiv \overline{PM} \ und \ \angle PMA \equiv \angle PBM \ und \ \overline{AM} \equiv \overline{BM} \ nach \ Voraussetzung
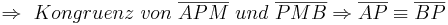\Rightarrow \ Kongruenz \ von \ \overline{APM} \ und \ \overline{PMB}\Rightarrow \overline{AP} \equiv \overline{BP} --Peterpummel 18:06, 3. Jul. 2011 (CEST)


Muss das auch für P = M gezeigt werden? Oder ist das einfach trivial, weil P dann Mittelpunkt ist und logischerweise zu A und B denselben Abstand hat?--mm_l 10:45, 15. Jul. 2011 (CEST)

Ja, trotz das der Beweis für P=M trivial ist, muss man diesen Fall getrennt aufführen, denn es enstechen ja keine Dreicke!
Das heißt, für ein korrekten Beweis muss man hier in zwei Fälle unterscheiden. (vgl. Aufgabe 12.3)--Tutorin Anne 10:37, 17. Jul. 2011 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufg._12.4_SS11&oldid=8261“