Lösung von Aufg. 9.6 (WS 11/12): Unterschied zwischen den Versionen
RicRic (Diskussion | Beiträge) |
|||
| Zeile 3: | Zeile 3: | ||
Bei dem Halbraum <math>\epsilon\ Q^{+}</math> handelt es sich um die Vereinigung der Punkte von der Ebene <math>\epsilon</math> mit allen Punken für die gilt, dass sie Strecke zu dem Punkt <math>Q</math> geschnitten mit der Ebene <math>\epsilon</math> die leere Menge ist.<br /> | Bei dem Halbraum <math>\epsilon\ Q^{+}</math> handelt es sich um die Vereinigung der Punkte von der Ebene <math>\epsilon</math> mit allen Punken für die gilt, dass sie Strecke zu dem Punkt <math>Q</math> geschnitten mit der Ebene <math>\epsilon</math> die leere Menge ist.<br /> | ||
| − | Bei dem Halbraum <math>\epsilon\ Q^{-}</math> handelt es sich um alle Punkte die nicht dem Halbraum <math>\epsilon\ Q^{+}</math> angehören vereinigt mit allen Punkte der Ebene <math>\epsilon</math>.--[[Benutzer:RicRic|RicRic]] 22:22, 8. Dez. 2011 (CET) | + | Bei dem Halbraum <math>\epsilon\ Q^{-}</math> handelt es sich um alle Punkte die nicht dem Halbraum <math>\epsilon\ Q^{+}</math> angehören vereinigt mit allen Punkte der Ebene <math>\epsilon</math>.--[[Benutzer:RicRic|RicRic]] 22:22, 8. Dez. 2011 (CET)<br /> |
| + | Gut!<br /> Eine Kleinigkeit vielleicht -die Formulierung scheint mir so besser:<br /> | ||
| + | Bei dem Halbraum <math>\epsilon\ Q^{+}</math> handelt es sich um die Vereinigung der Punkte <s>von</s> der Ebene <math>\epsilon</math> mit allen Punken <math>P</math> für die gilt, dass die Strecke <math>\overline{PQ}</math> geschnitten mit der Ebene <math>\epsilon</math> die leere Menge ist.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:02, 14. Dez. 2011 (CET)<br /> | ||
| + | |||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Aktuelle Version vom 14. Dezember 2011, 14:02 Uhr
Unter dem Raum 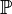 versteht man die Menge aller Punkte. Die Punktmenge
versteht man die Menge aller Punkte. Die Punktmenge
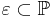 sei eine Ebene. Gegeben sei ferner
sei eine Ebene. Gegeben sei ferner  mit
mit 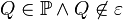 . Definieren Sie die Begriffe Halbraum
. Definieren Sie die Begriffe Halbraum 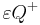 und
und 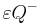 .
.
Bei dem Halbraum 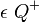 handelt es sich um die Vereinigung der Punkte von der Ebene
handelt es sich um die Vereinigung der Punkte von der Ebene  mit allen Punken für die gilt, dass sie Strecke zu dem Punkt
mit allen Punken für die gilt, dass sie Strecke zu dem Punkt  geschnitten mit der Ebene
geschnitten mit der Ebene  die leere Menge ist.
die leere Menge ist.
Bei dem Halbraum 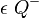 handelt es sich um alle Punkte die nicht dem Halbraum
handelt es sich um alle Punkte die nicht dem Halbraum 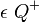 angehören vereinigt mit allen Punkte der Ebene
angehören vereinigt mit allen Punkte der Ebene  .--RicRic 22:22, 8. Dez. 2011 (CET)
.--RicRic 22:22, 8. Dez. 2011 (CET)
Gut!
Eine Kleinigkeit vielleicht -die Formulierung scheint mir so besser:
Bei dem Halbraum 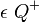 handelt es sich um die Vereinigung der Punkte
handelt es sich um die Vereinigung der Punkte von der Ebene  mit allen Punken
mit allen Punken  für die gilt, dass die Strecke
für die gilt, dass die Strecke  geschnitten mit der Ebene
geschnitten mit der Ebene  die leere Menge ist.--Tutorin Anne 14:02, 14. Dez. 2011 (CET)
die leere Menge ist.--Tutorin Anne 14:02, 14. Dez. 2011 (CET)

